基于IDA方法的高层剪力墙结构抗震能力影响因素分析

孙柏涛; 张博; 闫培雷

doi:10.11899/zzfy20180412

基于IDA方法的高层剪力墙结构抗震能力影响因素分析

doi: 10.11899/zzfy20180412

孙柏涛^{1, 2,},
张博^{1, 2, ,},
闫培雷^{1, 2}

1.
中国地震局工程力学研究所, 哈尔滨 150080
2.
中国地震局地震工程与工程振动重点实验室, 哈尔滨 150080

基金项目:

国家自然科学青年基金项目 51708524

国家自然科学青年基金项目 51608495

详细信息

作者简介:
孙柏涛, 男, 生于1961年。研究员。主要从事地震灾害评估等方面的研究。E-mail:sunbt@iem.cn

通讯作者:
张博, 男, 生于1991年。硕士研究生。主要从事剪力墙结构抗震性能方面的研究。E-mail:bsmilezhang@126.com

计量
- 文章访问数: 146
- HTML全文浏览量: 13
- PDF下载量: 9
- 被引次数: 0
出版历程
- 收稿日期: 2018-03-15
- 刊出日期: 2018-12-01

Analysis of Influencing Factors of Seismic Capability of High-rise Shear Wall Structure by Using Incremental Dynamic Method

Sun Baitao^{1, 2
,},
Zhang Bo^{1, 2
, ,},
Yan Peilei^{1, 2}

1.
Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China
2.
Key Laboratory of Earthquake Engineering and Engineering Vibration, China Earthquake Administration, Harbin 150080, China

摘要

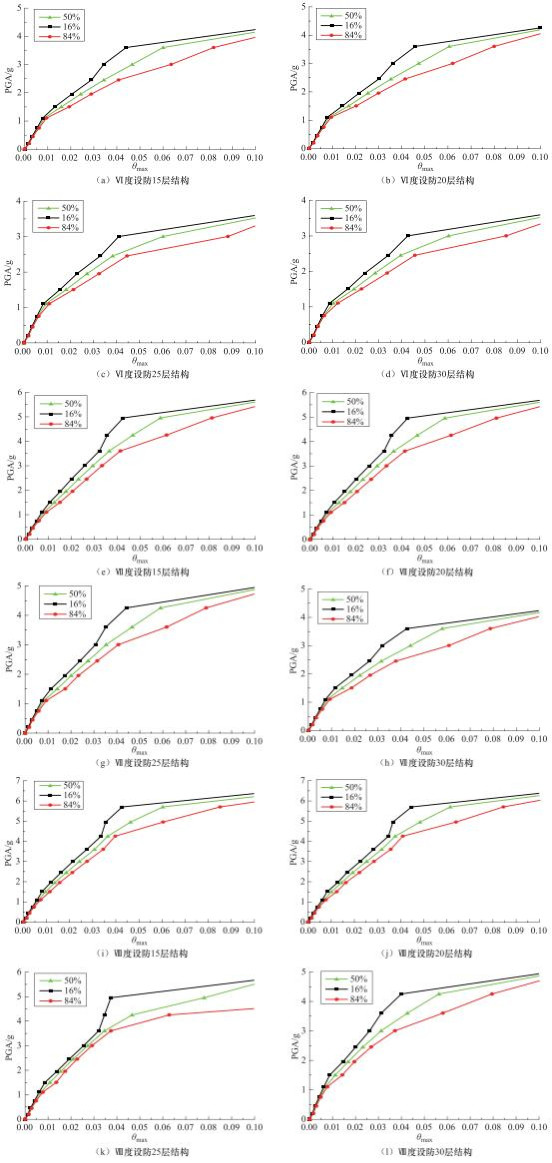
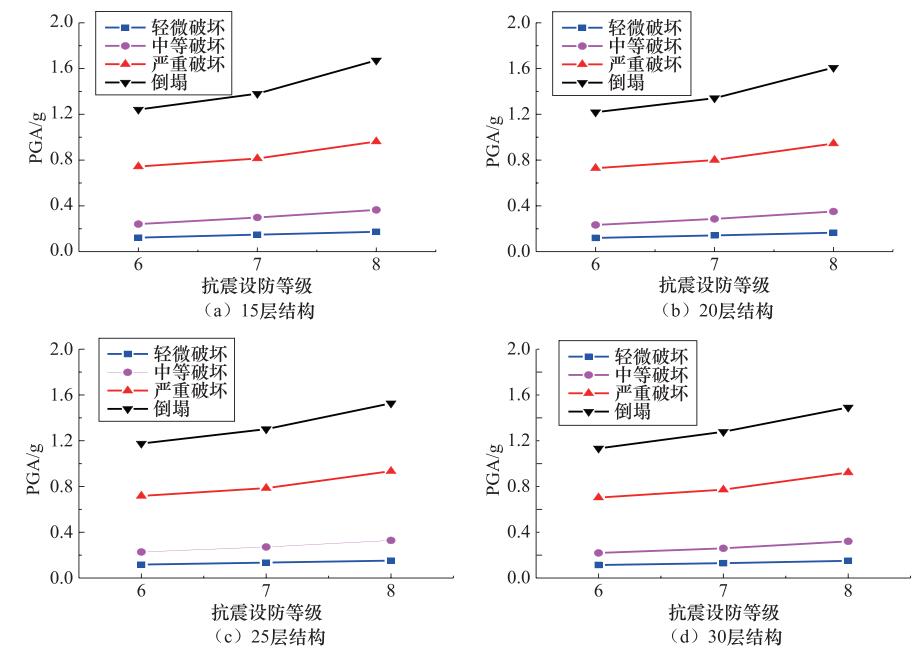
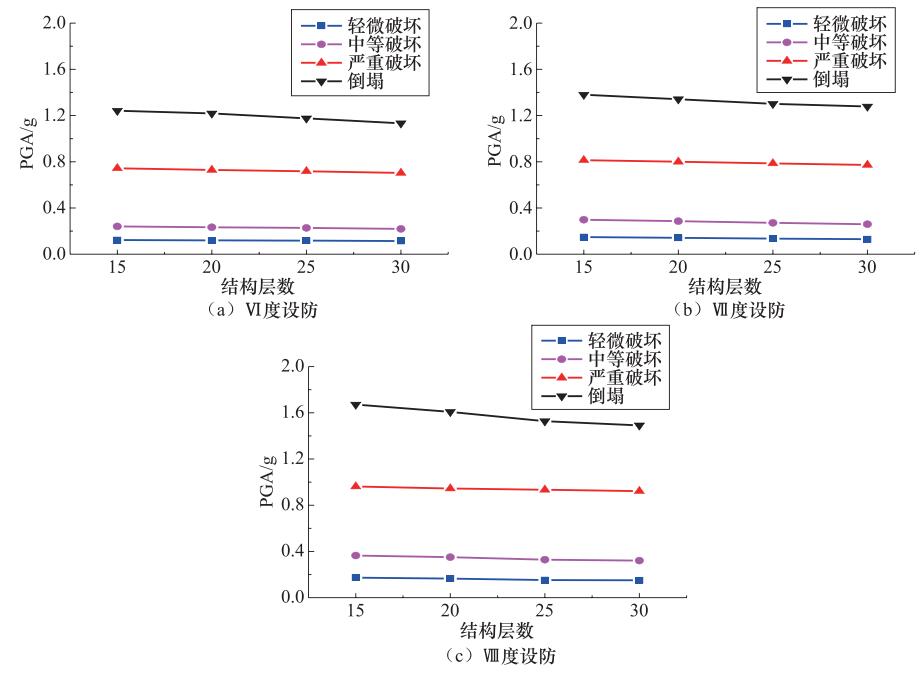
摘要: 介绍了IDA方法的基本原理和分析步骤，采用Etabs软件对12个不同设防烈度、不同层数的高层剪力墙结构进行增量动力分析，给出了各结构模型在不同性能水平的最大层间位移角，并探讨了抗震设防等级和高度对剪力墙结构抗震能力的影响。研究表明，随着抗震设防等级的提高，结构的抗震能力会有显著的提升，而随着结构高度的增加，结构的抗震能力会相应降低。
- 增量动力分析 /
- 抗震能力 /
- 抗震设防等级 /
- 结构高度
Abstract: The basic principles and analytical steps of the IDA method are introduced in this paper. The Etabs software is used to perform incremental dynamic analysis on 12 high-rise shear wall structures with different fortification intensities and different layers, and the maximum layers of each structural model at different performance levels are given. The maximum inter-layer displacement angles of various structural models at different performance levels are given, and the influence of seismic fortification grade and height on the seismic performance of shear wall structures is discussed. Our results show that with the increase of seismic fortification level, the seismic capacity of the structure is significantly improved, and with the increase of the structure height, the seismic resistance of the structure is reduced accordingly. This conclusion is useful in providing a strong scientific basis for studying the earthquake damage and loss of engineering structures.
- Incremental dynamic analysis /
- The seismic capacity /
- Earthquake resistance level /
- Structure height

HTML全文

图 1 结构平面布置

Figure 1. The plan layout of structure

下载: 全尺寸图片幻灯片

图 2 IDA曲线

Figure 2. IDA curves of the structure

下载: 全尺寸图片幻灯片

图 3 各破坏性能点随抗震设防等级变化的规律

Figure 3. The regular graph of the failed performance point varying with the earthquake resistance level

下载: 全尺寸图片幻灯片

图 4 各破坏性能点随结构高度变化的规律

Figure 4. The regular graph of the failed performance point varying with the structure height

下载: 全尺寸图片幻灯片

表 1 最不利设计地震动详细信息

Table 1. The detailed information of the most unfavorable design ground vibration

编号	震级	年份	地点	断层距/km	PGA/g
F2	6.69	1994	北岭	54.45	0.154
F3	6.61	1971	圣费尔南多	22.63	0.32
F4	5.01	1979	帝王谷#10	12.96	0.054
F5	7.36	1952	克恩县	38.89	0.18
F7	6.95	1940	埃尔森特罗	6.09	0.281
F10	6.36	1983	科林加	29.48	0.274
F11	6.53	1979	帝王谷#6	1.35	0.449
F12	6.19	1966	帕克菲尔德	12.9	0.272
N1	6.7	1988	澜沧	17.6	0.207
N4	7.8	1976	宁河	67	0.15

下载: 导出CSV

表 2 量化指标限值

Table 2. Limits of the quantitative indicators

破坏等级	基本完好	轻微破坏	中等破坏	严重破坏	倒塌
最大层间位移角θ_max	＜1/950	1/950—1/500	1/500—1/175	1/175—1/90	＞1/90

下载: 导出CSV

表 3 结构各破坏状态对应的能力值（50%分位曲线）

Table 3. The corresponding ability value of each failure state of the structure

模型	轻微破坏		中等破坏		严重破坏		倒塌
模型	θ_max	PGA/g	θ_max	PGA/g	θ_max	PGA/g	θ_max	PGA/g
Ⅵ度15层	0.00105	0.1222	0.002	0.2402	0.00571	0.7437	0.01111	1.242
Ⅵ度20层		0.1195		0.2331		0.7289		1.218
Ⅵ度25层		0.1174		0.2274		0.718		1.1753
Ⅵ度30层		0.114		0.2191		0.7029		1.1328
Ⅶ度15层		0.1483		0.2981		0.8138		1.3803
Ⅶ度20层		0.1417		0.2857		0.8006		1.3413
Ⅶ度25层		0.1348		0.2713		0.7858		1.3014
Ⅶ度30层		0.1297		0.2592		0.7725		1.2784
Ⅷ度15层		0.173		0.3647		0.9619		1.6712
Ⅷ度20层		0.1654		0.3507		0.9449		1.6077
Ⅷ度25层		0.1524		0.3284		0.9342		1.5273
Ⅷ度30层		0.1505		0.3206		0.9223		1.4911

下载: 导出CSV

表 4 结构层数所对应高度

Table 4. The height value corresponding to the number of structural layers

结构层数	15	20	25	30
结构高度/m	41.2	55.2	69.2	83.2

下载: 导出CSV

参考文献(13)

卜一, 吕西林, 周颖等, 2009.采用增量动力分析方法确定高层混合结构的性能水准.结构工程师, 25(2):77-84. doi: 10.3969/j.issn.1005-0159.2009.02.016

邓明科, 梁兴文, 辛力, 2008.剪力墙结构基于性能抗震设计的目标层间位移确定方法.工程力学, 25(11):141-148. http://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200811026.htm

韩建平, 吕西林, 李慧, 2007.基于性能的地震工程研究的新进展及对结构非线性分析的要求.地震工程与工程振动, 27(4):15-23. doi: 10.3969/j.issn.1000-1301.2007.04.003

韩淼, 那国坤, 2011.基于增量动力法的剪力墙结构地震易损性分析.世界地震工程, 27(3):108-113. http://d.old.wanfangdata.com.cn/Periodical/sjdzgc201103016

吕西林, 苏宁粉, 周颖, 2012.复杂高层结构基于增量动力分析法的地震易损性分析.地震工程与工程振动, 32(5):19-25. http://d.old.wanfangdata.com.cn/Periodical/dzgcygczd201205004

汪梦甫, 曹秀娟, 孙文林, 2010.增量动力分析方法的改进及其在高层混合结构地震危害性评估中的应用.工程抗震与加固改造, 32(1):104-109, 121. doi: 10.3969/j.issn.1002-8412.2010.01.019

谢礼立, 翟长海, 2003.最不利设计地震动研究.地震学报, 25(3):250-261. doi: 10.3321/j.issn:0253-3782.2003.03.003

中华人民共和国建设部, 2010.JGJ 3-2010高层建筑混凝土结构技术规程.北京: 中国建筑工业出版社.

中华人民共和国住房和城乡建设部, 2010.GB 50010-2010混凝土结构设计规范.北京: 中国建筑工业出版社.

中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2010.GB 50011-2010建筑抗震设计规范.北京: 中国建筑工业出版社.

中华人民共和国住房和城乡建设部, 2012.GB 50009-2012建筑结构荷载规范.北京: 中国建筑工业出版社.

Federal Emergency Management Agency (FEMA), 2000. Recommended Seismic Design Criteria for New Steel Moment-frame Buildings. FEMA 350, Washington, DC: SAC Joint Venture.

Vamvatsikos D., Cornell C. A., 2002. Incremental dynamic analysis. Earthquake Engineering & Structural Dynamics, 31 (3):491-514. http://d.old.wanfangdata.com.cn/Periodical/tjdxxb201002006

施引文献

资源附件(0)

访问统计