The Application of Differential Quadrature Method in Structural Dynamic Analysis
-
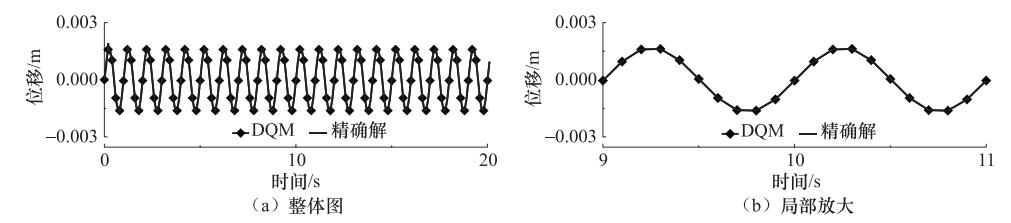
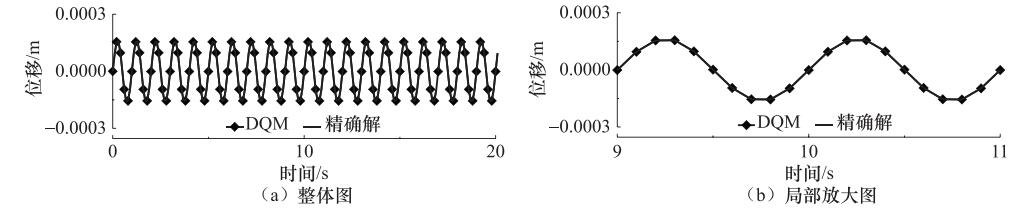
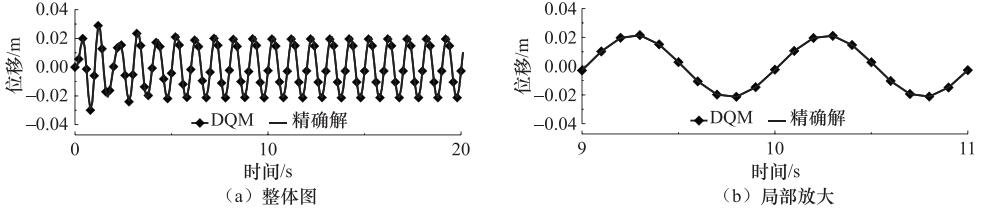
摘要: 微分求积法（DQM）是1种求解微分方程初（边）值问题的数值方法，通常以较小的计算工作量即可获得较高的数值精度。这种方法应用于工程领域时多用来解决梁、板等结构的静力分析或结构特征值分析等问题，即对边值问题的微分方程的求解。结构动力分析属于初值问题，荷载和结构反应都具有特殊性，直接套用DQM求解边值问题并不能获得问题的解。本文尝试利用微分求积原理建立求解结构动力反应的具体方法。借鉴单元法的思想，将荷载持时划分为若干个时步，在每个时步内对动态荷载和结构反应进行离散，然后用DQM对时步逐个进行求解，得到体系在整个时域内的反应过程。通过对3种不同自振周期的线弹性单自由度体系在不同频率简谐激励下反应的计算，阐释了本文方法的可行性以及高精度、高效率的特点，通过数值试验确定了时步内相对较优的节点数，并为时步长度的选取提供了建议。Abstract: The differential quadrature method (DQM) is a numerical technique of solving initial/boundary value problems of differential equations and capable of obtaining a higher numerical accuracy with a smaller calculation workload. This method is often used to solve the problems of structural static analysis of beams and slabs or eigenvalue analysis when it is applied to the engineering fields, which is to solve the differential equation of the boundary value problems. Dynamic analysis of structures is an initial value problem as well as particular loads and structural response. As a result, applying the DQ method of solving the boundary value problem directly cannot obtain solution of problem. The principle of differential quadrature is applied to establish the specific method of solving structural dynamic response in this paper. By analogizing the idea of unit method, the duration of the load is divided into many time steps and dynamic load and structure are discretized in each time step, then the response of the system can be solved in the whole time domain by employing the DQ method step by step. The feasibility of this method and the characteristics of high precision and high efficiency are expounded by calculating the response of three linear elastic single-freedom-degree system of different natural vibration periods excited by simple harmonic loads of different frequencies. By means of numerical experiment, the optimal meshing scheme is determined and the suggestion for the time step is given.
-
图 1 简谐荷载激励下体系1的位移反应
Figure 1. Displacement response of system 1 under simple harmonic load
图 2 简谐荷载激励下体系2的位移反应
Figure 2. Displacement response of system 2 under simple harmonic load
图 3 简谐荷载激励下体系3的位移反应
Figure 3. Displacement response of system 3 under simple harmonic load
表 1 体系的基本特性
Table 1. Basic characteristics of systems
体系编号 自振周期Tn/s 阻尼比ξ 1 0.68 0.05 2 0.25 0.05 3 0.08 0.05 
下载: 导出CSV
表 2 简谐荷载的信息
Table 2. Information of simple harmonic load
荷载函数/N 周期/s 振幅/m 持时/s sin2πt 1 1 40 sin10πt 0.2 1 40 sin20πt 0.1 1 40
下载: 导出CSV
表 3 荷载周期1s的平均相对误差
Table 3. Average relative error with load period of 1s
m 体系编号 1 2 3 位移/% 速度/% 位移/% 速度/% 位移/% 速度/% 2 98.734 98.734 98.734 98.734 98.734 98.734 4 88.218 81.849 99.415 389.850 53.532 1293.500 6 42.402 32.547 15.926 4.728 10.979 9.609 8 6.698 8.020 1.543 7.814 2.042 2.741 10 1.623 2.687 0.907 2.338 1.036 0.349 12 0.121 0.138 0.897 3.341 0.819 4.156 14 0.008 0.009 0.935 5.153 0.716 1.290 16 0 0 0.930 3.899 0.635 0.825 18 0 0 1.005 3.292 0.577 2.28 20 0 0 1.268 4.715 0.527 0.899
下载: 导出CSV
表 4 荷载周期0.2s的平均相对误差
Table 4. Average relative error with load period of 0.2s
m 体系编号 1 2 3 位移/% 速度/% 位移/% 速度/% 位移/% 速度/% 2 99.749 99.749 99.749 99.749 99.749 99.749 4 799.760 2460.400 403.870 411.780 108.540 225.480 6 90.884 11.229 23.620 19.707 11.436 5.439 8 6.052 15.762 2.102 2.135 1.068 2.520 10 0.264 0.046 0.116 0.140 0.765 1.155 12 0.009 0.022 0.005 0.004 0.807 3.325 14 3681.600 256.240 251.760 2935.800 972.740 1334.400 16 0 0 0 0 0.093 0.167 18 0 0 0 0 0.010 0.013 20 0 0 0 0 0.001 0.001
下载: 导出CSV
表 5 荷载周期为0.1s的平均相对误差
Table 5. Average relative error with load period of 0.1 seconds
m 体系编号 1 2 3 位移/% 速度/% 位移/% 速度/% 位移/% 速度/% 2 99.875 99.875 99.875 99.875 99.875 99.875 4 1620.200 1370.200 578.690 459.540 51.868 52.298 6 175.570 9.444 65.345 7.903 6.80×10282 8.63×10282 8 11.571 9.569 4.413 3.254 1.951 2.655 10 0.498 0.046 0.204 0.044 0.142 0.266 12 0.016 0.013 0.007 0.005 0.006 0.007 14 27683 306.960 1322.400 246.430 234.600 3888.600 16 0 0 0 0 0 0 18 0 0 0 0 0 0 20 0 0 0 0 0 0
下载: 导出CSV
-
李鸿晶, 王通, 2011a.结构地震反应分析的逐步微分积分方法.力学学报, 43(2):430-435. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=CAS201303040000629782 李鸿晶, 廖旭, 王通, 2011b.结构地震反应DQ解法的两种数值格式.应用基础与工程科学学报, 19(5):758-766. http://d.old.wanfangdata.com.cn/Periodical/yyjcygckxxb201105008 廖旭, 李鸿晶, 孙广俊, 2013.基于DQ原理的结构弹塑性地震反应分析.工程力学, 30(7):161-166. http://www.cnki.com.cn/Article/CJFDTotal-GCLX201307026.htm 王鑫伟, 1995.微分求积法在结构力学中的应用.力学进展, 25(2):232-240. doi: 10.3321/j.issn:1000-0992.1995.02.010 Bellman R., Casti J., 1971. Differential quadrature and long-term integration. Journal of Mathematical Analysis and Applications, 34 (2):235-238. doi: 10.1016/0022-247X(71)90110-7 Bellman R., Kashef B. G., Casti J., 1972. Differential quadrature:a technique for the rapid solution of nonlinear partial differential equations. Journal of Computational Physics, 10 (1):40-52. doi: 10.1016/0021-9991(72)90089-7 Bert C. W., Jang S. K., Striz A. G., 1988. Two new approximate methods for analyzing free vibration of structural components. AIAA Journal, 26 (5):612-618. doi: 10.2514/3.9941 Bert C. W., Wang X. W., Striz A. G., 1993. Differential quadrature for static and free vibration analyses of anisotropic plates. International Journal of Solids and Structures, 30 (13):1737-1744. doi: 10.1016/0020-7683(93)90230-5 Bert C. W., Malik M., 1996. The differential quadrature method for irregular domains and application to plate vibration. International Journal of Mechanical Sciences, 38 (6):589-606. doi: 10.1016/S0020-7403(96)80003-8 Bert C. W., Malik M., 1997. Differential quadrature:a powerful new technique for analysis of composite structures. Composite Structures, 39 (3-4):179-189. doi: 10.1016/S0263-8223(97)00112-8 Fung T. C., 2001a. Solving initial value problems by differential quadrature method——part 1:first-order equations. International Journal for Numerical Methods in Engineering, 50 (6):1411-1427. doi: 10.1002/(ISSN)1097-0207 Fung T. C., 2001b. Solving initial value problems by differential quadrature method——part 2:second-and higher-order equations. International Journal for Numerical Methods in Engineering, 50 (6):1429-1454. doi: 10.1002/(ISSN)1097-0207 Jang S. K., Bert C. W., Striz A. G., 1989. Application of differential quadrature to static analysis of structural components. International Journal for Numerical Methods in Engineering, 28 (3):561-577. doi: 10.1002/(ISSN)1097-0207 Kang K., Bert C. W., Striz A. G., 1995. Vibration analysis of shear deformable circular arches by the differential quadrature method. Journal of Sound and Vibration, 183 (2):353-360. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cd5d834cd6a527d56839a5876ae0d87a Kang K., Bert C. W., Striz A. G., 1996. Vibration analysis of horizontally curved beams with warping using DQM. Journal of Structural Engineering, 122 (6):657-662. doi: 10.1061/(ASCE)0733-9445(1996)122:6(657) Liew K. M., Han J. B., Xiao Z. M., 1996a. Differential quadrature method for thick symmetric cross-ply laminates with first-order shear flexibility. International Journal of Solids and Structures, 33 (18):2647-2658. doi: 10.1016/0020-7683(95)00174-3 Liew K. M., Han J. B., Xiao Z. M., et al., 1996b. Differential quadrature method for Mindlin plates on Winkler foundations. International Journal of Mechanical Sciences, 38 (4):405-421. doi: 10.1016/0020-7403(95)00062-3 Liu J., Wang X. W., 2008. An assessment of the differential quadrature time integration scheme for nonlinear dynamic equations. Journal of Sound and Vibration, 314 (1-2):246-253. doi: 10.1016/j.jsv.2008.01.004 Newmark N. M., 1959. A method of computation for structural dynamics. Journal of the Engineering Mechanics Division, 85 (3):67-94. http://cn.bing.com/academic/profile?id=04737dd237295d8ef1e115cb61eed609&encoded=0&v=paper_preview&mkt=zh-cn Sherbourne A. N., Pandey M. D., 1991. Differential quadrature method in the buckling analysis of beams and composite plates. Computers & Structures, 40 (4):903-913. doi: 10.1016-0045-7949(91)90320-L/ Striz A. G., Jang S. K., Bert C. W., 1988. Nonlinear bending analysis of thin circular plates by differential quadrature. Thin-Walled Structures, 6 (1):51-62. doi: 10.1016/0263-8231(88)90025-0 Wang X., Bert C. W., Striz A. G., 1993. Differential quadrature analysis of deflection, buckling, and free vibration of beams and rectangular plates. Computers & Structures, 48 (3):473-479. http://cn.bing.com/academic/profile?id=5a95130e65486d67576bb93101054491&encoded=0&v=paper_preview&mkt=zh-cn Wang X., Striz A. G., Bert C. W., 1994. Buckling and vibration analysis of skew plates by the differential quadrature method. AIAA Journal, 32 (4):886-889. doi: 10.2514/3.12071 Zeng H., Bert C. W., 2001. A differential quadrature analysis of vibration for rectangular stiffened plates. Journal of Sound and Vibration, 241 (2):247-252. doi: 10.1006/jsvi.2000.3295 -
点击查看大图
图(3) / 表(5)
计量
- 文章访问数: 51
- HTML全文浏览量: 26
- PDF下载量: 3
- 被引次数: 0
