Study of the Computational Method of Instrumental Seismic Intensity
-
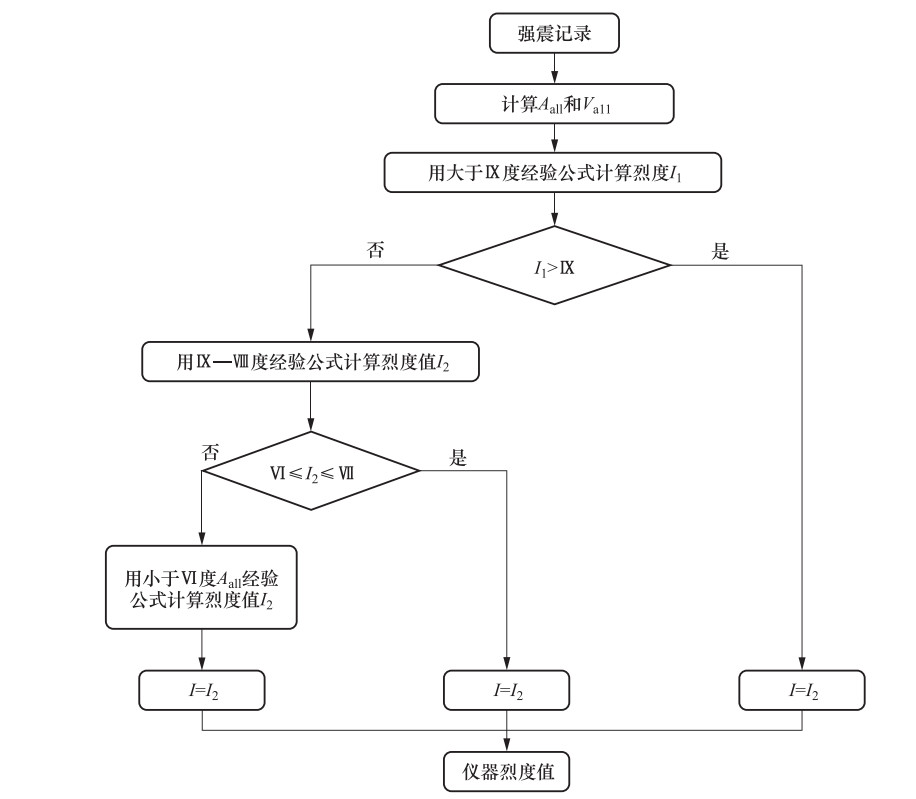
摘要: 通过分析研究美国地质调查局和日本气象厅的仪器烈度算法，认为计算仪器烈度要综合考虑幅值、频谱、持时等地震动参数的影响，创新地提出了利用三分向合成加速度、速度计算仪器烈度，并通过汶川8.0级地震进行验证。结果表明，本文推荐的仪器烈度算法，其结果具有较高的准确性和可靠性，可为地震烈度速报提供参考。Abstract: Strong motion observation is very important for the nuclear power plant, High-speed Rail and other important project. In this paper, the amplitude, frequency spectrum, duration of ground motion parameters are all considered, innovation land have put forward the new method of seismic intensity which is synthesized by three components, through the analysis of instrumental intensity method of the U.S. Geological Survey (USGS) and the Japan Meteorological Agency. This method is verified by the Wenchuan earthquake, which may provide useful references to seismic intensity rapid assessment.
-
Key words:
- Instrumental seismic intensity /
- Ground motion parameters /
- Aall
-
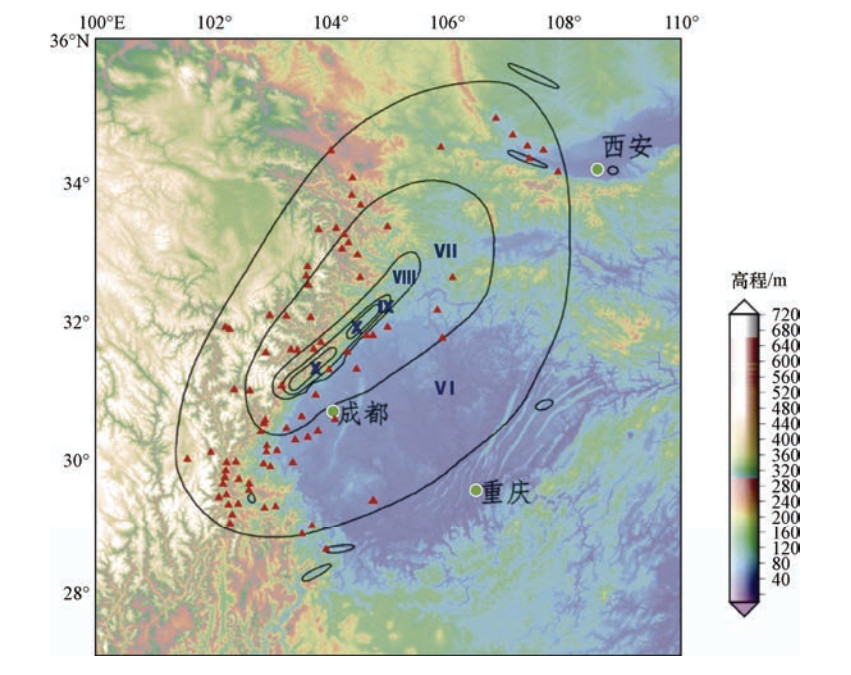
表 1 强震记录
Table 1. Strong motion records
地震名称 台站名称 烈度 宁洱地震 正兴 Ⅵ 德化 Ⅵ 勐先 Ⅵ 攀枝花地震 台站1 Ⅵ 台站2 Ⅵ 台站3 Ⅵ 台站4 Ⅵ 台站5 Ⅵ 台站6 Ⅶ 台站7 Ⅶ 台站8 Ⅷ 姚安地震 祥云禾甸乡 Ⅵ 盈江地震 梁河地震 Ⅵ 勐嘎河一级电站 Ⅵ 勐嘎村小学 Ⅶ 苏典乡政府 Ⅶ 新疆地震 台站1 Ⅵ 台站2 Ⅵ 
下载: 导出CSV
表 2 判定结果统计
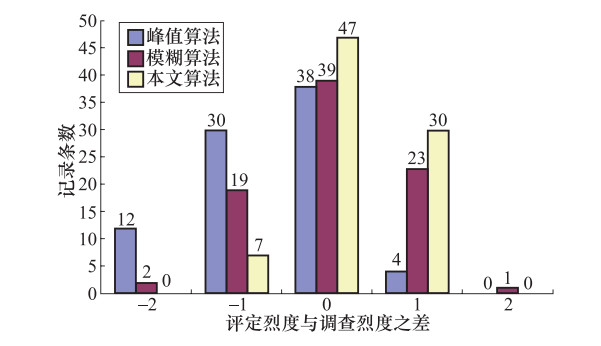
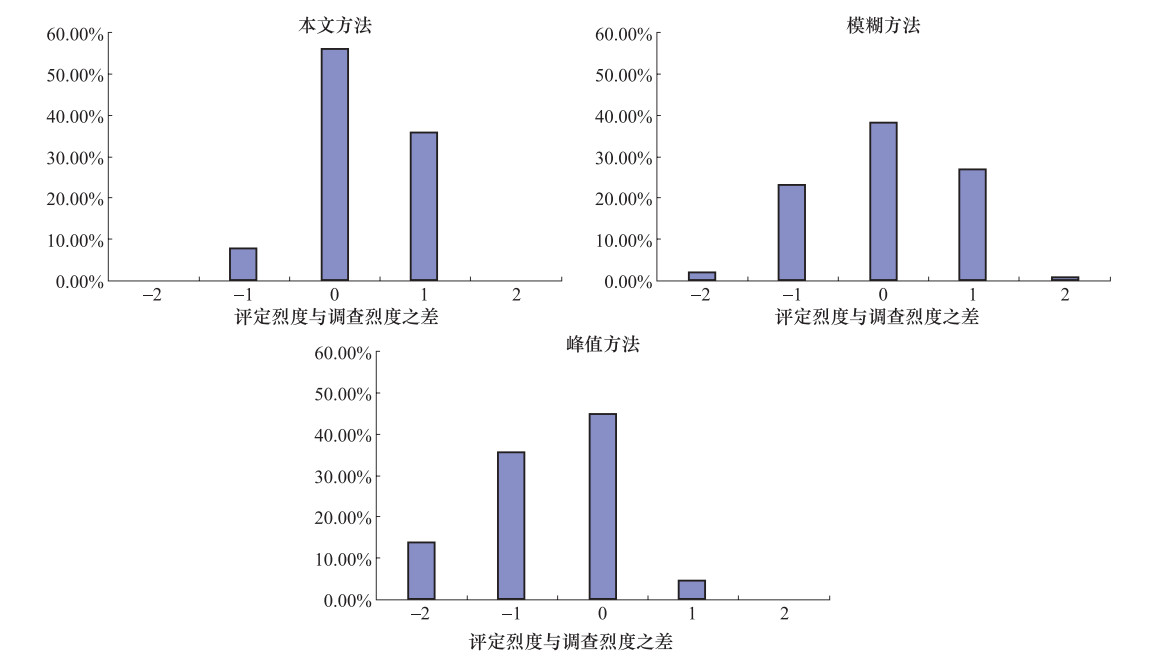
Table 2. Statistical analysis of the three methods
统计项 峰值评定 模糊算法 本文算法 相符率 45%（38台） 46%（39台） 56%（47台） 可接受率（±1度） 86%（72台） 96%（81台） 100%（84台）
下载: 导出CSV
-
陈志高, 黄俊, 2015.核电站地震监测系统及其开发进展.大地测量与地球动力学, 35(6):1065-1068, 1073. http://www.cnki.com.cn/Article/CJFDTOTAL-DKXB201506037.htm 冯德益, 林命周, 吴国有等, 1989.地震烈度的两种模糊评定方法.地震工程与工程振动, 9(2):45-56. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000005169661 何召壮, 2012.从日本福岛核泄漏事故看跨国核污染的国家责任.青岛: 中国海洋大学. http://cdmd.cnki.com.cn/Article/CDMD-10423-1012504255.htm 胡聿贤, 1988.地震工程学.北京:地震出版社. 金星, 张红才, 李军等, 2010.地震仪器烈度标准研究报告.福州:福建省地震局. 金星, 张红才, 李军等, 2013.地震仪器烈度标准初步研究.地球物理学进展, 28(5):2336-2351. http://d.old.wanfangdata.com.cn/Periodical/dqwlxjz201305016 李亮, 2011.基于地震动参数的烈度计算方法研究.哈尔滨:中国地震局工程力学研究所. 李敏, 2010.地震动加速度反应谱与地震烈度的关系研究.哈尔滨:中国地震局工程力学研究所. 李山有, 金星, 马强等, 2004.地震预警系统与智能应急控制系统研究.世界地震工程, 20(4):21-26. doi: 10.3969/j.issn.1007-6069.2004.04.003 刘锡荟, 王孟玫, 汪培庄, 1983.模糊烈度.地震工程与工程振动, 3(3):62-75. http://d.old.wanfangdata.com.cn/Periodical/sxdsjyrs201120010 苏经宇, 周锡元, 谭健, 1991.地震烈度的模糊预测模型.地震学报, 13(3):387-394. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000000376086 袁一凡, 1998.由地震动三要素确定地震动强度(烈度)的研究.哈尔滨:国家地震局工程力学研究所. 郑华, 魏淑虹, 2015.核电厂地震自动停堆综述.核科学与工程, 35(4):664-674. doi: 10.3969/j.issn.0258-0918.2015.04.013 周正华, 周雍年, 赵刚, 2002.强震近场加速度峰值比和反应谱统计分析.地震工程与工程振动, 22(3):15-18. doi: 10.3969/j.issn.1000-1301.2002.03.003 Brackman T. B., Withers M., 2006. Implementing ShakeMap for the New Madrid seismic zone. Seismological Research Letters, 77 (4):445-452. doi: 10.1785/gssrl.77.4.445 Kuwata Y., Takada S., 2002. Instantaneous instrumental seismic intensity and evacuation. Journal of Natural Disaster Science, 24 (1):35-42. Wald D. J., Quitoriano V., Heaton T. H., et al., 1999. TriNet "ShakeMaps":rapid generation of peak ground motion and intensity maps for earthquakes in Southern California. Earthquake Spectra, 15 (3):537-555. doi: 10.1193/1.1586057 -
点击查看大图
图(4) / 表(2)
计量
- 文章访问数: 4798
- HTML全文浏览量: 88
- PDF下载量: 85
- 被引次数: 0
