Stochastic Finite Fault Method and Its Engineering Applications
-
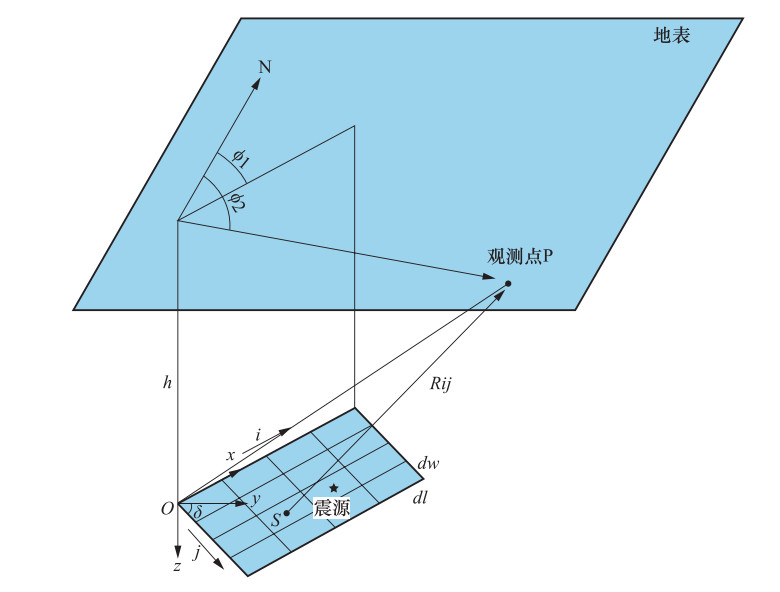
摘要: 随机有限断层法作为半经验半理论的地震动合成方法,综合考虑了震源、传播路径以及场地条件对地震动的影响,可在工程关注的频率范围内模拟地震动时程,为实现较大区域地震动模拟提供了一种有效的方法。本文系统阐述了随机有限断层法的基本原理、静力学拐角频率模型及动拐角频率模型的发展;分析了主要模型参数(断层尺度、破裂速度、剪切波速及应力降)、Kappa因子和介质品质因子的取值原则,并结合中国大陆的实际情况给出了相应的取值范围;最后讨论了现有模拟方法在考虑参数取值、子断层划分和子断层之间相互作用等方面的不足以及能量处理方式上的缺陷,明确了随机有限断层法发展的方向。Abstract: As a semi-empirical and semi-theoretical synthetic method of ground motion, stochastic finite fault method can comprehensively consider the impact of source, propagation path and site conditions, and can effectively simulate the seismic time history within the frequency range of engineering interest. It provides an effective means for the ground motion simulation in a large region. In this paper, the basic principle of stochastic finite fault method and the development of static corner frequency model and dynamic corner frequency model are firstly systematically expounded. Principles of the values of the major source parameters (fault size, rupture velocity, shear wave velocity, stress drop), kappa factor and Q value are analyzed. According to the actual situation in China, the corresponding range of values are provied. Finally, the shortcomings of present existing simulation methods in considering the parameter value, the interaction among sub-faults, energy treatment methods and fault division have been discussed. The development direction of stochastic finite fault method are somehow clarified.
-
Key words:
- Ground motion simulation /
- Stochastic finite fault method /
- Stress drop /
- Kappa factor /
- Quality factor
-
表 1 断层尺度与矩震级的统计关系
Table 1. Statistical relationship between the fault scale and moment magnitude
断层类型 断层长度/km 断层面积/km2 走滑断层 $ \lg L=-2.57+0.62{{M}_\text{W}} $ $ \lg S\text{=}-3.42+0.90{{M}_\text{W}} $ 正断层 $ \lg L\text{=}-1.88+0.50{{M}_\text{W}} $ $ \lg S\text{=}-2.87+0.82{{M}_\text{W}} $ 逆断层 $ \lg L\text{=}-2.42+0.58{{M}_\text{W}} $ $ \lg S\text{=}-3.99+0.98{{M}_\text{W}} $ 所有断层类型 $\lg L\text{=}-2.44+0.59{{M}_\text{W}} $ $ \lg S\text{=}-3.49+0.91{{M}_\text{W}} $ 表 2 中国大陆Q0值范围
Table 2. The range of Q0 value in Chinese mainland
区域 Q0 n 青藏高原褶皱区 200—250 0.5—0.7 松潘甘孜褶皱区 250—300 滨太平洋褶皱区 275—300 0.5—0.7 昆仑-秦岭褶皱区 275—325 塔里木地台 350—425 0.3—0.5 扬子块体 325—400 0.45—0.55 中朝块体 325—400 0.3—0.5 华南褶皱系(西高东低) 275—400 0.45—0.55 天山-兴安褶皱区 300—425 0.3—0.5 西伯利亚地台南端 450—500 0.45—0.7 注:青藏高原褶皱区包括冈底斯念-青唐古拉褶皱系、喀拉昆仑-唐古拉褶皱系和三江褶皱系;滨太平洋褶皱区包括东南沿海褶皱区、延边褶皱区和那丹哈达优地槽褶皱带;昆仑-秦岭褶皱区包括东昆仑褶皱系、秦岭褶皱系以及祁连褶皱系。 表 3 云南地区Q值公式
Table 3. The formula of calculating Q value in Yunnan Province
区域 Q 云南地区 $ Q\text{=}238{{f}^{0.338}} $ 云南东部地区 $Q\text{=}199.6{{f}^{0.434}} $ 云南西部地区 $ Q\text{=}281{{f}^{0.349}} $ 滇西地区 $ Q\text{=}102.6{{f}^{0.687}} $ 滇中地区 $ Q\text{=}92.7{{f}^{0.553}} $ -
常莹, 2011.基于断层破裂过程分解法模拟近断层宽频地震动.北京:中国地震局地球物理研究所. 陈晓非, 2009.浅源大地震超剪切破裂机理研究.见: 中国地球物理·2009.合肥: 中国地球物理学会. 丛连理, 胡家富, 傅竹武等, 2002.中国大陆及邻近地区Lg尾波的Q值分布.中国科学(D辑), 32(8):617-624. http://d.old.wanfangdata.com.cn/Periodical/zgkx-cd200208001 高阳, 潘华, 汪素云, 2014.中强地震随机有限断层模型应力降参数的确定方法.震灾防御技术, 9(4):733-747. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?flag=1&file_no=20140401&journal_id=zzfyjs 高阳, 2016.随机有限断层法模拟中强地震近场地震动的研究及应用.国际地震动态, (1):43-44. http://www.cnki.com.cn/Article/CJFDTOTAL-GJZT201601012.htm 郭明珠, 贾连军, 铁瑞等, 2011.剪切波速测试方法的现状分析.西北地震学报, 33(S1):21-23. http://d.old.wanfangdata.com.cn/Periodical/xbdzxb2011z1005 胡家富, 丛连理, 苏有锦等, 2003.云南及周边地区Lg尾波Q值的分布特征.地球物理学报, 46(6):809-813. doi: 10.3321/j.issn:0001-5733.2003.06.013 李英民, 赖明, 白绍良, 2002.从结构抗震设计理论看地震动输入.工程力学, (S1):549-554. http://d.old.wanfangdata.com.cn/Conference/4110927 笠原太一, 1984.地震力学.赵仲和, 译.北京: 地震出版社. 梁俊伟, 2015.基于能量的随机有限断层法研究.南昌: 南昌航空大学. http://www.cnki.com.cn/Article/CJFDTotal-NCHK201502002.htm 刘建华, 刘福田, 阎晓蔚等, 2004.华北地区Lg尾波衰减研究——Lg尾波Q0地震成像.地球物理学报, 47(6):1044-1052. doi: 10.3321/j.issn:0001-5733.2004.06.017 刘丽芳, 苏有锦, 刘杰等, 2010.云南和四川中小地震应力降时空特征研究.地震研究, 33(3):314-319. doi: 10.3969/j.issn.1000-0666.2010.03.012 卢育霞, 石玉成, 2003.1988年肃南地震近场地面运动的随机模拟.岩石力学与工程学报, 22(S2):2794-2799. http://d.old.wanfangdata.com.cn/Periodical/yslxygcxb2003z2054 马宏生, 刘杰, 张国民等, 2006.云南地区尾波Qc值的分布特征及其初步解释.地震, 26(3):37-43. http://d.old.wanfangdata.com.cn/Periodical/diz200603005 毛燕, 徐彦, 王彬等, 2005.四川及邻区Lg尾波的Q值分布特征.地震研究, 28(1):38-42. doi: 10.3969/j.issn.1000-0666.2005.01.008 秦嘉政, 阚荣举, 1986.用近震尾波估算昆明及其周围地区的Q值和地震矩.地球物理学报, 29(2):145-156. doi: 10.3321/j.issn:0001-5733.1986.02.005 秦建增, 刘昌铨, 嘉世旭等, 1997.唐山地震区地壳Q值结构的研究.见: 1997年中国地球物理学会第十三届学术年会论文集.上海: 中国地球物理学会. 师海阔, 朱新运, 贺永忠等, 2011.利用Sato模型对宁夏及邻区尾波Q值的研究.地震, 31(1):118-126. http://d.old.wanfangdata.com.cn/Periodical/diz201101013 石玉成, 陈厚群, 李敏等, 2005.随机有限断层法合成地震动的研究与应用.地震工程与工程振动, 25(4):18-23. doi: 10.3969/j.issn.1000-1301.2005.04.003 苏伟, 吴建平, 明跃红等, 2006.Lg尾波Q0值与中国大陆及邻区的地质构造关系.地震学报, 28(2):132-140. doi: 10.3321/j.issn:0253-3782.2006.02.003 苏有锦, 2009.云南地区地震波衰减(Q值)结构反演成像研究.合肥: 中国科学技术大学. http://cdmd.cnki.com.cn/article/cdmd-10358-2010042981.htm 孙吉泽, 俞言祥, 何金刚等, 2013.2013年乌鲁木齐MS5.6和MS5.1地震强地震动模拟研究.地震学报, 39(5):751-763. http://d.old.wanfangdata.com.cn/Periodical/dizhen201705010 孙晓丹, 陶夏新, 王国新等, 2009.地震动随机合成中与震源谱相关的动力学拐角频率.地震学报, 31(5):537-543. doi: 10.3321/j.issn:0253-3782.2009.05.006 孙晓丹, 2010.强地震动场估计中若干问题的研究.哈尔滨: 哈尔滨工业大学. http://cdmd.cnki.com.cn/article/cdmd-10213-2011012837.htm 陶夏新, 陈富, 孙晓丹, 2012.强地震动随机合成中震源谱模型的改进.岩土工程学报, 34(3):504-507. http://d.old.wanfangdata.com.cn/Thesis/D259854 王国新, 2001.强地震动衰减研究.哈尔滨:中国地震局工程力学研究所. 王国新, 史家平, 2008.近场强地震动合成方法研究及地震动模拟.东北地震研究, 24(2):4-10. doi: 10.3969/j.issn.1674-8565.2008.02.002 王海云, 2004.近场强地震动预测的有限断层震源模型.哈尔滨:中国地震局工程力学研究所. 王振宇, 2017.高频地震动随机模拟方法研究.哈尔滨:中国地震局工程力学研究所. 姚虹, 冯锐, 1988.中国东西剖面的地壳Q结构研究.地震研究, 11(6):539-550. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000000384145 袁一凡, 田启文, 2012.工程地震学.北京:地震出版社. 臧绍先, 1984.地震应力降与岩石破裂应力降.地震学报, 6(2):182-194. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000000375738 张翠然, 陈厚群, 李敏, 2011.采用随机有限断层法生成最大可信地震.水利学报, 42(6):721-728. http://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201106017.htm 张龙文, 2013.地震加速度时程合成方法研究.南昌: 南昌航空大学. http://cdmd.cnki.com.cn/Article/CDMD-10406-1014006798.htm 赵翠萍, 陈章立, 华卫等, 2011.中国大陆主要地震活动区中小地震震源参数研究.地球物理学报, 54(6):1478-1489. doi: 10.3969/j.issn.0001-5733.2011.06.007 郑天愉, 姚振兴, 1993.用近场记录研究唐山地震的震源过程.地球物理学报, 36(2):174-184. doi: 10.3321/j.issn:0001-5733.1993.02.006 钟菊芳, 2014.近场强地震动模拟现状分析.南昌航空大学学报:自然科学版, 28(2):1-8. http://d.old.wanfangdata.com.cn/Periodical/nchkgyxyxb201402001 朱百慧, 2016.强震数据Kappa值影响因素的讨论.哈尔滨:中国地震局工程力学研究所. Abe K., 1975. Reliable estimation of the seismic moment of large earthquakes. Journal of Physics of the Earth, 23(4):381-390. doi: 10.4294/jpe1952.23.381 Abercrombie R. E., 1995. Earthquake source scaling relationships from −1 to 5 ML using seismograms recorded at 2.5km depth. Journal of Geophysical Research, 100 (B12):24015-24036. doi: 10.1029/95JB02397 Aki K., Lee W. H. K., 1976. Determination of three-dimensional velocity anomalies under a seismic array using first P arrival times from local earthquakes:1. A homogeneous initial model. Journal of Geophysical Research, 81 (23):4381-4399. doi: 10.1029/JB081i023p04381 Aki K., Richards P. G., 1980. Quantitative seismology theory and methods. San Francisco:W.H. Freeman and Company. Allmann B. P., Shearer P. M., 2007. Spatial and temporal stress drop variations in small earthquakes near Parkfield, California. Journal of Geophysical Research, 112 (B4):B04305. doi: 10.1029-2006JB004395/ Anderson J. G., Hough S. E., 1984. A model for the shape of the Fourier amplitude spectrum of acceleration at high frequencies. Bulletin of the Seismological Society of America, 74 (5):1969-1993. http://www.researchgate.net/publication/215754549_A_model_for_the_shape_of_the_Fourier_amplitude_spectrum_at_high_frequencies Anderson J. G., 1991. A preliminary descriptive model for the distance dependence of the spectral decay parameter in southern California. Bulletin of the Seismological Society of America, 81 (6):2186-2193. Andrews D. J., 1976. Rupture propagation with finite stress in Antiplane Strain. Journal of Geophysical Research, 81 (20):3575-3582. doi: 10.1029/JB081i020p03575 Atkinson G. M., 1996. The high-frequency shape of the source spectrum for earthquakes in eastern and western Canada. Bulletin of the Seismological Society of America, 86 (1A):106-112. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=d6b37d6f73367ec43ed271cbb0813fa6 Atkinson G. M., 2004. Empirical attenuation of ground-motion spectral amplitudes in southeastern Canada and the northeastern United States. Bulletin of the Seismological Society of America, 94 (6):2419-2423. doi: 10.1785/0120040161 Atkinson G. M., Assatourians K., Boore D. M., et al., 2009. A guide to differences between stochastic point-source and stochastic finite-fault simulations. Bulletin of the Seismological Society of America, 99 (6):3192-3201. doi: 10.1785/0120090058 Atkinson G. M., Goda K., Assatourians K., 2011. Comparison of nonlinear structural responses for accelerograms simulated from the stochastic finite-fault approach versus the hybrid broadband approach. Bulletin of the Seismological Society of America, 101(6):2967-2980. doi: 10.1785/0120100308 Beresnev I. A., Atkinson G. M., 1997. Modeling finite-fault radiation from the ωn spectrum. Bulletin of the Seismological Society of America, 87 (1):67-84. Beresnev I. A., Atkinson G. M., 1998. FINSIM-a FORTRAN program for simulating stochastic acceleration time histories from finite faults. Seismological Research Letters, 69 (1):27-32. doi: 10.1785/gssrl.69.1.27 Beresnev I. A., Atkinson G. M., 1998. Stochastic finite-fault modeling of ground motions from the 1994 Northridge, California, earthquake. Ⅰ. Validation on rock sites. Bulletin of the Seismological Society of America, 88 (6):1392-1401. Beresnev I. A., Atkinson G. M., 1999. Generic finite-fault model for ground-motion prediction in eastern North America. Bulletin of the Seismological Society of America, 89 (3):608-625. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=455821ae43b43aa59ca91d713fc0ae43 Boore D. M., ,Joyner WB, 1997. Site amplifications for generic rock sites. Bulletin of the Seismological Society of America. 87 (2):327-341. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0210394413/ Boore D. M., 2009. Comparing stochastic point-source and finite-source ground-motion simulations:SMSIM and EXSIM. Bulletin of the Seismological Society of America, 99 (6):3202-3216. doi: 10.1785/0120090056 Bouchon M., Sekiguchi H., Irikura K., et al., 1998. Some characteristics of the stress field of the 1995 Hyogo-ken Nanbu (Kobe) earthquake. Journal of Geophysical Research, 103 (B10):24271-24282. doi: 10.1029/98JB02136 Brune. J.N., 1970. Tectonic stress and the spectra of seismic shear waves from earthquakes. Journal of Geophysical Research. 75 (26):4997-5009. doi: 10.1029/JB075i026p04997 Chandler A. M., Lam N. T. K., Tsang H. H., 2006. Near-surface attenuation modelling based on rock shear-wave velocity profile. Soil Dynamics and Earthquake Engineering, 26 (11):1004-1014. doi: 10.1016/j.soildyn.2006.02.010 Chen S. Z., Atkinson G. M., 2002. Global comparisons of earthquake source spectra. Bulletin of the Seismological Society of America, 92 (92):885-895. doi: 10.1785-0120010152/ Chopra S., Kumar D., Choudhury P., et al., 2012. Stochastic finite fault modelling of Mw4.8 earthquake in Kachchh, Gujarat, India. Journal of Seismology, 16 (3):435-449. doi: 10.1007/s10950-012-9280-0 Cotton F., Scherbaum F., Bommer J. J., et al., 2006. Criteria for selecting and adjusting ground-motion models for specific target regions:application to central Europe and rock sites. Journal of Seismology, 10 (2):137-156. doi: 10.1007/s10950-005-9006-7 Edwards B., Fäh D., Giardini D., 2011. Attenuation of seismic shear wave energy in Switzerland. Geophysical Journal International, 185 (2):967-984. doi: 10.1111/gji.2011.185.issue-2 Fukuyama E., Olsen K. B., 2002. A condition for super-shear rupture propagation in a heterogeneous stress field. Pure and Applied Geophysics, 159 (9):2047-2056. doi: 10.1007/s00024-002-8722-y Guatteri M., Mai P. M., Beroza G. C., et al., 2003. Strong ground-motion prediction from stochastic-dynamic source models. Bulletin of the Seismological Society of America, 93 (1):301-313. doi: 10.1785/0120020006 Hanks T. C., McGuire R. K., 1981. The character of high-frequency strong ground motion. Bulletin of the Seismological Society of America, 71 (6):2071-2095. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=df58c2f1273e0436e69f9d0b2bab856c Hardebeck J. L., Hauksson E., 1997. Static stress drop in the 1994 Northridge, California, aftershock sequence. Bulletin of the Seismological Society of America, 87 (6):1495-1501. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=8e5d0c04733ff45ba677296a892a1f08 Hardebeck J. L., Aron A., 2009. Earthquake stress drops and inferred fault strength on the Hayward fault, East San Francisco Bay, California. Bulletin of the Seismological Society of America, 99 (3):1801-1814. doi: 10.1785/0120080242 Harris R. A., Day S. M., 1999. Dynamic 3D simulations of earthquakes on En Echelon Faults. Geophysical Research Letters, 26 (14):2089-2092. doi: 10.1029/1999GL900377 Hartzell S. H., Heaton T. H., 1983. Inversion of strong ground motion and teleseismic waveform data for the fault rupture history of the 1979 Imperial Valley, California, earthquake. Bulletin of the Seismological Society of America, 73 (6A):1553-1583. https://www.researchgate.net/publication/251592818_Inversion_of_strong_ground_motion_and_teleseismic_waveform_data_for_the_fault_rupture_history_of_the_1979_Imperial_Valley_California_earthquake Heaton T. H., 1990. Evidence for and implications of self-healing pulses of slip in earthquake rupture. Physics of the Earth and Planetary Interiors, 64 (1):1-20. doi: 10.1016/0031-9201(90)90002-F Housner G. W., 1947. Characteristics of strong-motion earthquakes. Bulletin of the Seismological Society of America, 37 (l):19-31. http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_1418725f443cdbac5adcbbbb6187f02a Jin A. S., Aki K., 1988. Spatial and temporal correlation between coda Q and seismicity in China. Bulletin of the Seismological Society of America, 78 (2):741-769. https://www.researchgate.net/publication/290791515_Spatial_and_temporal_correlation_between_coda_Q_and_seismicity_in_China Jin A. S., Moya C. A., Ando M., 2000. Simultaneous determination of site responses and source parameters of small earthquakes along the atotsugawa fault zone, Central Japan. Bulletin of the Seismological Society of America, 90 (6):1430-1445. doi: 10.1785/0119990140 Kamae K, Irikura K, Pikarta A, 1998. A Technique for Simulating Strong Ground Motion Using Hybrid Green's Function. Bulletin of the Seismological Society of America, 88 (2):357-367. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=eaad532fbb0c1cf44b3111ddae5dc308 Kanamori H., Anderson D. L., 1975. Theoretical basis of some empirical relations in seismology. Bulletin of the Seismological Society of America, 65 (5):1073-1095. http://www.researchgate.net/publication/228077798_Theoretical_basis_of_some_empirical_relations_in_seismology Kanamori H., Rivera L., 2004. Static and dynamic scaling relations for earthquakes and their implications for rupture speed and stress drop. Bulletin of the Seismological Society of America, 94 (1):314-319. doi: 10.1785/0120030159 Kilb D., Biasi G., Anderson J., et al., 2012. A Comparison of Spectral Parameter Kappa from Small and Moderate Earthquakes Using Southern California ANZA Seismic Network Data. Bulletin of the Seismological Society of America, 102 (1):284-300. doi: 10.1785/0120100309 Mayeda K., Walter W. R., 1996. Moment, energy, stress drop, and source spectra of western United States earthquakes from regional coda envelopes. Journal of Geophysical Research, 101 (B5):11195-11208. doi: 10.1029/96JB00112 McGuire, R.K., Hanks, T.C., 1980. RMS accelerations and spectral amplitudes of strong gound motion during the San Femando, Califomia earthquake. Bull. Seism Soc. Amer, 70:1907-1919. Miyake H., Iwata T., Irikura K., 2003. Source characterization for broadband ground-motion simulation:kinematic heterogeneous source model and strong motion generation area. Bulletin of the Seismological Society of America, 93 (6):2531-2545. doi: 10.1785/0120020183 Motazedian D., Atkinson G. M., 2005. Stochastic finite-fault modeling based on a dynamic corner frequency. Bulletin of the Seismological Society of America, 95 (3):995-1010. doi: 10.1785/0120030207 Nuttli, O. W., 1988. Lg magnitudes and yield estimates for underground Novaya Zemlya nuclear explosions. Bulletin of the Seismological Society of America, 78 (2): 873-884. Papageorgiou A. S., Aki K., 1983. A specific barrier model for the quantitative description of inhomogeneous faulting and the prediction of strong ground motion. Part Ⅱ. Applications of the model. Bulletin of the Seismological Society of America, 73 (4):953-978. https://www.sciencedirect.com/science/article/pii/0148906284904984 Sato R., 1999. Theoretical basis on relationships between focal parameters and earthquake magnitude. Journal of Physics of the Earth, 27 (5):353-372. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=J-STAGE_3391661 Scholz C. H., 2002. The mechanics of earthquakes and faulting. 2nd ed. Cambridge:Cambridge University Press. Shi J. H., Kim W. Y., Richards P. G., 1998. The corner frequencies and stress drops of intraplate earthquakes in the northeastern United States. Bulletin of the Seismological Society of America, 88 (2):531-542. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=7dde414834ae2d5316d89f6d2346edaa Shih X. R., Chun K. Y., Zhu T., 1994. Attenuation of 1-6s Lg waves in Eurasia. Journal of Geophysical Research, 99 (B12):23859-23874. doi: 10.1029/94JB02163 Somerville P., Irikura K., Graves R., et al., 1999. Characterizing crustal earthquake slip models for the prediction of strong ground motion. Seismological Research Letters, 70 (1):59-80. doi: 10.1785/gssrl.70.1.59 Sun X. D., Tao X. X., Chen F., 2010. Improvements of corner frequency and scaling factor for stochastic finite-fault modeling. Earthquake Engineering and Engineering Vibration, 9 (4):503-511. doi: 10.1007/s11803-010-0032-2 Sun X. D., Tao X. X., Duan S. S., et al., 2013. Kappa (k) derived from accelerograms recorded in the 2008 Wenchuan mainshock, Sichuan, China. Journal of Asian Earth Sciences, 73:306-316. doi: 10.1016/j.jseaes.2013.05.008 Sun Xiaodan, Tao Xiaxin, Wang Guoxin, Liu Taojun, 2009. Dynamic corner frequency in source spectral model for stochastic synthesis of ground motion. Earthquake Science, 22 (3):271-276. doi: 10.1007/s11589-009-0271-3 Tao X.X., Sun X.D., Wang G.X, 2008. An dynamic corner frequency based source spectral model. Proc. of the 14 World Conference on Earthquake Engineering. Tsai C. C. P., Chen K. C., 2000. A model for the high-cut process of strong-motion accelerations in terms of distance, magnitude, and site condition:an example from the SMART 1 Array, Lotung, Taiwan. Bulletin of the Seismological Society of America, 90 (6):1535-1542. doi: 10.1785/0120000010 Tusa G., Gresta S., 2008. Frequency-dependent attenuation of P waves and estimation of earthquake source parameters in southeastern Sicily, Italy. Bulletin of the Seismological Society of America, 98 (6):2772-2794. doi: 10.1785/0120080105 Van Houtte C., Drouet S., Cotton F., 2011. Analysis of the origins of k (Kappa) to compute hard rock to rock adjustment factors for GMPEs. Bulletin of the Seismological Society of America, 101 (6):2926-2941. doi: 10.1785/0120100345 Wang G. Q., 2001. Comparisons of ground motions from five aftershocks of the 1999 Chi-Chi, Taiwan, earthquake with empirical predictions largely based on data from California. Bulletin of the Seismological Society of America, 91 (5):1212-1217. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=5d7512a3024e09f35edfb0fa0a109ceb Wells D. L., Coppersmith K. J., 1994. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bulletin of the Seismological Society of America, 84 (4):974-1002. http://www.researchgate.net/publication/215755871_New_empirical_relationships_among_magnitude_rupture_length_rupture_width_rupture_area_and_surface_displacement Zhao D. P., Hasegawa A., Horiuchi S., 1992. Tomographic imaging of P and S wave velocity structure beneath northeastern Japan. Journal of Geophysical Research, 97 (B13):19909-19928. doi: 10.1029/92JB00603 -



 下载:
下载:

