The Simulated Ground Motion of Chengdu Fault in Broadband Frequency by the Hybrid Method
-
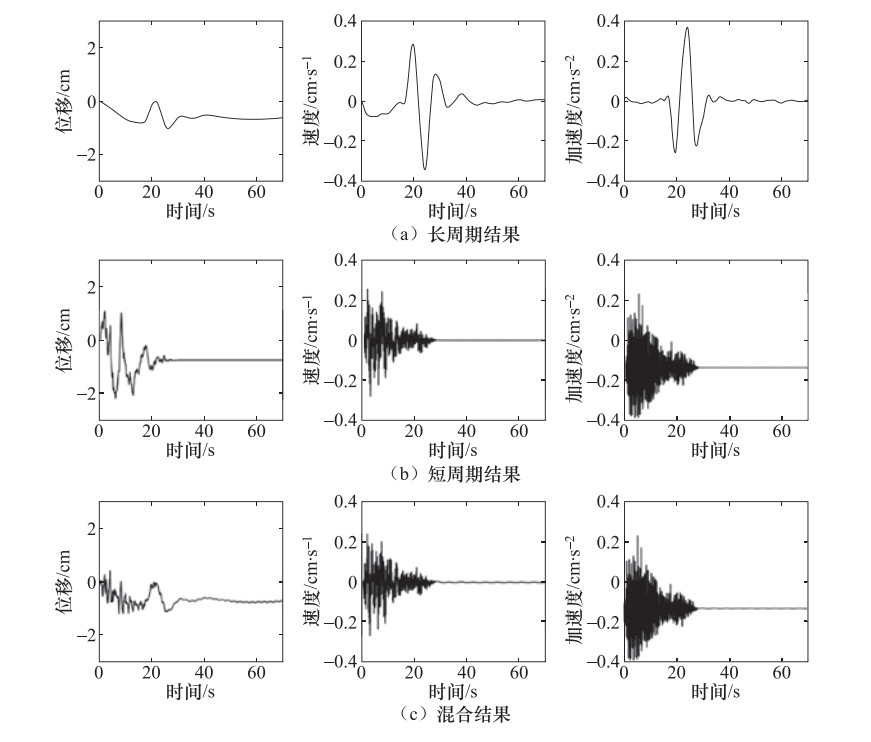
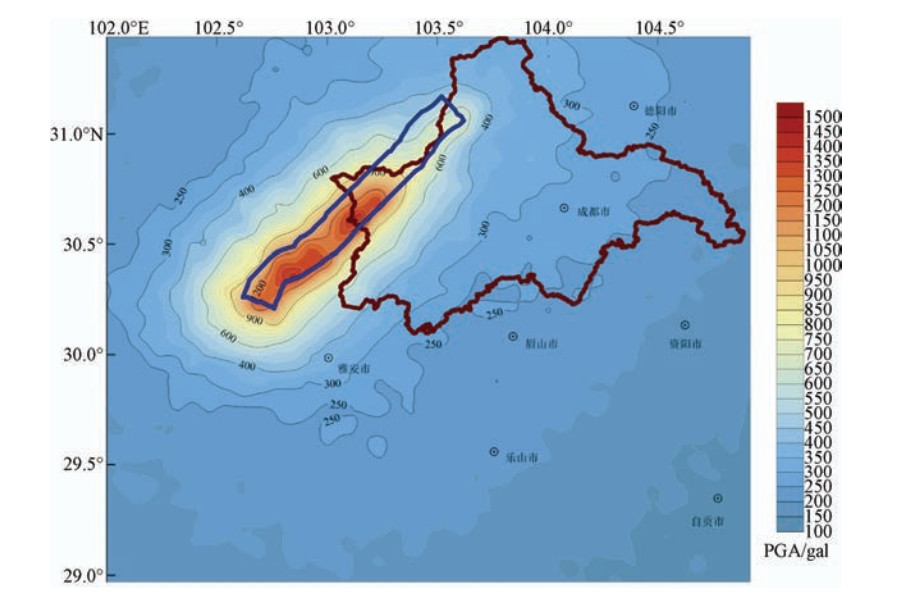
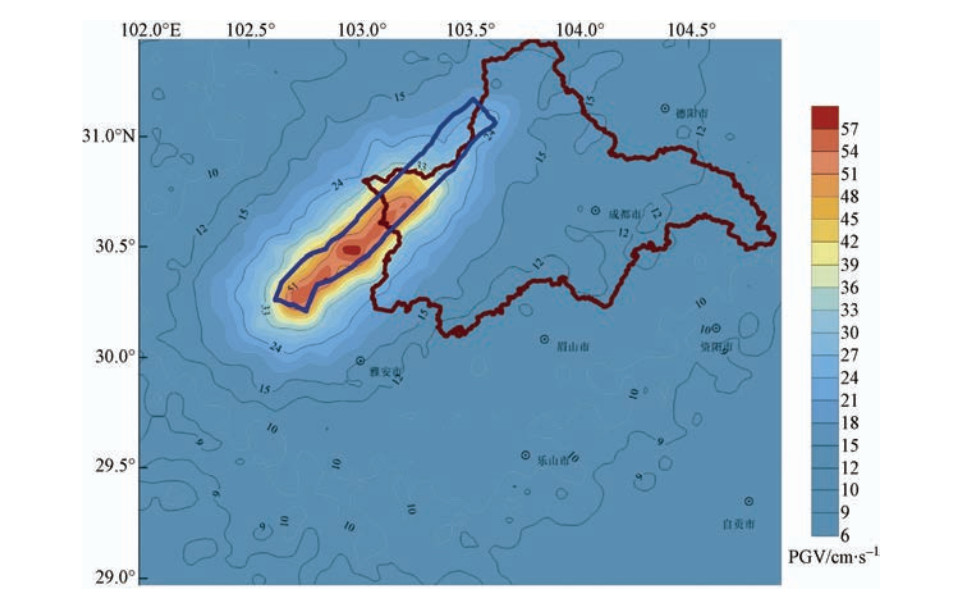
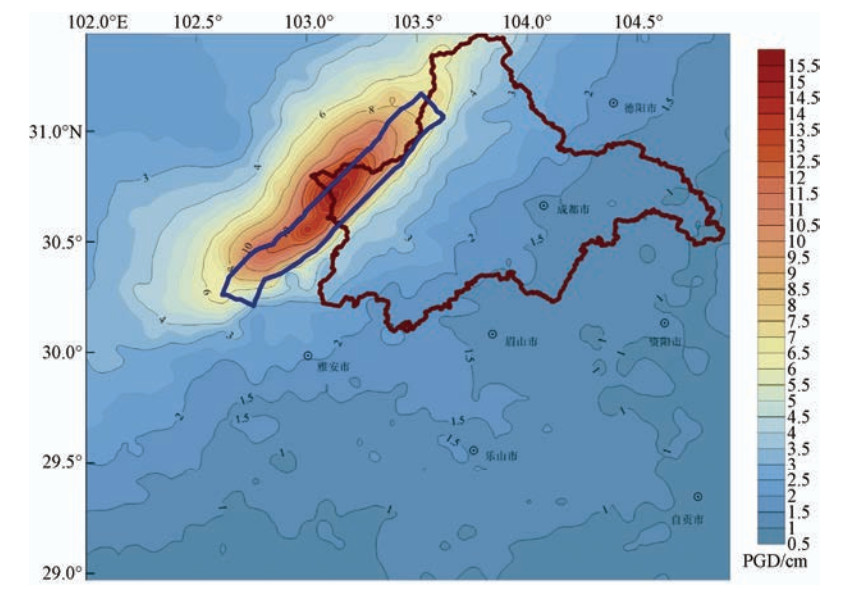
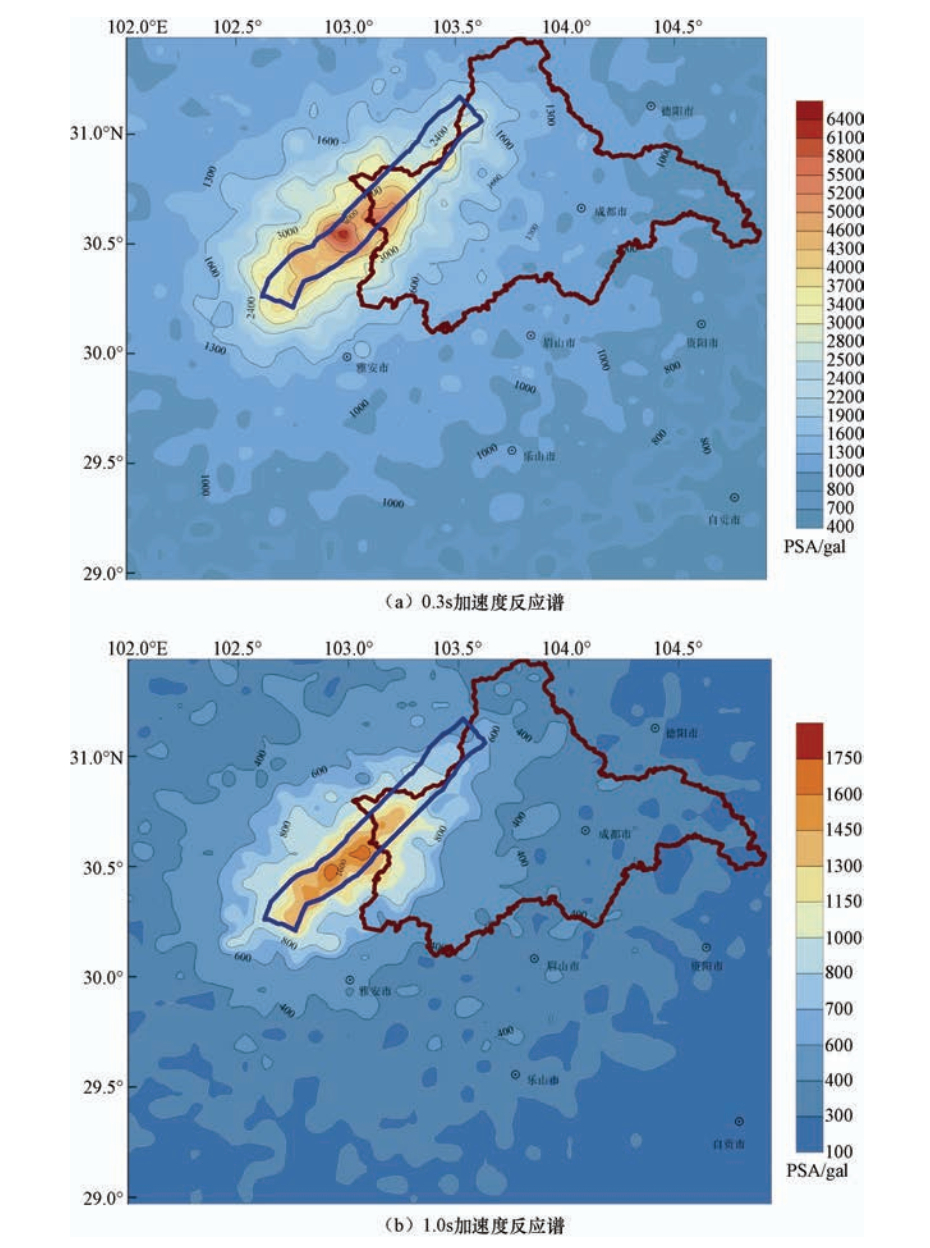
摘要: 首先，依据成都活断层探测的深、浅层地震勘探资料、钻井资料、地形资料，建立成都地区地下三维介质模型，并基于活断层确定的双石-大川断裂发生7.6级潜在地震的地震活动性探测结果，设定断层破裂震源模型，采用随机有限断层方法模拟短周期地震动、谱元法模拟长周期地震动，利用混合法通过频域合成技术获得了研究区域的宽频地震动。最后，讨论了合成结果的PGA、PGV、PGD以及0.3s和1.0s反应谱的分布特征，依据分布结果对成都市区进行了本次设定地震的地震动讨论。Abstract: Based on the seismic prospecting data of deep and shallow layers, drilling data and topographic data in Chengdu, a deep three-dimensional medium model of Chengdu is established. Then, based on the data of Shuangshi-Dachuan fault survey the rupture source model of MS 7.6 potential earthquake is set up. The stochastic finite fault method is used to simulate the short period ground motion and the spectral element method is used to simulate the long period ground motion. The broadband seismic motion is obtained by the frequency domain synthesis technology of two parts. Finally, the distribution characteristics of the synthetic PGA, PGV, PGD, 0.3s response spectrum and 1.0s response spectrum are given and discussed.
-
引言
2020年5月18日21时47分，云南省巧家县小河镇（27.18°N，103.16°E）发生MS5.0地震，震源深度8 km。本次地震造成4人死亡，28人受伤，为2020年人员伤亡最严重的地震。地震发生在2014年鲁甸6.5级地震恢复重建区内，该区地质条件复杂，震时极易引发地质灾害。鲁甸6.5级地震曾引发大量滑坡、崩塌、滚石等地质灾害，造成多人伤亡（冀昆等，2014；帅向华等，2014；张彦琪等，2015，2016）。2006年盐津5.1级地震诱发严重的崩塌、滚石灾害，成为造成该次地震人员伤亡的首要原因（非明伦等，2006；白仙富等，2013；向小龙等，2015）。2012年彝良5.6、5.7级地震诱发大量崩塌、滚石、滑坡灾害，造成大量人员伤亡和房屋损坏，阻碍了救援道路，严重影响了救援进度（王东坡等，2013；翟敏刚等，2013；周桂华等，2013；白仙富等，2014）。
本文在概述云南省巧家县小河镇MS5.0级地震震区地质条件的基础上，详细阐述了此次地震人员伤亡、房屋震害及地质灾害特征，结合震区及周边震级相近的历史震例，对震区易发生小震致灾的成因进行分析，并提出减灾对策，以期为该地区未来防灾减灾工作提供参考。
1. 震区地质背景
巧家县位于云南省东北部昭通市西南区，西部、北部以金沙江为界，东北部以牛栏江为界，区域水系发育。在金沙江河谷深切割和药山山峰影响下，形成了亚高山深切割地貌。区内地层以易风化的中生界碎屑岩、砂岩、砾岩和古生界碳酸盐岩为主，元古界、新生界地层分布较少。岩浆岩大面积分布，主要为二叠纪峨眉山玄武岩。巧家县地处小江断裂、莲峰山断裂、则木河断裂的交汇区，新生代以来构造活动强烈，地震频发，弱震密集。
此外，受地形地貌、水文地质、地层岩性、地质构造、人类工程活动等影响，区内地质灾害种类多（滑坡、崩塌、泥石流、地面塌陷等），主要以中小型滑坡为主，总体上主要集中在沿金沙江右岸及其一、二级支流的河谷两侧，牛栏江河谷左岸及其次级支流沟谷和荞麦地河两岸（李瑞等，2015；李瑞，2016；杨德旭，2019）。
2. 灾情概况
2.1 人员伤亡
此次地震造成4人死亡，28人受伤。其中，死亡人员中2人为建筑物倒塌致死（图1），2人为滚石砸中致死。
图 1 垭口村良子小组生产用房倒塌Figure 1. The collapse of the production house of Liangzi group in Yakou village2.2 房屋震害
本次地震灾区房屋建筑结构类型主要有土木、砖混和框架结构，其中民居主要为鲁甸地震恢复重建及脱贫攻坚、农村危房改造工程改建的砖混结构房屋，普遍采取了抗震对策；学校、医院等公共场所建筑主要采用框架结构，部分为土木结构房屋（张原硕等，2020）。
现场调查情况显示，砖混结构民居在地震中多表现良好，为轻微破坏或基本完好，主要震害现象为墙体细小开裂、灰皮脱落等。个别民居由于地基处理方法不正确，造成地面开裂或墙体开裂。框架结构房屋基本完好。土木结构房屋多为保留的生产用房，为老旧“墙抬梁”式土木结构房屋，主要破坏现象为墙体开裂、梭掉瓦，少数房屋局部倒塌，个别房屋整体倒塌，是本次地震造成人员伤亡的主要原因。
2.3 地震地质灾害
本次地震虽未发生较大规模滑坡现象，但震中附近滚石、崩塌较常见，不仅造成了人员伤亡，对交通道路也产生了一定阻碍（图2）。本次地震因次生地质灾害造成2人遇难，均发生在地质灾害较集中的牛栏江两岸。
图 2 普谷村至垭口村段滚石造成交通中断Figure 2. Traffic interruption caused by rolling rocks from Pugu village to Yakou village2.4 烈度评估结果
云南省地震局根据现场调查点震害情况，结合震区构造背景、地震仪器烈度、余震序列分布等资料，确定了巧家MS5.0地震烈度图（图3）。本次地震灾区最高烈度为VI度，总面积约330 km2，涉及巧家县小河镇、新店镇、红山乡、东坪镇、药山镇和鲁甸县乐红镇（云南省地震局地震现场工作队，2020），直接经济损失约10 430万元。
图 3 云南省巧家县小河镇MS5.0地震烈度图Figure 3. Intensity distribution map of Qiaojia MS5.0 earthquake in Yunnan province注：地震烈度VI度，土木房屋个别倒塌，少数破坏；砖混房屋和框架房屋个别轻微破坏，多数基本完好。3. 震害特征与成因分析
3.1 震害特征
巧家县与其周边的鲁甸县、彝良县、盐津县和永善县为地震高发区。为分析地震灾区震害特征，选取巧家县及周边县城近年来发生的震级相近的地震进行对比分析，如表1、图4所示。
表 1 巧家县及周边县城震级相近的历史地震比较Table 1. Comparison of historical earthquakes of similar magnitude in Qiaojia county and surrounding areas震例 死亡人数/人 受伤人数/人 地震灾害致死人数/人 2020年巧家5.0级地震 4 28 2 2003年鲁甸5.0级地震 0 24 — 2003年鲁甸5.1级地震 4 94 — 2004年鲁甸5.6级地震 4 597 — 2006年盐津5.1、4.7级地震 2 67 20 2006年盐津5.1级地震 23（含失踪1人） 114 2010年巧家4.8级地震 0 17 — 2012年彝良5.7级和5.6级地震 81 834 65 2014年鲁甸6.5级地震 729（含失踪112人） 3 143 250 2014年永善5.0级地震 0 20 — 2014年永善5.3级地震 0 5 — 
图 4 巧家县及周边县城震级相近的历史地震分布Figure 4. Distribution map of historical earthquakes of similar magnitude in Qiaojia county and surrounding areas由表1可知，巧家县及周边县城不仅是地震高发区，且多次出现小震致灾的情况，特别是震后地质灾害屡屡造成人员死亡，如2006年7月22日和8月25日，盐津先后发生5.1级地震，因大量滚石和个别滑坡造成20人死亡，占总死亡人数的80%；2012年9月7日彝良发生5.7级地震，因滚石滑坡造成65人死亡，占总死亡人数的80%；2014年8月3日鲁甸发生6.5级地震，因滑坡等次生地质灾害造成250人死亡，占总死亡人数的34%。
3.2 成因分析
云南东北部昭通地区屡屡发生5.0级左右地震造成人员伤亡的主要原因为：
（1）建筑物抗震能力较差
昭通市下属的各县区农村地区建筑物抗震能力较差，根据近几年中国地震局组织的预评估实地调查资料，2015年前，鲁甸、彝良、巧家等地农村建筑中存在大量的“墙抬梁”式土木结构房屋，此种结构房屋抗震性能差。2014年鲁甸6.5级地震发生后，当地开展了恢复重建工作，但未覆盖整个区域，仍存在一定数量的抗震能力较差的土木和砖木结构房屋，这些房屋虽仅作为生产用房和家庭辅助用房，但在一定程度上存在风险。本次地震因老旧生产用房倒塌造成2人遇难。
（2）次生地质灾害严重
震区属于亚高山深切割地貌，区内水系发育、基岩易风化、构造活动强烈、人为干扰较大等因素导致基岩疏松，易发生地质灾害。不仅在震时，平时也常发生因降雨导致的大量地质灾害。地震发生后，出现严重地质灾害的阈值烈度较其他区域低，一般VI度时可能发生滚石和小型滑坡，VII度时可能出现大量落石和较严重的地质灾害，VIII度时可能出现大型滑坡和因地质灾害导致的道路中断。
（3）人口密集，且居住地多位于山坡及山底
该震区历史上为中原移民进入云南的通道，很多人迁居至此，人口密度较高。由于当地平地较少，大量人口集中居住在山坡及山底。从人口居住地地形坡度看，震区农村民居处于危险区域。强烈地震（6.5级以上）发生后，常出现滑坡体连带其中的建筑物共同滑落的现象，可能导致严重人员伤亡。
4. 减灾对策
此次地震灾害具有一定代表性，因此结合震区地质地貌特征、地层岩性特征、水文特征等客观条件，针对易出现的小震致灾情况，提出以下减灾对策：
（1）提高建筑物抗震能力
地震灾害造成重大损失的根本原因是灾区建筑物抗震能力不足以抵御灾区可能出现的地震冲击，巧家县抗震设防烈度为VII度，除县城和部分乡镇能够基本达到设防要求外，大部分农村地区建筑物抗震能力不满足设防要求，目前仍存在大量“墙抬梁”式土木结构房屋。因此，需进一步提高当地建筑物抗震能力，尤其是部分土木结构附属用房应尽快拆除或改造。
（2）合理规划，迁移高风险区居民点
云南东北部地区（包括鲁甸、彝良、巧家等）地质灾害危险性极高，震后易造成人员因滑坡滚石致死，主要因为当地农村民居距山体太近，很多民居甚至坐落在基岩不稳定的半山坡上。因此，需通过合理规划，对处于极危险地带的部分高危民居采取迁移对策，这是减轻震区地震灾害损失的关键对策之一。
（3）加强对震区的实地调查，提升防灾能力
应进一步加强对地震重点区域的现场调查与风险摸排，仅通过基础数据的收集与研究，难以发现真正的风险点、评估风险程度，很多因素和环节须通过现场实地调研、摸排才能发现并进行科学评估。巧家县及周边地区是地震灾害高发、易发区域，可称之为“地震灾害扶贫攻坚”的重点区域。在我国当前建筑物抗震设防能力普遍得到不同程度提高的情况下，此类区域是需高度关注的防灾减灾救灾重点区域。
（4）加强人员致死与烈度衰减关系的研究
目前缺少针对震后地质灾害可能导致人员伤亡的评估技术，也缺少相关的基础研究。而在我国西南区域震后地质灾害是导致人员死亡的主要原因之一，在某些地区甚至超过建筑物破坏导致的人员伤亡。因此，需提高震后科学评估水平，强化对各项救援救灾行动的支撑作用，开展震后地质灾害危害性和致死性的基础研究。
（5）加强对震源深度精确预测的研究
震源深度对极震区烈度的影响较大，但目前难以在震后得到准确的震源深度数据，正式速报中给出的震源深度数值常常会发生多次变化，因此如何在震后10 min左右给出较准确的震源深度需进一步研究。以往的烈度衰减关系中未考虑震源深度，导致对同一震级地震，无论震源深度是多少，极震区评估计算烈度均相同。因此，需研究新的烈度衰减关系，将震源深度纳入其中，提高快速评估的准确性。
-
图 5 计算区域加速度峰值（PGA）分布
Figure 5. The distribution of the peak ground acceleration (PGA) in the computation zone
图 6 计算区域速度峰值（PGV）分布
Figure 6. The distribution of the peak ground velocity (PGV) in the computation zone
图 7 计算区域位移峰值（PGD）分布
Figure 7. The distribution of the peak ground displacement (PGD) in the computation zone
图 8 计算区加速度反应谱（PSA）分布
Figure 8. The distribution of pseudo-spectral acceleration (PSA) in the computation zone
表 1 双石-大川断裂各段参数
Table 1. The fault parameters of Shuangshi-Dachuan fault
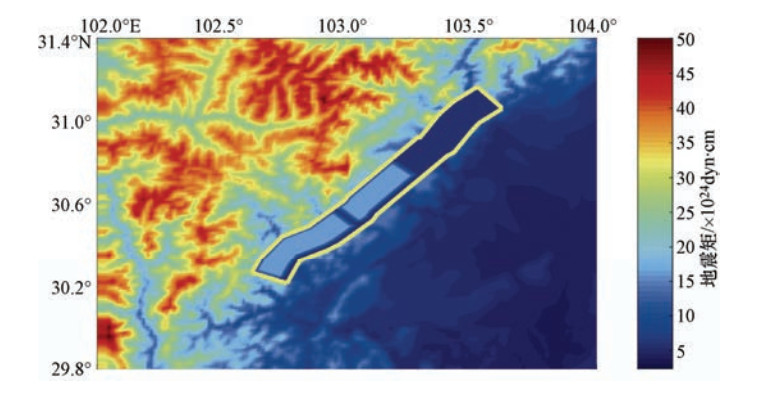
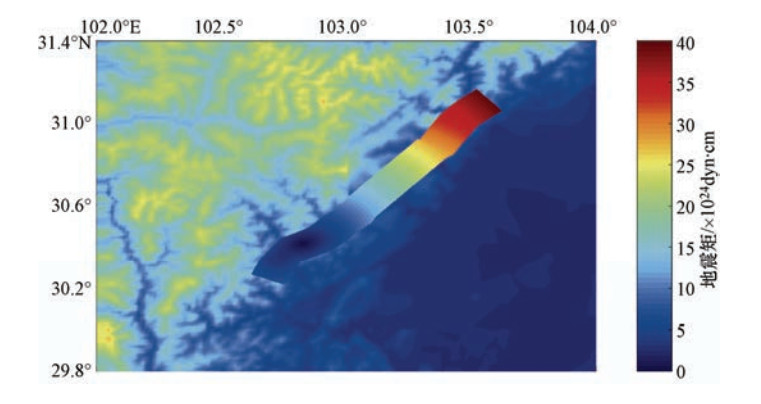
段号 端点纬度/°N 端点经度/°E 走向/° 倾向/° 长度/km 1 31.07 103.62 230 43.85 15 2 30.98 103.53 210 43.74 18 3 30.89 103.47 220 43.59 18 4 30.58 103.16 219 44.49 21 5 30.39 102.98 245 44.49 15 6 30.33 102.85 208 43.27 12 
下载: 导出CSV
表 2 双石-大川断裂计算参数
Table 2. The computation parameters of Shuangshi-Dachuan fault
参数 设定值 断层长度/km 126 断层宽度/km 24 滑动角/° 90 长度方向分割量（NL） 42 宽度方向分割量（NW） 8 子源的长度/km 3 子源的宽度/km 3 震级 7.6 总面积/km2 3024 最大凹凸体面积/km2 483 次级凹凸体面积/km2 181 破裂速度/km·s－1 2.9 破裂形式 同心圆 震源时间/s 3.01 品子因子Q(f) 500f0.5 应力降/bar 90
下载: 导出CSV
-
Atkinson G. M., Assatourians K., Boore D. M., et al., 2009. A guide to differences between stochastic point-source and stochastic finite-fault simulations. Bulletin of the Seismological Society of America, 99 (6):3192-3201. doi: 10.1785/0120090058 Atkinson G. M., Goda K., Assatourians K., 2011. Comparison of nonlinear structural responses for accelerograms simulated from the stochastic finite-fault approach versus the hybrid broadband approach. Bulletin of the Seismological Society of America, 101 (6):2967-2980. doi: 10.1785/0120100308 Boore D. M., 1983. Stochastic simulation of high-frequency ground motions based on seismological models of the radiated spectra. Bulletin of the Seismological Society of America, 73 (6):1865-1894. Boore D. M., 2003. Simulation of ground motion using the stochastic method. Pure and Applied Geophysics, 160 (4):635-676. http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_773ad1cbf1dcba3266bb060c1201c3cd Boore D. M., Thompson E. M., 2015. Revisions to some parameters used in stochastic-method simulations of ground motion. Bulletin of the Seismological Society of America, 105 (2A):1029-1041. doi: 10.1785/0120140281 Faccioli E., Maggio F., Paolucci R., et al., 1997. 2D and 3D elastic wave propagation by a pseudo-spectral domain decomposition method. Journal of Seismology, 1 (2):237-251. doi: 10.1023-A-1009758820546/ Frankel A., 2009. A constant stress-drop model for producing broadband synthetic seismograms:comparison with the Next Generation Attenuation relations. Bulletin of the Seismological Society of America, 99 (2A):664-680. doi: 10.1785/0120080079 Graves R. W., Pitarka A., 2004. Broadband time history simulation using a hybrid approach. In: Proceedings of the 13th World Conference Earthquake Engineering. Vancouver, Canada, 1-6 August. Graves R. W., Pitarka A., 2010. Broadband ground-motion simulation using a hybrid approach. Bulletin of the Seismological Society of America, 100 (5A):2095-2123. doi: 10.1785/0120100057 Komatitsch D., Vilotte J. P., 1998. The spectral element method:an efficient tool to simulate the seismic response of 2D and 3D geological structures. Bulletin of the Seismological Society of America, 88 (2):368-392. http://gji.oxfordjournals.org/cgi/ijlink?linkType=ABST&journalCode=ssabull&resid=88/2/368 Komatitsch D., Tromp J., 1999. Introduction to the spectral element method for three-dimensional seismic wave propagation. Geophysical Journal International, 139 (3):806-822. doi: 10.1046/j.1365-246x.1999.00967.x Motazedian D., Atkinson G. M., 2005. Stochastic finite-fault modeling based on a dynamic corner frequency. Bulletin of the Seismological Society of America, 95 (3):995-1010. doi: 10.1785/0120030207 Motazedian D., Moinfar A., 2006. Hybrid stochastic finite fault modeling of 2003, M 6.5, Bam earthquake (Iran). Journal of Seismology, 10 (1):91-103. doi: 10.1007/s10950-005-9003-x Pacor F., Cultrera G., Mendez A., et al., 2005. Finite fault modeling of strong ground motions using a hybrid deterministic-stochastic approach. Bulletin of the Seismological Society of America, 95 (1):225-240. doi: 10.1785/0120030163 Patera A. T., 1984. A spectral element method for fluid dynamics:laminar flow in a channel expansion. Journal of Computational Physics, 54 (3):468-488. doi: 10.1016/0021-9991(84)90128-1 Priolo E., Carcione J. M., Seriani G., 1994. Numerical simulation of interface waves by high-order spectral modeling techniques. The Journal of the Acoustical Society of America, 95 (2):681-693. doi: 10.1121/1.408428 Satyam N., Rao K. S., 2009. Estimation of peak ground acceleration for Delhi NCR using FINSIM, a finite fault simulation technique. International Journal of Geotechnics and Environment, 1 (2):147-159. Seriani G., Priolo E., Carcione J. M., et al., 1992. High-order spectral element method for elastic wave modeling. In:Proceedings of the 62th SEG Annual Meeting. New Orleans, Louisiana:Society of Expanded Abstracts, 1285-1288. Shahjouei A., Pezeshk S., 2015. Synthetic seismograms using a hybrid broadband ground-motion simulation approach:application to central and eastern united states. Bulletin of the Seismological Society of America, 105 (2A):686-705. doi: 10.1785/0120140219 Somerville P., Irikura K., Graves R., et al. 1999.Characterizing crustal earthquake slip models for the prediction of strong ground motion. Seismological Research Leteers, 70 (1):59-80. doi: 10.1785/gssrl.70.1.59 Zhou H., Jiang H., 2015. A new time-marching scheme that suppresses spurious oscillations in the dynamic rupture problem of the spectral element method:the weighted velocity Newmark scheme. Geophysical Journal International, 203 (2):927-942. doi: 10.1093/gji/ggv341 Zonno G., Carvalho A., Franceschina G., et al., 2005. Simulating earthquake scenarios using finite-fault model for the Metropolitan Area of Lisbon (MAL). In: Proceedings of the 250th Anniversary of the 1755 Lisbon Earthquake. Portugal, 1-4 November. Zonno G., Carvalho A., 2006. Modeling the 1980 Irpinia earthquake by stochastic simulation. Comparison of seismic scenarios using finite-fault approaches. In: Proceedings of the 1st European Conference on Earthquake Engineering and Seismology. Geneva, Switzerland, 3-8 September. -
下载:
点击查看大图
计量
- 文章访问数: 124
- HTML全文浏览量: 25
- PDF下载量: 12
- 被引次数: 0
