The Measure Against High Frequency Oscillating Instability of Multi-transmitting Formula
-
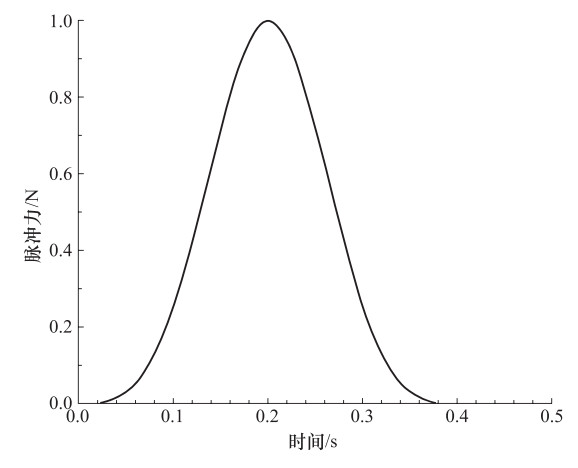
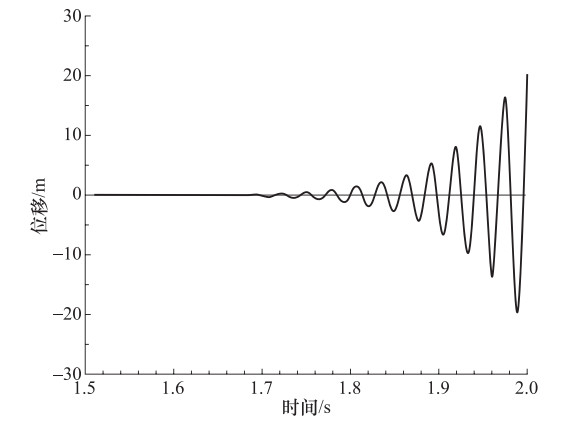
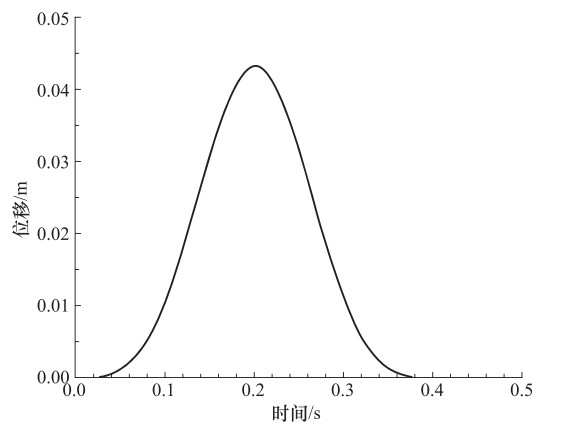
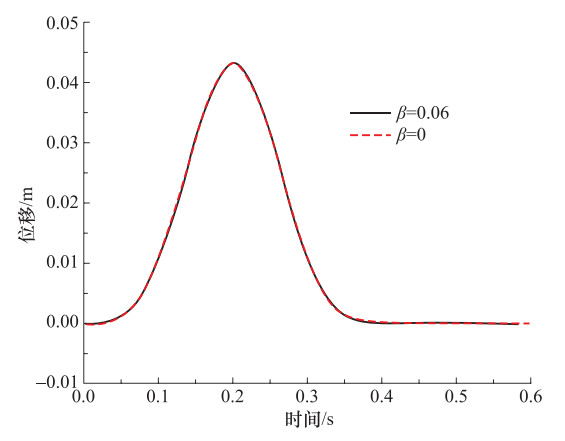
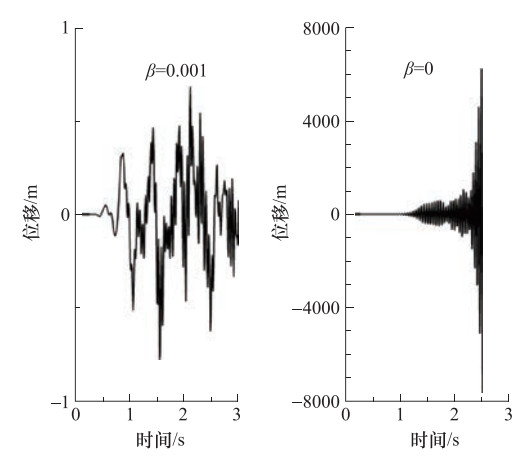
摘要: 多次透射公式（MTF）物理概念简单，便于在计算机上实现时空解藕的高精度波动数值模拟。然而，MTF与其它局部人工边界条件类似，存在数值模拟失稳问题，如高频振荡便是可能出现的失稳现象。本文在分析MTF高频振荡失稳机理的基础上，提出了在波动有限元数值模拟中消除MTF高频振荡失稳的一种措施，即在整个有限元数值模拟区内施加与应变速率成正比的较小粘性阻尼；同时，讨论了这一稳定措施的有效性及其对数值计算精度的影响，并通过数值试验检验了这一稳定措施的可行性。结果表明，消除高频振荡失稳的措施行之有效，且只对波动有限元数值模拟中无意义的高频分量具有抑制作用，而对有意义的较低频段内的波动有限元数值模拟精度影响较小。Abstract: Multi-Transmitting Formula (MTF) based on one-dimensional description on general kinematic characteristics of one-way wave and direct numerical simulation has simple physical concepts, and it is easy to realize the high precision and decoupling wave motion numerical simulation on the computer. However, Multi-Transmitting Formula, similar as other local artificial boundary conditions, is also a local artificial boundary condition which existed numerical instability problems, in which high-frequency oscillation instability is one of the instability phenomenon. Through the discussion of the mechanism of high frequency oscillation instability of Multi-Transmitting Formula, we present a measure to eliminate high frequency oscillation instability in wave numerical simulation. Through numerical simulation, the feasibility of the stabilization measure is verified. The results show that this stabilization measure is effective and of significantly cutting effectiveness on high-frequency component that is meaningless for wave motion numerical simulation. However, its effect on the wave motion numerical simulation was too small to ignore in the lower frequency band.
-
Key words:
- One-way wave /
- Viscous damping /
- Numerical simulation /
- The scattering problem /
- Source problem
-
图 1 MTF数值模拟高频振荡失稳
Figure 1. High-frequency oscillation instability by MTF numerical simulation
图 2 归一化竖向近似脉冲力时程
Figure 2. Time-history of the normalized vertical approximate pulse force
图 3 竖向近似脉冲力作用下作用点处的位移反应时程
Figure 3. The displacement reaction of the point under the normalized vertical approximate pulse force
图 4 引入措施后竖向近似脉冲力作用下作用点处的位移反应时程
Figure 4. The displacement reaction of the point under the normalized vertical approximate pulse force which can eliminate high-frequency oscillation instability
-
关慧敏, 廖振鹏, 1997.一种改善多次透射边界稳定性的措施.地震工程与工程振动, 17(4):1-8. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199700037787 李小军, 唐晖, 2007.结构体系动力方程求解的显式积分格式的能耗特征.工程力学, 24(2):28-33. doi: 10.3969/j.issn.1000-4750.2007.02.005 廖振鹏, 黄孔亮, 杨柏坡等, 1984.暂态波透射边界.中国科学:A辑, 14(6):556-564. doi: 10.1038-nrneph.2009.231/ 廖振鹏, 刘晶波, 1992.波动有限元模拟的基本问题.中国科学:B辑, 22(8):874-882. http://www.cnki.com.cn/Article/CJFDTOTAL-JBXK199208013.htm 廖振鹏, 1996.工程波动理论导引.北京:科学出版社. 廖振鹏, 1997.近场波动的数值模拟.力学进展, 27(2):193-216. http://d.old.wanfangdata.com.cn/Periodical/dzgcygczd200202003 唐晖, 李小军, 李真, 2010.显式积分格式对局部透射边界高频失稳的抑制和消除作用.世界地震工程, 26(4):50-54. http://d.old.wanfangdata.com.cn/Periodical/sjdzgc201004009 谢志南, 廖振鹏, 2008.人工边界高频振荡失稳机理的一点注记.地震学报, 30(3):302-306. doi: 10.3321/j.issn:0253-3782.2008.03.009 杨宇, 李小军, 贺秋梅等, 2014.散射问题中消除多次透射边界高频振荡失稳措施比较分析.地震工程学报, 36(3):476-481. doi: 10.3969/j.issn.1000-0844.2014.03.0476 周正华, 廖振鹏, 2001.消除多次透射公式飘移失稳的措施.力学学报, 33(4):550-554. doi: 10.3321/j.issn:0459-1879.2001.04.015 Liao Z. P., Wong H. L., 1984. A transmitting boundary for the numerical simulation of elastic wave propagation. International Journal of Soil Dynamics and Earthquake Engineering, 3(4):174-183. doi: 10.1016/0261-7277(84)90033-0 Liao Z. P., Liu J. B., 1992. Numerical instabilities of a local transmitting boundary. Earthquake Engineering & Structural Dynamics, 21(1):65-77. doi: 10.1002-eqe.4290210105/ Liao Z. P., 1996. Extrapolation non-reflecting boundary conditions. Wave Motion, 24(2):117-138. doi: 10.1016/0165-2125(96)00010-8 Liao Z. P., 1998. A decoupling numerical simulation of wave motion. Developments in Geotechnical Engineering, 83:125-140. doi: 10.1016/S0165-1250(98)80008-4 -
下载:
点击查看大图
计量
- 文章访问数: 83
- HTML全文浏览量: 8
- PDF下载量: 2
- 被引次数: 0
