Comparative Study of Base Shear Force Method in the Seismic Design Codes of China, the U.S.A. and Europe
-
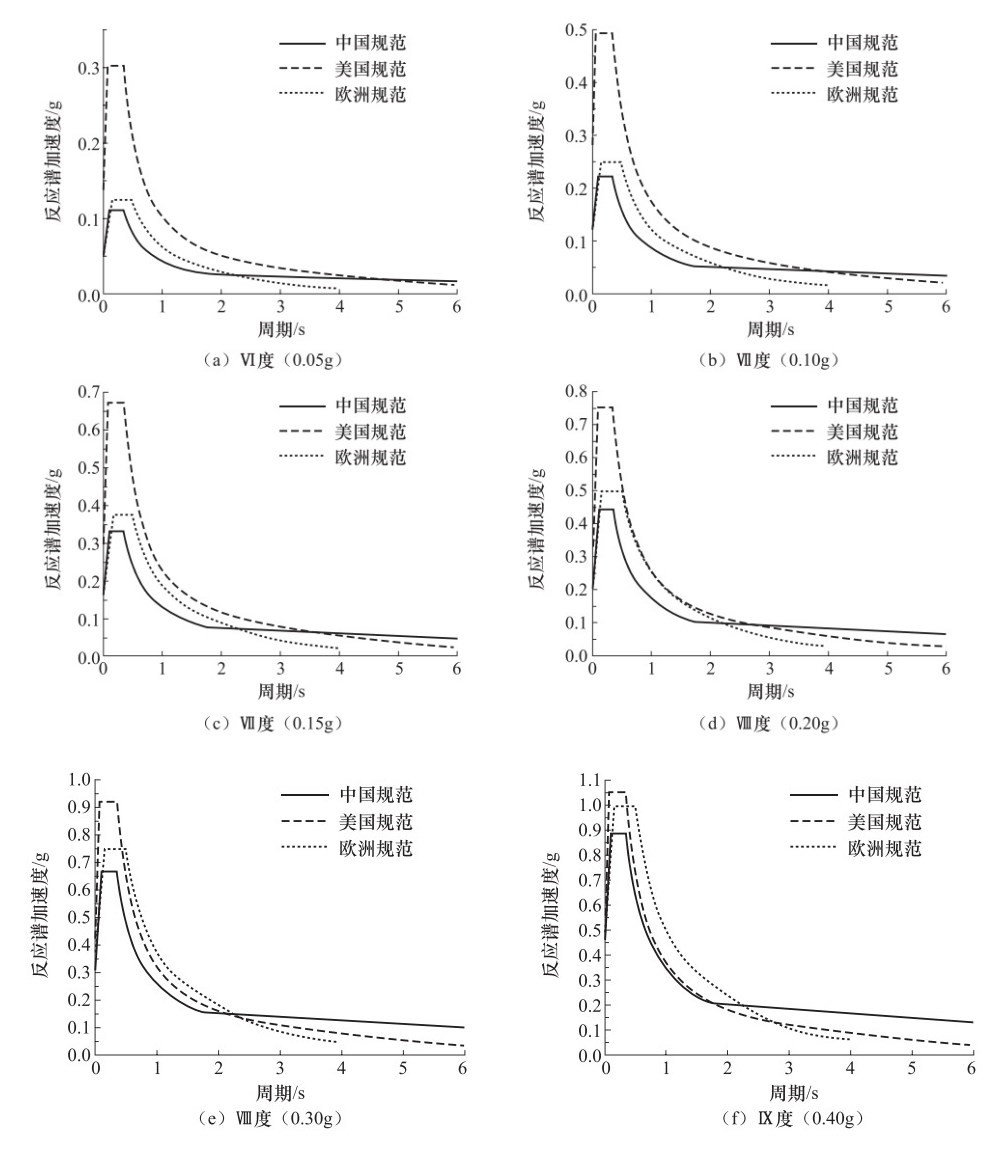
摘要: 目前，底部剪力法是各国计算水平地震作用的基本方法，应用该方法时需要使用各自国家的抗震设计反应谱。本文汇总了中、美、欧抗震设计规范的反应谱和底部剪力法，在相同重现期和场地条件的基础上，对比了不同烈度下3本规范反应谱的异同，并通过算例对比了分别采用3本规范的底部剪力法算出的不同设防烈度下同一结构的底部地震剪力和层间地震剪力。对比结果表明，3本规范的反应谱和底部剪力法在本质上是相同的，只在表达形式和参数设置上存在差异。Abstract: Base shear force method is the basic for calculating the horizontal earthquake action in different countries in the world, and the seismic design response spectrum of each country is needed when using this method. This paper summarizes base shear force method in Chinese, the U.S.A. and European seismic codes. On the basis of the same recurrence period and the same site conditions, the differences and similarities of the three standard response spectra were compared under different intensities. Taking a case study as an example, the earthquake shear forces at the bottom and between the layers are contrasted by using base shear force method in different seismic codes. Our results show that the essence of base shear force method of the three seismic codes from three different countries is similar, while the expression form and parameter settings are different.
-
Key words:
- Seismic design code /
- Response spectrum /
- Base shear force method /
- Seismic action
-
引言
应急演练是指各级人民政府及其部门企业事业单位、社会团体等组织相关单位及人员，依据有关应急预案，模拟应对灾害等突发事件的活动，对以角色扮演、实景模拟或计算机仿真模拟发生的突发事件进行响应和处置，以达到检验应急预案和协调机制、训练专业队伍、开展宣传教育等目的。
2003年应对SARS灾害以来，我国应急管理逐步向现代化发展。南方雨雪冰冻灾害、汶川8.0级地震、“12.31”上海踩踏事件、“8.12”天津港爆炸事故等重特大自然灾害和事故灾难的应对实践，推进了包括预案制定和演练等各项应急相关工作的开展，各级政府、企业事业单位、学校、社区等都开展了应对地震等自然灾害和安全生产事故的多类型应急演练，在一定程度上起到检验预案、完善准备、锻炼队伍、增强意识、提升能力的作用，应急演练已成为应急准备工作的重要环节和例行工作（张媛等，2014）。
社区是社会公共安全治理的基本单元。地震灾害应对实践表明，社区等基层组织在抢救生命、安置群众生活等方面发挥了重要作用。国家综合减灾救灾体制机制改革、国务院应急管理机构改革均要求推进基层自救互救能力和应急管理能力建设，加强对基层民众的自救互救知识培训和科普宣传教育。社区应急演练是提升灾害应对处置能力、开展科普宣传教育并有效提升民众意识的重要途径。近年来，很多社区都开展了针对地震等自然灾害的应急演练，主要内容包括人员疏散、自救互救、人员安置、次生灾害处置等。演练活动通常以实战形式开展，达到了锻炼基层队伍，提升基层组织、社区公众应急处置和防灾减灾意识的目的（张勤等，2014）。但社区地震应急演练仍存在很多问题，在发挥实效性方面存在很大差距，具体表现为：演练方案规划及设计专业程度不足，缺少地震应急领域相关专业的指导；由于涉及人员较多，组织耗时长、难度大，使开展演练的社区数量有限；主要以表演、宣讲的方式开展，针对社区应对灾害组织协调能力等的演练较少，不利于社区应急管理能力的提高；缺乏后续总结、对比、评价等环节，降低了演练实效性；由于社区组织的多样性和复杂性及所处环境的具体性和特殊性，社区应急演练缺乏实战性检验等。
针对上述问题，本文结合传统应急桌面演练及实战演练优势，提出基于在线平台的互联网+社区地震应急桌面演练新模式，并在青海省海西蒙古族藏族自治州（海西州）开展了试点实践，在提升演练专业性、扩大演练社会参与度、提升社区应对地震灾害的组织协调能力等方面取得了初步成效。目前，该模式已成功应用于青海省、江苏省、广州市、徐州市及海西州等20多个省市地区。
1. 互联网+社区地震应急桌面演练平台
互联网+社区地震应急桌面演练模式可实现多地同步联动演练，组织更省时省力，方案设计更灵活多样，由于具有一定的竞技性质，较传统桌面演练更贴近实战，同时该模式可进行全过程记录、评估，大大增强了演练实效性。应急桌面演练平台是在线云平台（图 1），可为应急桌面演练提供零部署、即开即用的实时应急演练服务。该平台基于先进的云服务理念，提供SaaS模式应急演练软件服务，具有较强的伸缩性和灵活性，支持计算机、Pad、手机等多终端应用，并可离线扩展，实现互联网+演练模式。该平台支持包括桌面演练、功能演练、综合演练在内的各种类型演练策划、设计、实施和评估，提供丰富的情景资源库、专业的演练脚本设计工具、全方位的推演过程控制、综合的演练评估工具和评估报告、三维可视化的互动体验，使演练组织者、参与者、观摩人员、评估专家等的深度参与成为可能，有助于提升演练的科学性和有效性，实现演练活动目标（仝鹏，2014）。
2. 海西州演练设计与实施
2018年5月15日至16日，海西州及其下辖市县73个社区管理人员、志愿者队伍负责人及社区民警等180余人采用互联网+社区地震应急桌面演练模式，同步开展不同地域桌面演练活动。演练分为4个时段，连续进行4场。由于演练具有分布式开展、可自行组织参加的便利，海西州各市、县（行委）参演组可根据各自时间安排参加演练。
本次演练定位为使社区相关管理人员进一步熟悉地震应急预案，掌握地震应急工作流程，加强突发事件应变处置及协调指挥能力，增强各种信息分析判断和决策能力，从而使地震等突发事件发生后，社区居民在管理人员的带领和引导下有序开展相关处置工作，有效应对灾害事件。桌面演练准备阶段主要包括演练方案制定、脚本编写、媒体信息制作、参演人员分组、培训等，具体流程如图 2所示。
2.1 演练方案编制
2.1.1 设计演练场景
演练场景设计是对假想事件按其发生过程进行的叙述性说明，即针对假想事件发展过程，设计出一系列突发和次生、衍生事件，让参演人员在演练过程中身临其境，对情景事件变化做出真实的应急反应。
本次演练对象主要为社区管理层及志愿者队伍负责人，为加强对地震灾害的体验和了解，场景设计采用了具有一定破坏性及人员伤亡的灾害背景。设定地震震级为6.5级，震源深度为10km，海西州普遍震感强烈，临近震中区域的城乡结合部发生少量建筑物或构件破坏，并出现人员伤亡情况。部分市政道路、线塔、管道等基础设施受到不同程度影响，局部区域出现供电、供水、供气中断及通信不畅的现象，震中区域附近的化工厂存在危险品泄漏风险。同时，此次地震还会引发大量社会舆论，备受关注，社会稳定面临严峻考验。
2.1.2 演练脚本编写
根据预设地震灾害背景，对地震发生后社区可能出现的真实情况进行设定，包括社区建（构）筑物破坏、通信不畅、物资短缺、人员恐慌、交通堵塞、毒气泄漏、人员伤亡、救援物资及装备短缺等，同时匹配相应的视频、图片、画外音等媒体资源辅助演练（李亦纲等，2007）。
演练脚本主要包括演练信息注入对象、演练事件类别、信息注入时间、事件信息来源及标题、事件信息发生地点、事件信息描述及预期应对方式，具体脚本格式如图 3所示。
图 3 社区地震应急桌面演练脚本（部分）Figure 3. Community earthquake emergency tabletop exercise script(Partial)脚本信息包含的“预期应对方式”是演练方案制定单位以演练脚本为依据，同时结合灾害处置案例及实际工作制定的用于参考的应对答案，“预期应对方式”并不是标准答案，仅供演练后期评估参考使用。
2.2 组织演练培训
培训是桌面演练必不可少的环节，除需对桌面演练整体日程及程序进行介绍外，还需对桌面演练进行详细说明，包括桌面演练的目的意义、演练形式及演练操作系统等，同时需对演练系统进行操作练习，并详细介绍演练所用设施设备用途及使用方法，使所有参演人员提前融入演练场景，正式演练开始后可快速进入角色，全情投入到演练中，令演练效果达到最佳。另外，在培训过程中还需重点强调演练纪律及注意事项，确保演练顺利进行。具体培训内容如图 4所示。
海西州社区地震应急桌面演练由于参演地区较分散，参演人员较多，参演时间不同，无法开展集中式培训，因此采用分散培训的方式。首先，制定桌面演练详细流程图及参演说明，下发至所有参演单位及相关人员，各单位分别开展演练前培训工作，所有技术支持由海西州地震局负责；桌面演练正式开始后，后参演的单位可在演练系统开放时进行操作练习；最后，对于个别有培训需求的参演单位通过在线方式由海西州地震局进行有针对性的培训。
2.3 具体演练流程
桌面演练地点确定并布置完成后，即可按照演练场次安排陆续开展演练。正式演练开始前需先进行身份注册，注册内容包括参演者所在区域、社区名称、社区任职或主要工作及电子邮箱等联系方式。具体演练流程如图 5所示。桌面演练正式开始后，演练系统会定时自动推出事件信息，每条信息推出后所有参演者进行充分讨论，讨论过程中须考虑社区实际情况及参演者自身工作职责。每条事件信息涉及某方面的灾害类型，处置过程中除能了解该灾害类型对社区的影响程度外，还可发现本社区存在的不足及薄弱环节，在制定灾害事件响应措施的同时也可对本社区各项工作方案的制定进行完善。部分参演组由多个社区组成，因此可在讨论中相互学习借鉴。
桌面演练结束后，可在最后环节提交本次演练参与感受及意见、建议，演练评估报告以邮件的方式发给各参演组，作为各社区后续评估总结资料，并永久保留。
3. 演练评估与数据分析
桌面演练数据可在演练全部结束后导出。海西州社区地震应急桌面演练共导出社区地震应急桌面演练应对及评估记录有效数据21套，数据内容主要包括演练场次、时间、演练分组、标题、演练事件内容及应对措施等。数据导出后，针对数据开展分析评估，结合本次演练整体情况完成评估报告，评估报告主要包括本次演练背景、开展情况及评估意见，另附评估记录表，评估记录表（部分）格式如表 1所示。
表 1 海西州社区地震应急桌面演练评估记录（部分）Table 1. Evaluation list of the tabletop exercise in haixi prefecture (Partial)序号 事件标题 事件内容 应对措施 评估结果 1 地震发生 地震发生 及时联系受困人员，进行评估，并上报请求支援，同时进行自救 合格 2 地震造成破坏 某年某月某日，某市发生强烈地震，某社区震感强烈，居民纷纷离开居民楼避震，在社区广场、公园等处聚集，有居民报告人员避震过程中被砸伤。社区部分居民楼等建筑出现不同程度的破坏，有建筑物构件、震碎的玻璃掉落，并发生砸坏车辆、砸伤人员的现象。地震发生在夏天，天气炎热 组织自救互救，保持正常秩序，了解伤亡情况，第一时间上报 优秀 3 楼梯间门扇卡死 有居民报告某栋楼楼梯间门框变形，门扇卡死无法打开，居民无法从楼梯间撤离，亟需帮助 对情况进行评估，同时上报进行救援，了解情况先组织自救 优秀 4 社区居民恐慌 在社区避难场所聚集的居民数量逐渐增加，由于天气炎热，部分老人、孩子出现身体不适，民众情绪出现波动，现场秩序面临失控 及时疏导，做好心理安慰，及时供给饮用水 优秀 本次桌面演练共21个参演组，事件信息应对数量共272条，其中应对优秀200条，占总量的74%，应对合格50条，占总量的18%，无效应对22条，占总量的8%，各组应对情况如图 6所示。
分析表明，此次海西州社区地震应急桌面演练所有参演社区完成了全部演练事件信息的应对任务，处置措施总体情况较好，体现出一定的地震灾害应对能力，但演练过程中也暴露了参演单位及参演者存在的不足，具体问题和改进建议如下：
（1）注意角色定位，社区发挥承上启下的过渡作用，应及时沟通上级和外部支援，专业问题寻求专业支持；
（2）进一步熟悉社区志愿者队伍及相关应急装备情况，未建立队伍的应及早建立，以便自救互救；
（3）明确社区是否制定针对地震灾害的应急预案或相关方案，未制定的尽快制定，并通过开展演练进行检验；
（4）进一步了解社区周边支持保障情况，如物资、视频、队伍支持等；
（5）注意震后社区次生灾害隐患的监控及排查等相关工作；
（6）提高科普宣传教育工作的重视程度，利用挂图等工具向居民普及地震现象、地震灾害、应急避险等知识；
（7）预期应对方式仅作为参考，具体处置措施应视社区实际情况而定。
最终的评估报告包括桌面演练背景、演练现场总体情况、演练总体评价、参演组评估统计表及演练应对与评估记录表。评估报告除包括专业分析评价外，还包括桌面演练原始数据及参演人员应对答案，该报告不仅可作为演练总结评估的依据，还可作为参演单位进行反馈对比的材料。根据评估报告，参演单位可对演练期间未能充分讨论或存有疑义的事件信息重新进行深入讨论，也可根据事件信息应对情况对本单位现有应急预案、工作流程等进行改进和完善，同时还可与其他社区进行横向对比，取长补短（郑通彦等，2014）。
4. 结论
通过开展海西州社区地震应急桌面演练活动，参演人员一致认为互联网+社区地震应急桌面演练模式形式新颖、流程清晰、情景设置针对性强、内容贴近实际，不仅充分体现了各市、县（行委）政府对突发事件应急管理和防震减灾工作的高度重视，更达到了锻炼队伍、检验预案、提升能力的目的，同时展示了社区工作人员良好的精神风貌和地震应急处置能力，对保障海西州公共安全起到了积极作用。
随着经济、社会的不断发展，社区功能不断完善，而社区的作用及需要承担的责任越来越大。为了能更好地应对类似地震的突发事件，加强应急管理意识、提高应急管理能力已成为所有社区必不可少的重要工作之一，而基于互联网的地震应急桌面演练也将成为提高社区地震应急处置能力的重要环节，并将在实践过程中不断发展、提升。
-
图 1 中国规范地震影响系数曲线
α：地震影响系数；αmax：地震影响系数最大值；η1：直线下降段的下降斜率调整系数；γ：衰减指数；Tg：特征周期（s）；η2：阻尼调整系数；T：结构自振周期（s）
Figure 1. Seismic effect coefficient curve in the Chinese code
图 4 不同烈度下中、美、欧抗震规范反应谱对比
Figure 4. Comparison of seismic response spectra among China, the U.S.A. and Europe under different intensities
图 5 中、美、欧基底剪力系数Cs对比
Figure 5. Comparison of base shear coefficient among China, America and Europe
图 6 中、美、欧竖向分配系数Cvi对比
Figure 6. Comparison of vertical distribution coefficient Cvi among China, the U.S.A. and Europe
图 7 中、美、欧层间地震剪力对比
Figure 7. Comparison of seismic shear between layers among China, the U.S.A. and Europe
表 1 水平地震影响系数最大值αmax
Table 1. The coefficients of the maximum horizontal seismic influence αmax
地震影响 Ⅵ Ⅶ Ⅷ Ⅸ 多遇地震 0.04 0.08（0.12） 0.16（0.24） 0.32 罕遇地震 0.28 0.50（0.72） 0.90（1.20） 1.40 注：括号中的数值分别用于设计基本地震加速度为0.15g和0.30g的地区。 
下载: 导出CSV
表 2 特征周期值Tg(s)
Table 2. The value of characteristic period Tg(s)
设计地震分组 场地类别 Ⅰ0 Ⅰ1 Ⅱ Ⅲ Ⅳ 第一组 0.20 0.25 0.35 0.45 0.65 第二组 0.25 0.30 0.40 0.55 0.75 第三组 0.30 0.35 0.45 0.65 0.90
下载: 导出CSV
表 3 场地系数Fa
Table 3. Site Coefficient Fa
场地类别 短周期（0.2s）最大考虑地震反应谱加速度参数 Ss≤0.25 Ss=0.5 Ss=0.75 Ss=1.0 Ss≥1.25 A 0.8 0.8 0.8 0.8 0.8 B 1.0 1.0 1.0 1.0 1.0 C 1.2 1.2 1.1 1.0 1.0 D 1.6 1.4 1.2 1.1 1.0 E 2.5 1.7 1.2 0.9 0.9 F 场地反应分析按特殊场地的地震动确定方法执行 注：对处于中间的Ss，场地系数Fa可按线性插入法取值。
下载: 导出CSV
表 4 场地系数Fv
Table 4. Site Coefficient Fv
场地类别 周期1s最大考虑地震反应谱加速度参数 S1≤0.1 S1=0.2 S1=0.3 S1=0.4 S1≥0.5 A 0.8 0.8 0.8 0.8 0.8 B 1.0 1.0 1.0 1.0 1.0 C 1.7 1.6 1.5 1.4 1.3 D 2.4 2.0 1.8 1.6 1.5 E 3.5 3.2 2.8 2.4 2.4 F 场地反应分析按特殊场地的地震动确定方法执行 注：对处于中间的S1，场地系数Fv可按线性插入法取值。
下载: 导出CSV
表 5 Ⅰ类弹性反应谱的各参数值
Table 5. Values of the parameters of the recommended TypeⅠelastic response spectra
场地类别 S TB/s TC/s TD/s A 1.0 0.15 0.4 2.0 B 1.2 0.15 0.5 2.0 C 1.15 0.20 0.6 2.0 D 1.35 0.20 0.8 2.0 E 1.4 0.15 0.5 2.0
下载: 导出CSV
表 6 Ⅱ类弹性反应谱的各参数值
Table 6. Values of the parameters of the recommended TypeⅡelastic response spectra
场地类别 S TB/s TC/s TD/s A 1.0 0.05 0.25 1.2 B 1.35 0.05 0.25 1.2 C 1.5 0.10 0.25 1.2 D 1.8 0.10 0.30 1.2 E 1.6 0.05 0.25 1.2
下载: 导出CSV
表 7 中、美、欧抗震设防目标
Table 7. Comparison of seismic fortification targets from China, the U.S.A. and Europe
国家或地区 设防目标 50年内超越概率 重现期 中国 小震不坏 63.2% 50年 中震可修 10% 475年 大震不倒 2%—3% 约2000年 美国 倒塌概率极小 2% 2500年 欧洲 破坏极限要求 40% 50年 不倒塌要求 10% 475年
下载: 导出CSV
表 8 中国规范中震对应的水平地震影响系数最大值
Table 8. The maximum horizontal seismic influence coefficient under medium earthquake in the Chinese code
烈度 Ⅵ（0.05g） Ⅶ（0.10g） Ⅶ（0.15g） Ⅷ（0.20g） Ⅷ（0.30g） Ⅸ（0.40g） αmax 0.11 0.22 0.33 0.44 0.67 0.89
下载: 导出CSV
表 9 美国规范的谱加速度参数（C类场地）
Table 9. Spectral acceleration parameters in the U.S.A. standard(Site class C)
参数名称 Ⅵ（0.05g） Ⅶ（0.10g） Ⅶ（0.15g） Ⅷ（0.20g） Ⅷ（0.30g） Ⅸ（0.40g） SS 0.38 0.65 1.01 1.13 1.38 1.58 S1（第一组） 0.09 0.16 0.22 0.25 0.33 0.39 S1（第二组） 0.11 0.18 0.26 0.30 0.39 0.48 S1（第三组） 0.12 0.21 0.30 0.35 0.46 0.55
下载: 导出CSV
表 10 欧洲规范的设计地面加速度ag值（B类场地）（g）
Table 10. The design ground acceleration ag in the European standard(Site class B)(g)
反应谱类别 Ⅵ（0.05g） Ⅶ（0.10g） Ⅶ（0.15g） Ⅷ（0.20g） Ⅷ（0.30g） Ⅸ（0.40g） Ⅰ类 0.042 0.083 0.125 0.167 0.250 0.333 Ⅱ类 0.037 0.074 0.111 0.148 0.222 0.296
下载: 导出CSV
表 11 顶部附加地震作用系数
Table 11. Additional seismic action coefficient at the top
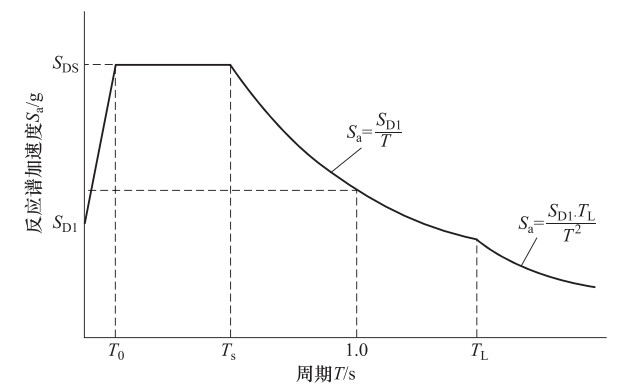
Tg/s T1＞1.4Tg T1≤1.4Tg Tg≤0.35 0.08T1+0.07 0 0.35＜Tg≤0.55 0.08T1+0.01 Tg＞0.55 $ 0.08{\tilde T_1}0.02$
下载: 导出CSV
表 12 中、美、欧规范基底剪力系数
Table 12. Base shear coefficient in the standard of China, the U.S.A. and Europe
比较项 中国 美国 欧洲 底部地震剪力（kN） ${F_{{\rm{Ek}}}} = {\alpha _1}{G_{{\rm{eq}}}} = 0.85{\alpha _1}W$ $V = {C_{\rm{s}}}W$ ${F_{\rm{b}}} = {S_{\rm{d}}}({T_1})\; \cdot \; m\lambda = \lambda {S_{\rm{d}}}({T_1}){\rm{ }}W/{\rm{g}}$ 基底剪力系数Cs ${C_{\rm{s}}} = 0.85{\alpha _1}$ ${C_{\rm{s}}} = \frac{{{S_{{\rm{DS}}}}}}{{(R/{I_{\rm{e}}})}}$ ${C_{\rm{s}}} = \lambda {S_{\rm{d}}}({T_1})/{\rm{g}}$ 注：g为重力加速度。
下载: 导出CSV
表 13 中、美、欧规范基本自振周期T1（10层钢混框架）
Table 13. Basic natural vibration period T1 in the standard of China, the U.S.A. and Europe (A 10-storey reinforced concrete frame)
比较项 中国 美国 欧洲 基本自振周期T估算公式 $T = 0.1n$ $T = {C_t}h_n^x$ $T = {C_t}{H^{3/4}}$ 相关参数 $n = 10$ ${C_t} = 0.0466$
$x = 0.9$
${h_{10}} = 4.2 + 3.6 \times 9 = 36.6\left({\rm{m}} \right)$${C_t} = 0.075$
$H = 4.2 + 3.6 \times 9 = 36.6\left({\rm{m}} \right)$10层钢混框架的基本自振周期T1（s） ${T_1} = 0.1 \times 10 = 1$ ${T_1} = 0.0466 \times {36.6^{0.9}} = 1.190$ ${T_1} = 0.075 \times {36.6^{3/4}} = 1.116$
下载: 导出CSV
表 14 中国规范的基底剪力系数Cs（10层钢混框架）
Table 14. Base shear coefficient Cs in the Chinese standard(A 10-storey reinforced concrete frame)
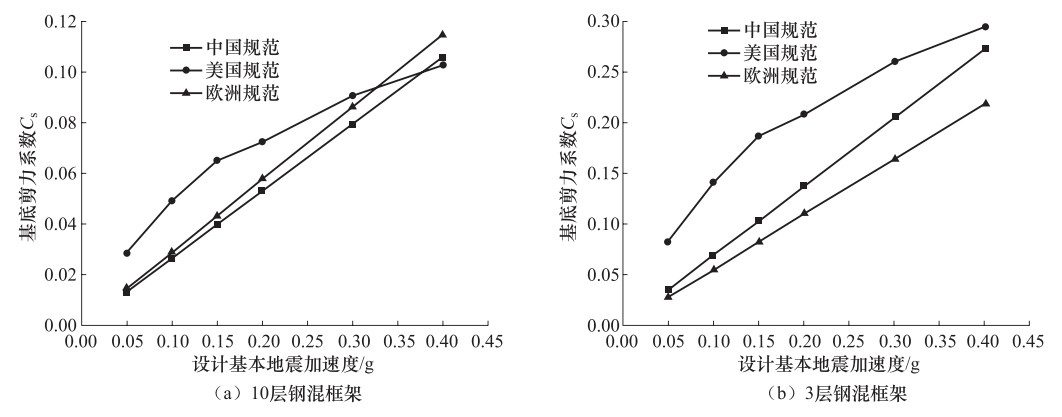
参数 Ⅵ度（0.05g） Ⅶ度（0.10g） Ⅶ度（0.15g） Ⅷ度（0.20g） Ⅷ度（0.30g） Ⅸ度（0.40g） αmax 0.04 0.08 0.12 0.16 0.24 0.32 ${\alpha _1} = {\left({\frac{{{T_g}}}{{{T_1}}}} \right)^{0.9}}{\alpha _{\max }}$ 0.016 0.031 0.047 0.062 0.093 0.124 ${C_{\rm{s}}} = 0.85{\alpha _1}$ 0.013 0.026 0.040 0.053 0.079 0.106 注：根据设计地震分组为第1组，场地类别为Ⅱ类，查得特征周期值Tg=0.35s。
下载: 导出CSV
表 15 美国规范的基底剪力系数Cs（10层钢混框架）
Table 15. Base shear coefficient Cs in the U.S.A. standard(A 10-storey reinforced concrete frame)
参数 Ⅵ度（0.05g） Ⅶ度（0.10g） Ⅶ度（0.15g） Ⅷ度（0.20g） Ⅷ度（0.30g） Ⅸ度（0.40g） Ss 0.38 0.65 1.01 1.13 1.38 1.58 Fa 1.2 1.14 1 1 1 1 S1 0.09 0.16 0.22 0.25 0.33 0.39 Fv 1.7 1.64 1.58 1.55 1.47 1.41 ${S_{{\rm{DS}}}} = 2/3{F_a}{S_{\rm{s}}}$ 0.304 0.494 0.673 0.753 0.920 1.053 ${S_{{\rm{D}}1}} = 2/3{F_v}{S_1}$ 0.102 0.175 0.232 0.258 0.323 0.367 ${T_0} = 0.2{S_{{\rm{D}}1}}/{S_{{\rm{DS}}}}$（s） 0.067 0.071 0.069 0.069 0.070 0.070 ${T_{\rm{s}}} = {S_{{\rm{D}}1}}/{S_{{\rm{DS}}}}$（s） 0.336 0.354 0.344 0.343 0.352 0.348 TL（s） 4 4 4 4 4 4 ${C_{\rm{s}}} = \frac{{{S_{{\rm{DS}}}}}}{{(R/{I_{\rm{e}}})}}$ 0.101 0.165 0.224 0.251 0.307 0.351 $\frac{{{S_{{\rm{D}}1}}}}{{T(R/{I_{\rm{e}}})}}$ 0.029 0.049 0.065 0.072 0.091 0.103 $0.044{S_{{\rm{DS}}}}{I_{\rm{e}}}$ 0.013 0.022 0.030 0.033 0.040 0.046 Cs最终值 0.029 0.049 0.065 0.072 0.091 0.103 注：规范中查得反应谱修正系数R=3，重要性系数Ie=1.0。
下载: 导出CSV
表 16 欧洲规范的基底剪力系数Cs（10层钢混框架）
Table 16. Base shear coefficient Cs in the European standard(A 10-storey reinforced concrete frame)
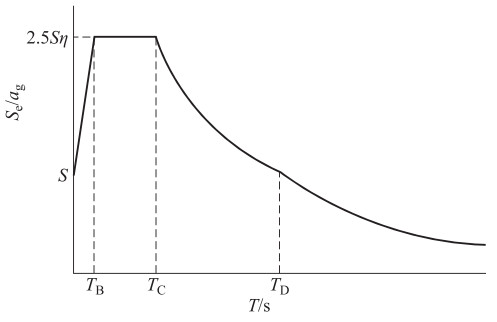
参数 Ⅵ度（0.05g） Ⅶ度（0.10g） Ⅶ度（0.15g） Ⅷ度（0.20g） Ⅷ度（0.30g） Ⅸ度（0.40g） ag/g 0.042 0.083 0.125 0.167 0.250 0.333 ${S_{\rm{d}}}({T_1})/{\rm{g}} = {a_{\rm{g}}}S\frac{{2.5}}{q}\left({\frac{{{T_{\rm{C}}}}}{{{T_1}}}} \right)/{\rm{g}}$ 0.014 0.029 0.043 0.058 0.086 0.115 βag/g 0.008 0.017 0.025 0.033 0.050 0.067 ${C_{\rm{s}}} = \lambda {S_{\rm{d}}}({T_1})/{\rm{g}}$ 0.014 0.029 0.043 0.058 0.086 0.115 注：规范中查得场地土系数S=1.2，TB=0.15s，TC=0.5s，TD=2.0s，β=0.2；性能系数q=3.9；因T1＞2TC，故λ=1.0。
下载: 导出CSV
表 17 中、美、欧规范基本自振周期T1（3层钢混框架）
Table 17. Basic natural vibration period T1 in the standard of China, the U.S.A. and Europe (A 3-storey reinforced concrete frame)
比较项 中国 美国 欧洲 基本自振周期T估算公式 $T = 0.1n$ $T = {C_t}h_n^x$ $T = {C_t}{H^{3/4}}$ 相关参数 $n = 3$ ${C_t} = 0.0466$
$x = 0.9$
${h_3} = 4.2 + 3.6 \times 2 = 11.4\left({\rm{m}} \right)$${C_t} = 0.075$
$H = 4.2 + 3.6 \times 2 = 11.4\left({\rm{m}} \right)$3层钢混框架的基本自振周期T1（s） ${T_1} = 0.1 \times 3 = 0.3$ ${T_1} = 0.0466 \times {11.4^{0.9}} = 0.416$ ${T_1} = 0.075 \times {11.4^{3/4}} = 0.465$
下载: 导出CSV
表 18 中国规范的基底剪力系数Cs（3层钢混框架）
Table 18. Base shear coefficient Cs in the Chinese standard(A 3-storey reinforced concrete frame)
参数 Ⅵ度（0.05g） Ⅶ度（0.10g） Ⅶ度（0.15g） Ⅷ度（0.20g） Ⅷ度（0.30g） Ⅸ度（0.40g） αmax 0.04 0.08 0.12 0.16 0.24 0.32 ${\alpha _1} = {\alpha _{\max }}$ 0.04 0.08 0.12 0.16 0.24 0.32 ${C_{\rm{s}}} = 0.85{\alpha _1}$ 0.034 0.068 0.102 0.136 0.204 0.272
下载: 导出CSV
表 19 美国规范的基底剪力系数Cs（3层钢混框架）
Table 19. Base shear coefficient Cs in the U.S.A. standard(A 3-storey reinforced concrete frame)
参数 Ⅵ度（0.05g） Ⅶ度（0.10g） Ⅶ度（0.15g） Ⅷ度（0.20g） Ⅷ度（0.30g） Ⅸ度（0.40g） ${C_{\rm{s}}} = \frac{{{S_{{\rm{DS}}}}}}{{(R/{I_{\rm{e}}})}}$ 0.101 0.165 0.224 0.251 0.307 0.351 $\frac{{{S_{{\rm{D}}1}}}}{{T(R/{I_{\rm{e}}})}}$ 0.082 0.140 0.186 0.207 0.259 0.294 $0.044{S_{{\rm{DS}}}}{I_{\rm{e}}}$ 0.013 0.022 0.030 0.033 0.040 0.046 Cs最终值 0.082 0.140 0.186 0.207 0.259 0.294 注：其它相关参数与楼层或房屋高度无关，均与10层钢混框架的参数相同，故该表未列出。
下载: 导出CSV
表 20 欧洲规范的基底剪力系数Cs（3层钢混框架）
Table 20. Base shear coefficient Cs in the European standard(A 3-storey reinforced concrete frame)
参数 Ⅵ度（0.05g） Ⅶ度（0.10g） Ⅶ度（0.15g） Ⅷ度（0.20g） Ⅷ度（0.30g） Ⅸ度（0.40g） ag/g 0.042 0.083 0.125 0.167 0.250 0.333 ${S_{\rm{d}}}\left({{T_1}} \right)/{\rm{g}} = {a_{\rm{g}}}S\frac{{2.5}}{q}/{\rm{g}}$ 0.032 0.064 0.096 0.128 0.192 0.256 ${C_{\rm{s}}} = \lambda {S_{\rm{d}}}\left({{T_1}} \right)/{\rm{g}}$ 0.027 0.054 0.082 0.109 0.163 0.218 注：因T1＜2TC，且层数超过2层，故λ=0.85；其它相关参数均与10层钢混框架的参数相同。
下载: 导出CSV
表 21 中、美、欧规范竖向分配系数Cvi
Table 21. The vertical distribution coefficient Cvi in the standard of China, the U.S.A. and Europe
比较项 中国 美国 欧洲 楼层水平地震作用 ${F_i} = \frac{{{G_i}{H_i}}}{{\sum\limits_{j = 1}^n {{G_j}{H_j}} }}{F_{{\rm{Ek}}}}(1 - {\delta _n})$ ${F_x} = {C_{vx}}V = \frac{{{w_x}h_x^k}}{{\sum\limits_{i = 1}^n {{w_i}h_i^k} }}V$ 动力分析方法：${F_i} = {F_{\rm{b}}}\frac{{{s_i}{m_i}}}{{\sum {s_j}{m_j}}}$ 近似计算方法：${F_i} = {F_{\rm{b}}}\frac{{{z_i}{m_i}}}{{\sum {z_j}{m_j}}}$ 竖向分配系数Cvi ${C_{vi}} = \frac{{{G_i}{H_i}}}{{\sum\limits_{j = 1}^n {{G_j}{H_j}} }}(1 - {\delta _n})$ ${C_{vi}} = \frac{{{w_i}h_i^k}}{{\sum\limits_{j = 1}^n {{w_j}h_j^k} }}$ 动力分析方法：${C_{vi}} = \frac{{{s_i}{m_i}}}{{\sum {s_j}{m_j}}}$ 近似计算方法：${C_{vi}} = \frac{{{z_i}{m_i}}}{{\sum {z_j}{m_j}}}$ 相关参数 ${\delta _n} = 0.08{T_1} + 0.07 = 0.15$ $k = 1.69$
下载: 导出CSV
-
曹继涛, 2013.中美欧规范钢筋混凝土框架结构抗震设计对比研究.西安: 西安建筑科技大学. 胡聿贤, 2006.地震工程学.北京:地震出版社. 蒋志楠, 2010.我国建筑抗震规范中部分条款的演变及与欧美规范的对比探讨.哈尔滨: 中国地震局工程力学研究所. 李国强, 李杰, 陈素文等, 2014.建筑结构抗震设计.4版.北京:中国建筑工业出版社. 李慧, 2011.中、美、欧、日建筑抗震规范地震作用对比研究.哈尔滨: 哈尔滨工业大学. 罗开海, 王亚勇, 2006.中美欧抗震设计规范地震动参数换算关系的研究.建筑结构, 36(8):103-107. http://www.cnki.com.cn/Article/CJFDTOTAL-JCJG200608027.htm 孙景江, 2006.建筑结构抗震研究若干基本问题概述及讨论.震灾防御技术, 1(2):87-96. doi: 10.3969/j.issn.1673-5722.2006.02.001 王亚勇, 郭子雄, 吕西林, 1999.建筑抗震设计中地震作用取值——主要国家抗震规范比较.建筑科学, 15(5):36-39, 55. http://www.cnki.com.cn/Article/CJFDTOTAL-JZKX199905016.htm 叶列平, 方鄂华, 2009.关于建筑结构地震作用计算方法的讨论.建筑结构, 39(2):1-7. doi: 10.3321/j.issn:1000-6869.2009.02.001 中华人民共和国住房和城乡建设部, 2012.建筑结构荷载规范(GB 50009-012).北京:中国建筑工业出版社. 中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2010.建筑抗震设计规范(GB 50011-2010).北京:中国建筑工业出版社. American Society of Civil Engineers, 2010. ASCE/SEI7-10 Minimum design loads for buildings and other structures. Reston, VA: American Society of Civil Engineers. European committee for Standardization, 2004. Eurocode 8: Design of structures for earthquake resistance-Part 1: General rules, seismic actions and rules for buildings. Brussels: European Committee for Standardization. -
下载:
点击查看大图
计量
- 文章访问数: 130
- HTML全文浏览量: 252
- PDF下载量: 37
- 被引次数: 0
