Seismic Fragility Analysis of RC Frame Structure Based on Energy Balance
-
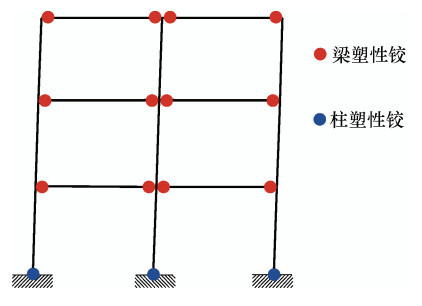
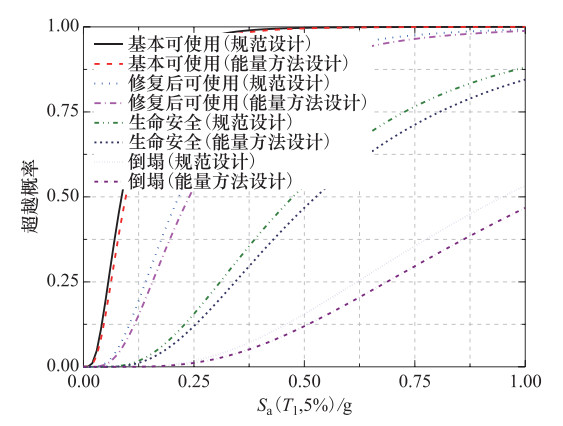
摘要: 基于“强柱弱梁”的屈服机制，依据能量平衡方法设计了某6层RC框架结构，采用震级-震中距条带地震动记录选取方法，选取12条随机地震动，利用Perform-3D有限元分析软件对结构进行增量动力（IDA）分析，得到了结构的地震易损性曲线、破坏状态概率曲线以及结构破坏概率矩阵。分析结果表明：该方法设计的结构能够形成预设的“强柱弱梁”屈服机制，可以保证结构中梁充分参与耗能，同时结构具有较强的抗倒塌能力，可以满足“小震不坏，中震可修，大震不倒”的性能要求。Abstract: The energy-based seismic design method of RC framed structure of the "strong column with weak beam" was proposed, and 6 layer RC frame structures were designed by selecting ground motion records using magnitude epicentral distance strips in this paper. We selected 12 ground motions and analyzed the RC frames structure through the IDA method by Perform-3D, and obtained the seismic fragility curves, failure probability curves and the structural failure probability matrices. The results showed that the structure designed by this method can form the preset "strong column with weak beam" yielding mechanism. It makes promise that the beam in the structure is fully involved in energy dissipation with strong anti-collapse capacity, not only can satisfy fully operational level under frequent earthquake and fulfill reparably operational level under rare earthquake, but also satisfy near collapse level under extremely rare earthquakes.
-
图 4 最大层间位移角与Sa（T1，5%）关系
Figure 4. Relationship between maximum inter story drift angle and Sa(T1, 5%)
图 5 层间位移角概率密度分布图
Figure 5. Probabilitic density distributing diagram of drift angle between layers
图 8 梁、柱弹塑性应变能所占比例
Figure 8. The proportion of elastic plastic strain energy of beam and column
表 1 12条地震动记录
Table 1. Records of 12 seismic waves
地震动 台站 震级MW 震中距R/km 峰值加速度aPGA/g Northridge Beverly Hills-14145 Mulhol 6.7 13.39 0.416 Cape Mendocino Rio Dell Overpass-FF 7.1 22.64 0.549 Superstition Hills Poe Road(temp) 6.5 11.2 0.45 Loma Prieta Capitola 6.9 15.2 0.53 Duzce, Turkey Bolu 7.1 41.27 0.728 Friuli，Italy Tolmezzo 6.5 15.8 0.35 Imperial Valley Delta 6.5 22 0.35 Northridge Canyon Country-WLC 6.7 12.4 0.48 San Fernando LA-Hollywood 6.5 22.8 0.21 Superstition Hills El Centro Imp.Co. 6.5 18.2 0.36 Hector Mine Hector 7.1 11.7 0.34 Kocaeli Turkey Duzce 7.1 15.4 0.36 
下载: 导出CSV
表 2 不同性能状态下层间位移角限值
Table 2. Definition of drift angle between layers in different performance states
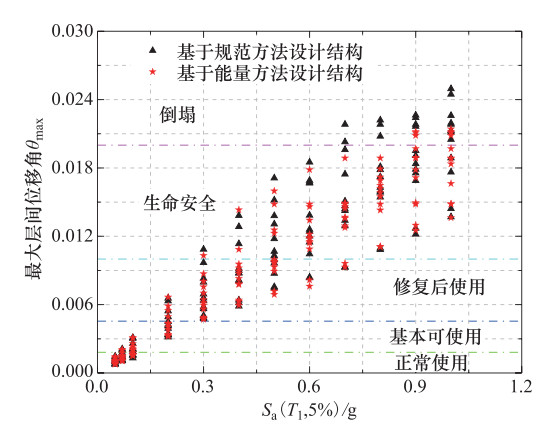
正常使用 基本可使用 修复后使用 生命安全 倒塌 [θ]≤1/550 1/550＜[θ]≤1/220 1/220＜[θ]≤1/100 1/100＜[θ]≤1/50 [θ]＞1/50
下载: 导出CSV
表 3 楼（屋）面荷载、结构构件参数
Table 3. Roof load and sizes of main structural members
楼层 柱/mm×mm 梁/mm×mm 恒载/kN·m-2 活载/kN·m-2 1-3 600×600 300×600 5.5 3.5 4-5 500×500 250×500 5.5 3.5 6 500×500 250×500 6.5 0.5
下载: 导出CSV
表 4 结构破坏概率矩阵
Table 4. Damage probability matrix of the structure
地震水准${S_a}({T_1}, \xi)$/g 性能水平/% 正常使用 基本可使用 修复后使用 生命安全 倒塌 能量方法设计 规范设计 能量方法设计 规范设计 能量方法设计 规范设计 能量方法设计 规范设计 能量方法设计 规范设计 多遇地震 87.39 86.6 12.61 13.4 0 0 0 0 0 0 设防地震 12.19 9.18 61.15 54.73 19.92 26.79 6.31 8.61 0.43 0.69 罕遇地震 1.2 0.76 20.82 13.59 18.89 20.8 55.97 60.62 3.12 4.23
下载: 导出CSV
-
白久林, 欧进萍, 2012.基于能量平衡的钢筋混凝土框架结构抗震塑性设计方法.建筑结构学报, 33(10):22-31. http://d.old.wanfangdata.com.cn/Periodical/jzjgxb201210004 白久林, 金双双, 欧进萍, 2017.防屈曲支撑-钢筋混凝土框架结构基于能量平衡的抗震塑性设计.建筑结构学报, 38(1):125-134. http://d.old.wanfangdata.com.cn/Periodical/jzjgxb201701014 陈昉健, 易伟建, 2015.近场地震作用下锈蚀钢筋混凝土桥墩的IDA分析.湖南大学学报(自然科学版), 42(3):1-8. http://d.old.wanfangdata.com.cn/Periodical/hndxxb201503001 龚思礼, 2003.建筑抗震设计手册.北京:中国建筑工业出版社. 黄悠越, 2012.基于构件性能的RC框架结构层间位移角性能指标限值研究.广州:华南理工大学. 李刚, 程耿东, 2004.基于性能的结构抗震设计——理论、方法与应用.北京:科学出版社. 缪志伟, 马千里, 叶列平, 2013.钢筋混凝土框架结构基于能量抗震设计方法研究.建筑结构学报, 34(12):1-10. http://d.old.wanfangdata.com.cn/Periodical/jzjgxb201312001 缪志伟, 叶列平, 2014.钢筋混凝土框架-剪力墙结构基于能量抗震设计方法的耗能需求计算与设计流程.建筑结构学报, 35(1):10-18. http://d.old.wanfangdata.com.cn/Periodical/jzjgxb201401002 施炜, 叶列平, 陆新征等, 2011.不同抗震设防RC框架结构抗倒塌能力的研究.工程力学, 28(3):41-48, 68. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201100215417 叶列平, 缪志伟, 程光煜等, 2014.建筑结构基于能量抗震设计方法研究.工程力学, 31(6):1-12, 20. http://cdmd.cnki.com.cn/Article/CDMD-10703-1015037045.htm 叶列平, 马千里, 缪志伟, 2009.结构抗震分析用地震动强度指标的研究.地震工程与工程振动, 29(4):10-22. http://d.old.wanfangdata.com.cn/Periodical/dzgcygczd200904002 中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2010.GB 50011-2010建筑抗震设计规范.北京:中国建筑工业出版社. 中华人民共和国住房和城乡建设部, 2011.GB 50010-2010混凝土结构设计规范.北京:中国建筑工业出版社. ATC-63, 2008. Quantification of building seismic performance factors ATC-63 Project Report-90% Draft FEMA P695/April 2008. Redwood City, California: Applied Technology Council. Erberik M. A., Elnashai A. S., 2004. Fragility analysis of flat-slab structures. Engineering Structures, 26(7):937-948. doi: 10.1016/j.engstruct.2004.02.012 FEMA 356, 2000. Prestandard and commentary for the seismic rehabilitation of buildings. Washington, DC: Federal Emergency Management Agency. Housner G. W., 1956. Limit design of structures to resist earthquakes. In: Proceedings of the 1st World Conference on Earthquake Engineering. Oakland, Calif: Earthquake Engineering Research Institute, 1-12. Leelataviwat S., Goel S. C., Stojadinović B., 2002. Energy-based seismic design of structures using yield mechanism and target drift. Journal of Structural Engineering, 128(8):1046-1054. doi: 10.1061/(ASCE)0733-9445(2002)128:8(1046) Liao W. C., 2010. Performance-based plastic design of earthquake resistant reinforced concrete moment frames. Michigan:University of Michigan, 39-47. doi: 10.1007%2Fs11803-013-0181-1 -
点击查看大图
计量
- 文章访问数: 55
- HTML全文浏览量: 5
- PDF下载量: 4
- 被引次数: 0
