A Wavelet Comprehensive Threshold Seismic Signal Denoising Method
-
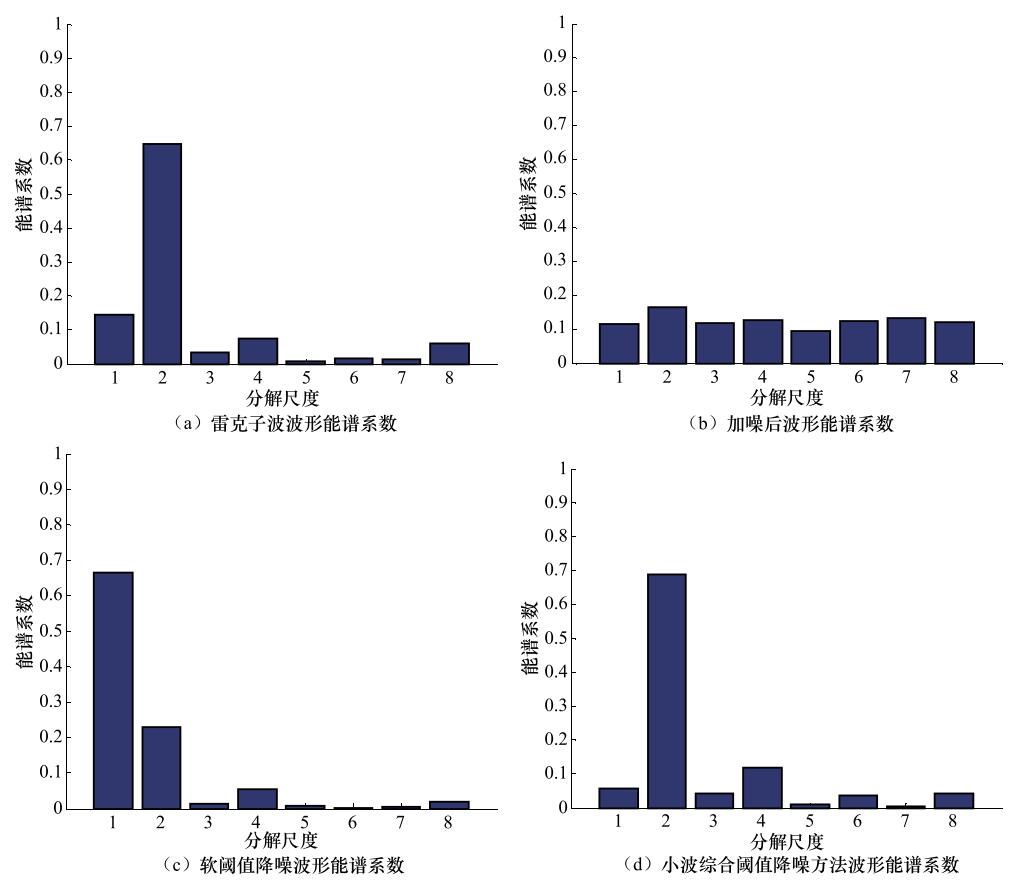
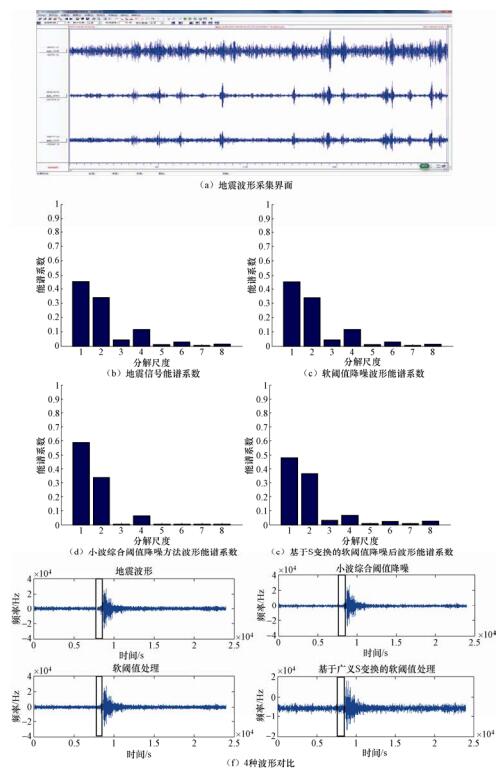
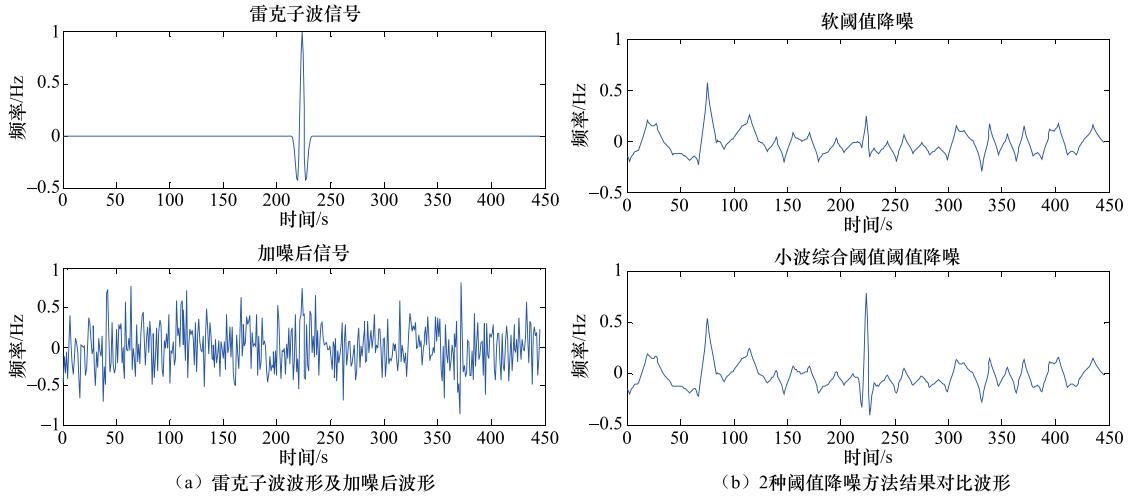
摘要: 小波阈值方法中硬、软阈值方法是地震信号降噪常用方法，但容易造成信号中高频信息丢失导致地震误判和漏判情况发生。小波综合阈值方法继承和发展了硬、软阈值降噪方法的优点，对信号高频部分用硬阈值方法，以提高高频信号能量，对信号低频部分用软阈值方法，提高信号降噪能力的同时保证信号连续性和光滑性。利用噪声信号小波系数小和地震信号小波系数大的特征，进行雷克子波降噪仿真实验和实际地震信号降噪实验。仿真实验表明，小波综合阈值方法降噪后波形MSE值最小，且降噪后与原信号波形最近似，降噪后波形高频部分能量增强且抑制低频部分能量。最后，对实际采集的地震信号进行降噪处理，处理后信号中能量增强被压制，利用处理后的信号可得到地震的初至时间。Abstract: The wavelet threshold method with hard or soft threshold is common for noise reduction of seismic signal, but it is often to cause the loss of high frequency information in the signal to lead in earthquake misjudgment or missing judgment. Taking the advantages of hard threshold and soft threshold denoising method, the wavelet comprehensive threshold improves the high frequency signal energy by the hard threshold treatment, and keeps the signal smoothness and reduce the signal degradation of noise capacity while ensuring signal continuity by lowness of the signal. Based on the small wavelet coefficients of the noise signal and the large wavelet coefficients of the seismic signal, the simulation experiment of the Ricker signal and the noise reduction experiment is carried out. The simulation results show that the MSE of the wavelet comprehensive threshold is the closest to the original signal waveform after noise reduction, and the energy of the high frequency part of the waveform is reduced and the low frequency part is suppressed. Finally, taking the noise reduction of the natural waveform as an example, we found that noise signal energy is suppressed and the first time of the waveform can be obtained.
-
Key words:
- Comprehensive threshold /
- Seismic signal /
- Wavelet method
-
图 2 雷克子波波形图及降噪方法能谱系数
Figure 2. Ricker wavelet and energy-spectrum coefficient of noise reduction method
图 3 逊母口镇软阈值处理图及降噪方法对比图
Figure 3. Comparison of seismic waveforms with different noise reduction methods in Xunmukou county
表 1 噪声分类
Table 1. Noise classification
噪声类型 频率范围/Hz 降噪难度 环境噪声 3—20 难 次生噪声 5—30 难 仪器噪声 1—2 易 
下载: 导出CSV
表 2 仿真降噪后所得结果的SNR和MSE值
Table 2. SNR and MSE from the de-noised signal in simulation
降噪方法 SNR MSE 硬阈值 18.5736 0.2907 软阈值 19.3285 0.2897 小波综合阈值 19.4136 0.2784
下载: 导出CSV
-
耿冠世, 俞言祥, 2015.中国西部地区震源破裂尺度与震级的经验关系.震灾防御技术, 10(1):68-76. doi: 10.11899/zzfy20150107 侯跃伟, 赵兵, 田韬, 2015.基于Daubechies小波分析的南京数字化钻孔形变震前变化特征研究.震灾防御技术, 10(2):388-396. doi: 10.11899/zzfy20150219 孔祥茜, 吴继伟, 岳继光, 2005.地震信号小波变换的去噪方法.计算机辅助工程, 14(3):52-56. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjfzgc200503012 范涛, 赵兆, 吴海, 2014.矿井瞬变电磁多匝回线电感影响消除及曲线偏移研究.煤炭学报, 39(05):932-940. http://www.oalib.com/paper/4232079 刘霞, 潘洪屏, 高晓春, 2010.基于小波阈值的地震信号去噪处理.科学技术与工程, 10(29):7251-7254. doi: 10.3969/j.issn.1671-1815.2010.29.030 李英, 张淑贞, 许康生, 2006.小波降噪方法在地震信号处理中的应用.西北地震学报, 28(2):159-162. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=xbdzxb200602013 曲中党, 吴蔚, 贺日政等, 2015.基于S变换的软阈值滤波在深地震反射数据处理中的应用.地球物理学报, 58(9):3157-3168. doi: 10.6038/cjg20150912 唐守锋, 童敏明, 潘玉祥等, 2011.煤岩破裂微震信号的小波特征能谱系数分析法.仪器仪表学报, 32(7):1521-1527. http://www.cnki.com.cn/Article/CJFDTOTAL-YQXB201107012.htm 魏学强, 袁洪克, 秦晶晶等, 2016.广义S变换地震信号时频分析.震灾防御技术, 11(4):808-813. doi: 10.11899/zzfy20160411 曾宪伟, 赵卫明, 师海阔等, 2010.利用小波包变换对地震信号进行时频分析时小波基函数的选取.地震研究, 33(4):323-328. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dzyj201004012 郑作亚, 卢秀山, 李克行, 2007.一类小波基函数的构造及其在测量数据处理中的应用探讨.测绘科学, 32(3):9-11. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_chkx200703003 Bruni V., Vitulano D., 2006. Wavelet-based signal de-noising via simple singularities approximation. Signal Processing, 86(4):859-876. doi: 10.1016/j.sigpro.2005.06.017 Mousavi S. M., Langston C. A., 2016. Hybrid seismic denoising using higher-order statistics and improved wavelet block thresholding. Bulletin of the Seismological Society of America, 106(4):1380-1393. doi: 10.1785/0120150345 Xia L. M., Zheng W., Liang M. D., 2017. Application of a comprehensive one dimensional wavelet threshold denoising algorithm in blasting signal. In: Balas V. E., Jain L. C., Zhao X. M., Information Technology and Intelligent Transportation Systems. Cham: Springer, 517-527. -
点击查看大图
图(3) / 表(2)
计量
- 文章访问数: 53
- HTML全文浏览量: 5
- PDF下载量: 4
- 被引次数: 0
