Variation Characteristics of Long Period Gravity Field in Southwestern Tianshan
-
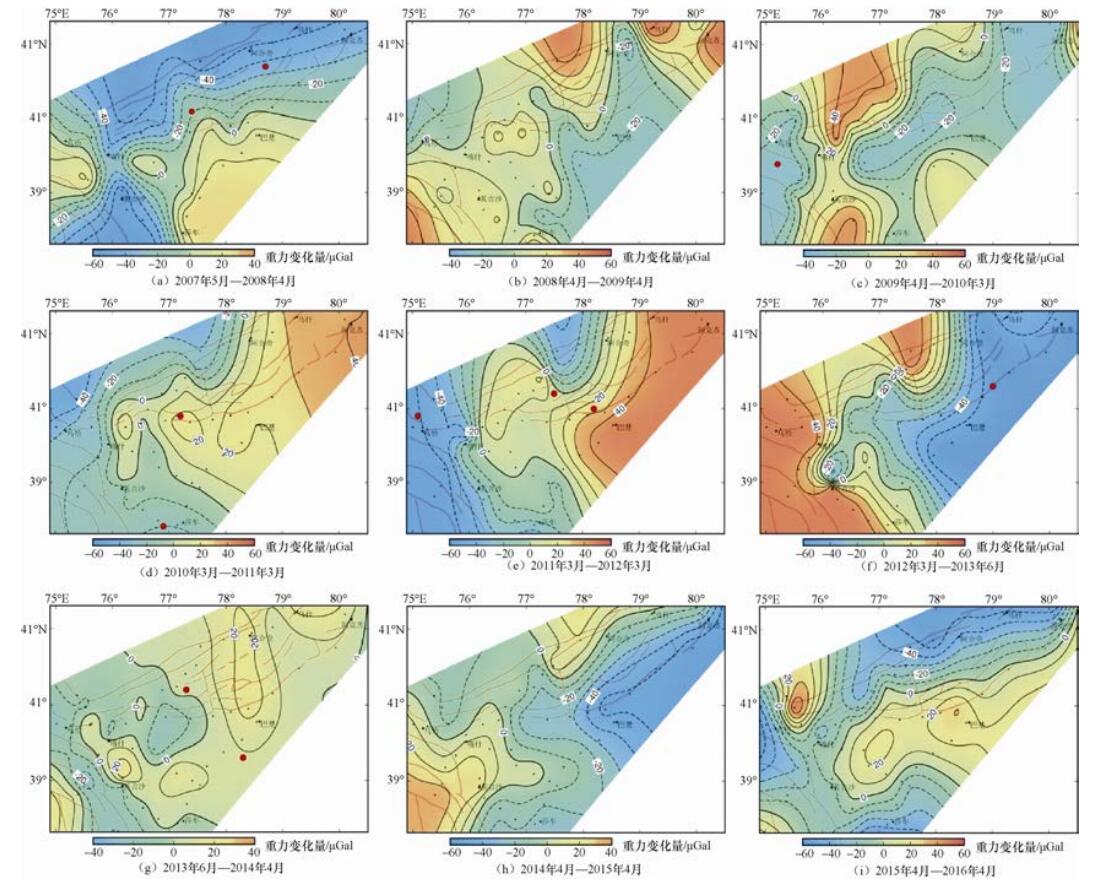
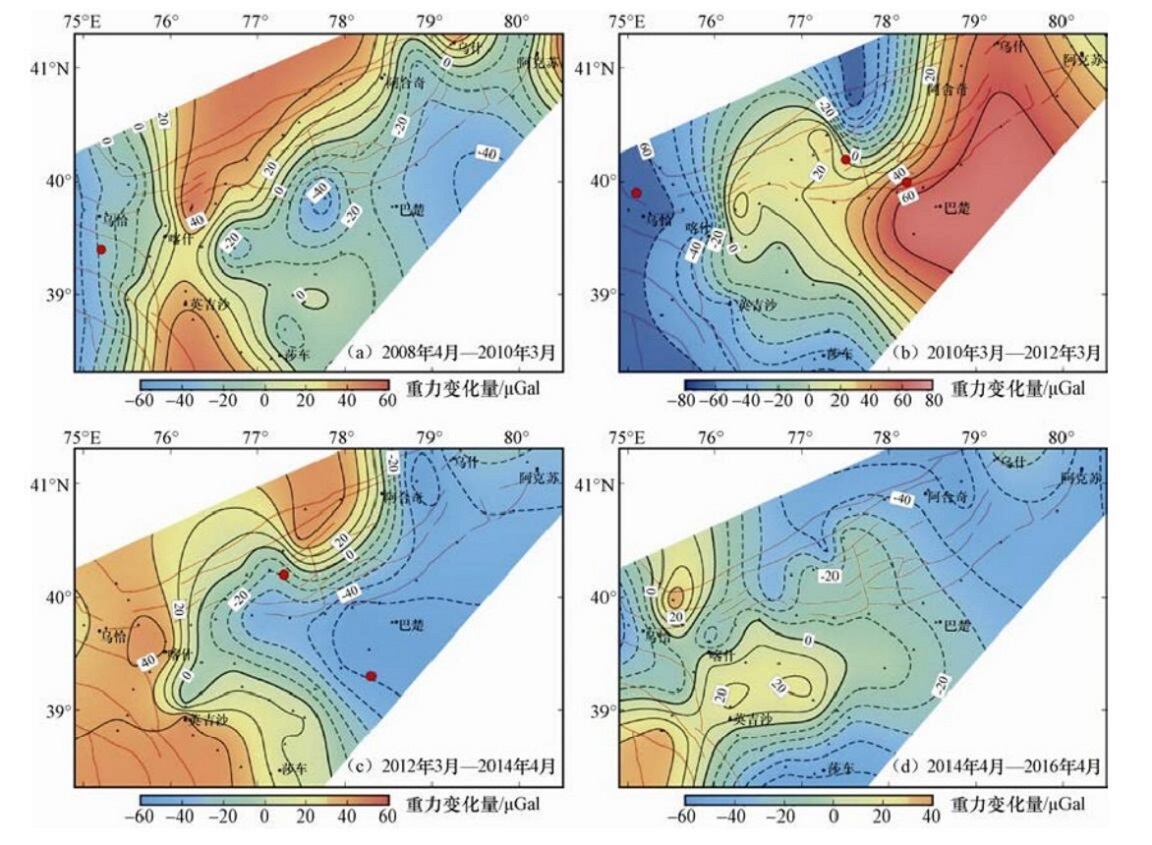
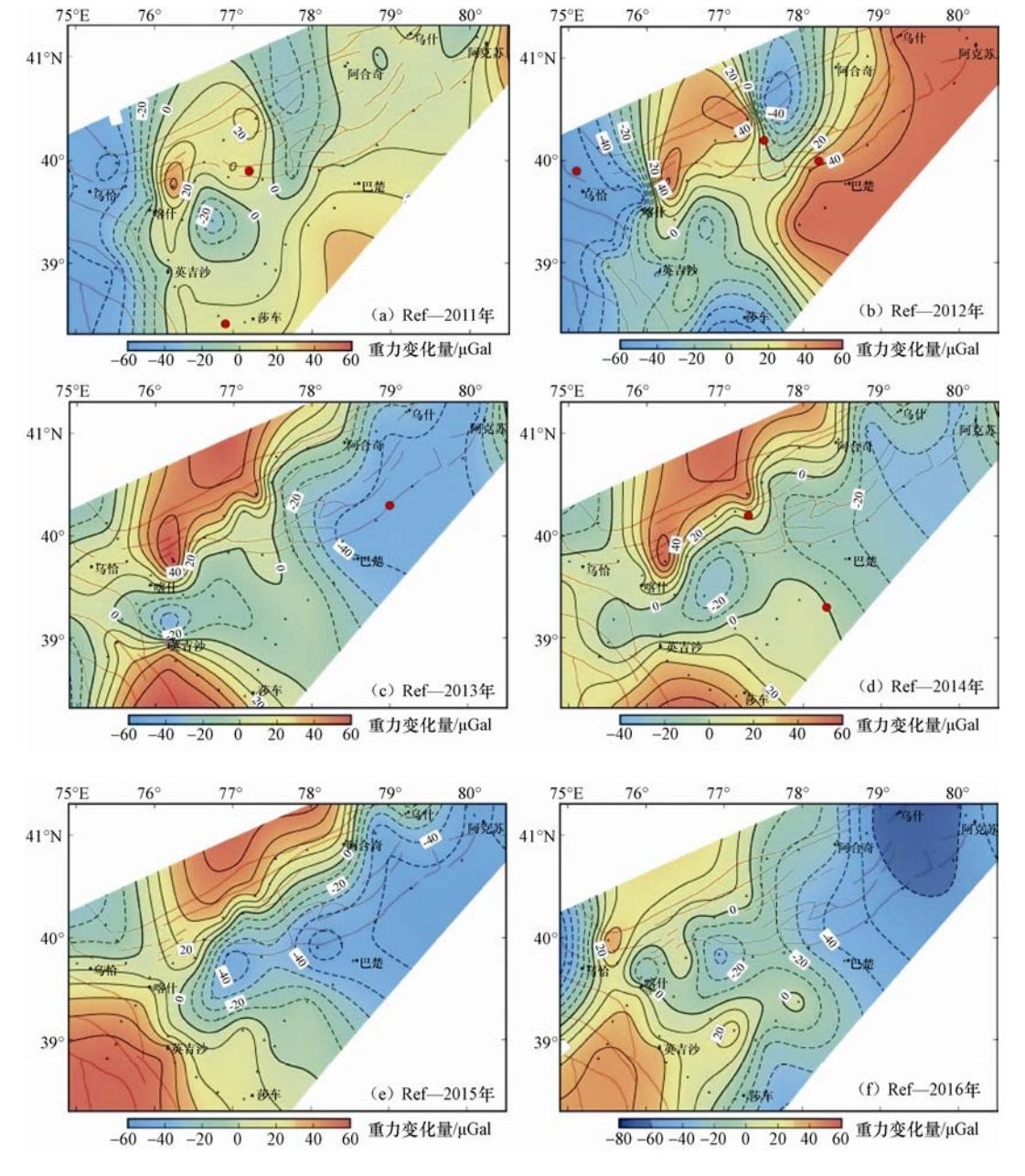
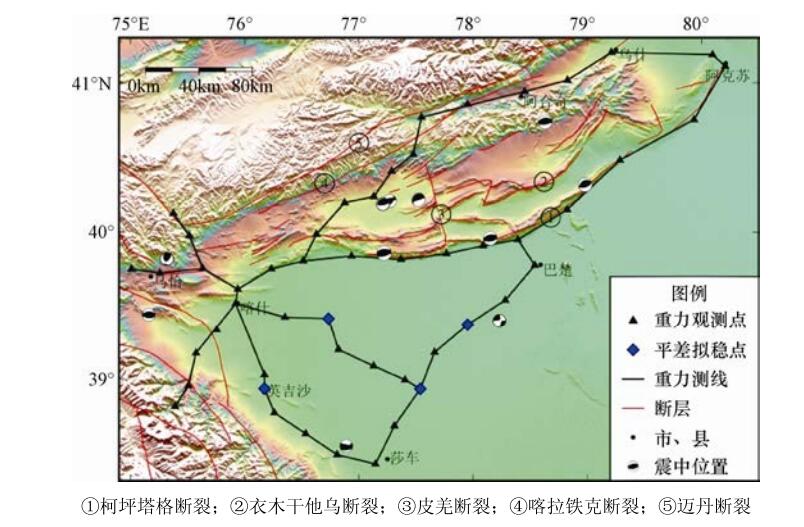
摘要: 利用西南天山地区2007至2016年共20期流动重力观测资料，分析该地区一年、两年尺度和累积重力变化特征，探讨区域构造活动、地震孕育发生与重力场变化特征的关系。结果表明：西南天山地区迈丹断裂带、柯坪塔格断裂带等大型断裂带影响该区域的重力场分布，使该地区较多出现NEE向的重力梯度分布特征。塔里木盆地和西南天山重力变化有明显的差异性，2个不同的构造块体在重力分布上呈现相对反向变化，塔里木盆地和西南天山地区的重力变化界线不在塔里木盆地边缘的山前地带，而较多出现在柯坪推覆体中北缘地带。西南天山地区的地震大部分发生在重力正值变化区域的零线附近，震中及附近地区重力异常分布与构造特征有较好的一致性。在活动断裂带附近同时出现重力变化零线以及与断裂走向一致的重力变化高梯度带，可作为中短期前兆异常。Abstract: By using the 20-year data observed from 2007 to 2016, we analyzed the gravitational variations characteristics of in one and two year scale in the southwestern Tianshan area, in order to study the relationship between gravitational field changes to structural features, generation and occurrence of earthquakes. Our results show that the regional faults such as Maidan fault and Kepingtage fault, have great effect on the gravitational field distribution in southwestern Tianshan area, resulting in the preferred NEE direction of gravitational gradient distribution. There exists obvious difference of gravitational change between northwestern Tianshan and Tarim basin, in which the two different structural blocks have opposite changes in gravitational field. The boundary of gravitational change between Tarim basin and southwestern Tianshan mostly lays on the middle-north part of Keping nappe instead of in the edge of Tarim basin. There exists a consistency between gravitational anomalies and structural distribution where the earthquakes in the southwestern Tianshan area mainly along the positive gravity change zone with near zero line. Such local anomalies can be taken as the mediate-short term precursor of earthquakes in the region.
-
Key words:
- Southwestern Tianshan /
- Mobile gravity /
- Gravitational anomaly
-
引言
众所周知，我国是地震频发的国家，地震可能造成高速铁路列车脱轨事故，为此，我国建立了相应的地震报警及紧急处置系统，力争在潜在破坏性地震到达之前发出报警，降低列车发生脱轨或倾覆的概率。目前广泛采用的地震报警参数主要为峰值加速度PGA，然而PGA主要体现地震波幅值，未考虑频谱及持时影响，对于无破坏性的高频小震可能产生误报现象。为避免这种干扰，郭恩栋等（2015）引入谱强度SI作为高速铁路地震报警参数，并给出相应的计算方法，SI从能量方面出发，考虑了幅值及频谱影响，忽略持时的影响，但相比PGA更合理。美国电力研究所EPRI（O'Hara 等，1991）在核电厂地震监测报警中引入累积绝对速度CAV作为报警参数，研究发现低频震动对CAV的贡献明显高于高频震动。我国三代核电站AP1000参考国外标准也引入了CAV作为地震报警参数（胡进军等，2013）。林宜娴（2002）提出CAV、PGA、PGV等参数可作为地震报警参数，其稳定性好，且确定性较高。Kostov（2005）根据欧洲几次强地震动数据，分析得出标准化累积绝对速度CAVSTD在预测地震动破坏能力方面明显优于PGA。伊斯坦布尔在地震预报警系统中利用累积绝对速度快速判别强地震动（Erdik等，2003）。Fahjan等（2011）在地震报警的触警算法中引入CAV，并提出新的用于报警系统的参数。黄俊等（2014）引入CAV作为报警参数，分析其在高速铁路报警中的适用性，研究发现CAV可有效排除破坏性小的高频小震对高速铁路列车地震报警的干扰。目前虽对CAV在地震报警中的应用有了深入研究，但在高速铁路列车地震报警中的研究较少，仅通过相关的地震波数据处理得出，未考虑车轨动力响应关系，且给出的计算参数为CAVSTD，为此，需探讨考虑车轨关系的基于相关起算阈值的CAV计算方法。
1. CAV相关参数
目前，地震工程界主要研究CAV、CAVSTD、CAV5。其中CAV于1988年由美国电力研究所（O'Hara等，1991）在核电厂报警中第2级判别标准中提出的，其概念为记录地震加速度数据的绝对值对记录时间进行积分，记为累积绝对速度CAV：
$${\rm{ CAV}} = \mathop \int \nolimits_0^{{{{t}}_{{\rm{max}}}}} \left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t$$ (1) 为提高CAV在核电厂报警中的准确度，EPRI在报告中引入标准化累积绝对速度CAVSTD，其可有效避免长持时记录的地震波尾部对应的幅值小且破坏性小的地震动对其数值的影响，其定义如下：将记录的加速度时程分成以1 s为时间间隔的N个小段，当1 s时间段内存在加速度绝对值≥0.025 g时，对该秒内加速度数值的绝对值进行积分，否则该秒内的积分值记为零，然后将整个记录时程进行相加求和，表达式为：
$$ {\rm{CA{V_{STD}}}} = \mathop \sum \limits_{{i=1}}^n \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\left| {{{a}}\left( {{t}} \right)} \right| < 0.025\;g}\\ {1,\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.025\;{{g}}} \end{array}} \right.$$ (2) Kramer等（2002）于2002年提出CAV5，用于场地液化判别，其概念为：将记录的加速度时程中对加速度数值的绝对值≥0.005 g进行积分求和，表达式为：
$${{\rm{ CAV}}_5} = \displaystyle\int \nolimits_0^\infty \left\langle {\rm{\chi }} \right\rangle \left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\left\langle {\rm{\chi }} \right\rangle = \left\{ {\begin{array}{*{20}{c}} {0\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.005\;g}\\ {1\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.005\;{{g}}} \end{array}} \right. $$ (3) 式中，a(t)为加速度时程，Wi为权重。
2. 改进的标准化累积绝对速度应用于高速铁路地震报警阈值中的计算方法
2.1 改进的标准化累积绝对速度起算阈值确定
本文引入31自由度的SY97477车辆模型（崔恩文，2014），结合车轨典型非线性接触关系，依据列车安全行驶的3项评判指标（脱轨系数、轮重减载率及横向力)，分析车体在轨道不平顺（我国高速铁路无砟轨道标准谱）与简谐波（仅考虑横向输入，与列车行驶方向垂直）共同激励下的动态响应，考虑95%的安全保证，引入2.55倍的动力放大系数（孙汉武等，2007），计算安全极限状态（超出3项指标任意1个限值）下不同车速对应的简谐波幅值随周期的变化关系，如图1所示。具体模型参数、车轨接触关系及评判标准可参考崔恩文（2014）的研究。
图 1 列车安全运行极限状态下不同车速对应的简谐波幅值随周期的变化关系Figure 1. The relationship between the amplitude of simple harmonic wave corresponding to different speeds and periods under the safe running limit state of the train由图1可知，车速一定时，即使幅值很小（<0.025 g）的低频简谐波也可能使列车脱轨，因此不能简单地套用标准化累积绝对速度CAVSTD计算公式，有必要研究改进的标准化累积绝对速度应用在高速铁路地震报警阈值中的计算方法。车速一定时，简谐波幅值随周期增加逐渐递减，最终趋于常数，且周期越大，不同车速对应的简谐波幅值之间的差值越小。车速为200 km/h时，当简谐波周期达2.2 s时，其幅值开始趋于常数，该常数约为0.008 g，本文规定此时的周期为简谐波幅值趋于常数对应的起始周期Tst，该常数记为Amin。不同车速下简谐波幅值趋于常数对应的起始周期及该常数的数值如表1所示。
表 1 不同车速下简谐波幅值趋于常数对应的起始周期及该常数的数值Table 1. The initial period of the simple harmonic wave amplitude tending to be constant at different speeds and the value of the constant项目 车速/（km·h−1） 200 250 300 350 400 起始周期Tst/s 2.2 2.3 2.1 2.0 1.7 Amin/g 0.008 0.004 0.004 0.004 0.004 由表1可知，车速为200 km/h与车速≥250 km/h时对应的Amin不同，车速≥250 km/h时Amin相同，但起始周期Tst随车速的增加呈递减趋势，说明车速越大，简谐波趋于常数所需的周期越小。
车速为200 km/h时，幅值低于0.008 g的简谐波对列车运行安全的影响可忽略不计。车速≥250 km/h时，幅值低于0.004 g的简谐波对列车运行安全的影响可忽略不计。由此可推算出改进的标准化累积绝对速度起算阈值，如表2所示。
表 2 不同车速下改进的标准化累积绝对速度起算阈值Table 2. Starting threshold of improved calculation of standardized cumulative absolute velocity at different speeds项目 车速/（km·h−1） 200 ≥250 改进的标准化累积绝对速度起算阈值/g 0.008 0.004 2.2 改进的标准化累积绝对速度应用在地震报警中的可行性分析
考虑改进的标准化累积绝对速度为累积过程的算法，其值对于加速度超过0.004 g或0.008 g的有限个数的高频小震会很小，因此，可较好地排除高速铁路沿线的高频小震，是较好的地震监测报警参数。
魏智祥（2015）分析了京武高速铁路线布置的强震仪监测到的列车运行时震动记录数据，发现列车运行产生的震动记录明显高于背景噪声，且发现东西、南北、垂直方向列车振动噪声幅值均≤0.002 g，由此可知本文设定的不同车速下改进的标准化累积绝对速度可有效排除列车振动的影响。
综上所述，本文给出改进的标准化累积绝对速度用于高速铁路地震报警是可行的。
2.3 改进的标准化累积绝对速度计算公式的确定
参照CAVSTD计算方法，本文给出车速为200 km/h时改进的标准化累积绝对速度CAV8计算公式如下：
$${{\rm{CAV}}_8} = \mathop \sum \limits_{i=1}^n \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.008\;g}\\ {1,\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.008\;{{g}}} \end{array}} \right.$$ (4) 当
$ a\left(t\right) $ $< 0.008\;g$ 时，${{W}}_{{i}}$ =0；当$\left|{a}\left({t}\right)\right|\geqslant 0.008\;g$ 时，${{W}}_{{i}}$ =1。本文给出的CAV8定义为：将加速度时程按1 s为时间间隔进行划分，如果在这1 s内加速度绝对值≥0.008 g，则对该秒内的加速度绝对值进行积分，否则忽略该秒内的积分值，然后将整个时程中每秒积分得到的数值进行累积求和。
车速为250 km/h时改进的标准化累积绝对速度CAV4计算公式如下：
$${ {\rm{CAV}}_4} = \mathop \sum \limits_{i=1}^{{n}} \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.004\;g}\\ {1,\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.004\;{{g}}} \end{array}} \right.$$ (5) 当
${a}\left({t}\right)$ $< 0.004\;g$ 时，${{W}}_{{i}}=0$ ；当$\left|{a}\left({t}\right)\right|\geqslant 0.004\;{g}$ 时，${{W}}_{{i}}$ =1。本文给出的CAV4定义为：将加速度时程按1 s为时间间隔进行划分，如果在这1 s内加速度绝对值≥0.004 g，则对该秒内的加速度绝对值进行积分，否则忽略该秒内的积分值，然后将整个时程中每秒积分得到的数值进行累积求和。
3. 高速铁路地震报警阈值确定
为确定基于改进的标准化累积绝对速度高速铁路地震报警阈值，本文从Peer数据库选取6条不同场地地震波（表3），对应的加速度反应谱如图2所示，对其进行归一化处理，分析加速度幅值与评判列车脱轨3项指标之间的关系，确定不同车速下影响行车安全的6条地震波加速度上限值，按照本文给出不同车速下改进的标准化累积绝对速度计算公式，给出6条地震波对应的改进的标准化累积绝对速度上限值，如表4所示。
表 3 地震波相关信息Table 3. Seismic wave information项目 地震波台站名称 Cape Mendocino TCU045 Capitola Hector EL Centro Imp. Co. Cent Poe Road 震级 7.01 7.62 6.93 7.13 6.54 6.54 峰值加速度/g 0.376 5 0.008 1 0.528 5 0.265 6 0.357 9 0.446 3 v30/（m·s−1） 567.78 704.64 288.62 726.00 192.05 316.64 加速度记录持时/s 36.0 45.0 39.9 45.3 40.0 22.3 表 4 不同车速下6条地震波加速度上限值与改进的标准化累积绝对速度上限值Table 4. The upper limit of acceleration amplitudes and upper limit improved calculation of standardized cumulative absolute velocity CAV of six seismic waves at different speeds地震波台站名称 车速200 km/h 车速250 km/h 车速300 km/h 车速350 km/h 车速400 km/h 加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-secCape Mendocino 0.074 0.17 0.070 0.17 0.055 0.13 0.040 0.09 0.039 0.09 TCU045 0.101 0.55 0.090 0.49 0.078 0.43 0.062 0.34 0.039 0.21 Capitola 0.109 0.34 0.078 0.25 0.062 0.20 0.054 0.17 0.039 0.11 Hector 0.101 0.27 0.070 0.19 0.062 0.17 0.054 0.14 0.047 0.12 EL Centro Imp. Co. Cent 0.078 0.16 0.070 0.18 0.054 0.13 0.039 0.08 0.027 0.05 Poe Road 0.074 0.19 0.054 0.14 0.043 0.11 0.039 0.10 0.035 0.08 由表4可知，车速相同时，即使地震波加速度相同，其对应的改进的标准化累积绝对速度不一定相同，如车速为200 km/h时，台站名称为Cape Mendocino与Poe Road的地震波加速度相同，但对应的改进的标准化累积绝对速度不同，且Cape Mendocino台站加速度记录持时较大，说明改进的标准化累积绝对速度与频谱紧密相关。车速≥250 km/h时，对于同一台站的地震波，峰值加速度越大其对应的改进的标准化累积绝对速度越大，如台站名称为Cape Mendocino的地震波，说明对于同一地震波而言，加速度影响累积绝对速度。根据改进的标准化累积绝对速度定义，加速度记录持时影响其数值。综上所述，改进的标准化累积绝对速度数值不仅与加速度幅值有关，还与频谱及加速度记录持时密切相关，可较好地反映地震动三要素。
选取6条地震波改进的标准化累积绝对速度最小值作为报警阈值，给出不同车速下基于改进的标准化累积绝对速度高速铁路地震报警阈值，如表5所示。由表5可知，改进的标准化累积绝对速度报警阈值与车速整体呈线性递减关系，中间车速对应的改进的标准化累积绝对速度可按线性插入计算。
表 5 不同车速下改进的标准化累积绝对速度高速铁路地震报警阈值Table 5. High-speed earthquake alarm threshold based on improved calculation of standardized cumulative absolute velocity thresholds at different vehicle speeds项目 车速/（km·h−1） 200 250 300 350 400 报警阈值/g-sec 0.16 0.14 0.11 0.08 0.05 4. 结论
（1）通过建立车轨模型，分析列车安全运行极限状态下简谐波幅值与周期的关系，得出不同车速下改进的标准化累积绝对速度起算阈值，并论证改进的标准化累积绝对速度在高速铁路地震报警中的可行性。
（2）参照标准化累积绝对速度CAVSTD计算公式，本文给出不同车速下改进的标准化累积绝对速度计算公式。
（3）根据本文给出的改进的标准化累积绝对速度计算公式，选取6条不同场地的地震波，分析列车在轨道不平顺及地震波共同激励下的动力响应，计算不同车速下改进的标准化累积绝对速度报警阈值，以供参考。
-
图 1 西南天山重力观测网分布与历史地震
Figure 1. Distribution of gravity observation network and historical earthquakes in southwestern Tianshan
图 3 西南天山地区两年尺度重力场变化等值线图
Figure 3. Two-year scale gravity changes in southwestern Tianshan
表 1 西南天山地区5级以上地震（2007—2016年）
Table 1. Earthquakes with M≥5.0 in southwestern Tianshan (from 2007 to 2016)
发震时间 经度/°E 纬度/°N 震级/M 震源深度/km 地点 2009年2月20日 78.7 40.7 5.2 6 柯坪县 2009年4月22日 77.4 40.1 5.0 7 阿图什市 2011年1月1日 75.2 39.4 5.1 10 乌恰县 2011年8月11日 77.2 39.9 5.8 8 阿图什市、伽师县交界 2011年2月1日 76.9 38.4 5.2 10 莎车县 2012年6月1日 75.1 39.9 5.0 7 乌恰县 2012年8月11日 78.2 40.0 5.2 9 阿图什市 2013年3月11日 77.5 40.2 5.2 8 阿图什市 2013年2月1日 79.0 40.3 5.3 9 柯坪县 2014年7月9日 78.3 39.3 5.1 8 麦盖提县 2015年1月10日 77.3 40.2 5.0 10 阿图什市 
下载: 导出CSV
-
艾力夏提·玉山, 刘代芹, 李杰等, 2014.新疆南天山地区重力场动态变化特征研究.内陆地震, 28(2):176-181. http://www.cnki.com.cn/Article/CJFDTOTAL-LLDZ201402012.htm 陈杰, 丁国瑜, Burbank D. W.等, 2011.中国西南天山山前的晚新生代构造与地震活动.中国地震, 17(2):134-155. http://www.cnki.com.cn/Article/CJFDTOTAL-ZGZD200102003.htm 陈建波, 2008. 新疆地震构造特征研究. 兰州: 中国地震局兰州地震研究所, 1-122. 陈石, 祝意青, 蒋长胜等, 2011.新疆于田MS7.3地震前重力场变化的质源体特征.地震地磁观测与研究, 32(5):1-8. https://www.cs.cmu.edu/afs/cs.cmu.edu/project/cmt-40/Nice/Transfer/Chinese/wikilex-20070908-zh-en.txt 陈运泰, 顾浩鼎, 卢造勋, 1980.1975年海城地震与1976年唐山地震前后的重力变化.地震学报, 2(1):21-31. http://mall.cnki.net/magazine/Article/DZXB198001001.htm 邓起东, 冯先岳, 张培震等, 2000.天山活动构造.北京:地震出版社, 1-399. 董云书, 2010. 西南天山阔克萨勒岭地区蛇绿岩中的基性岩岩石学和地球化学研究. 北京: 中国地质大学(北京), 10-11. 贾民育, 詹洁晖, 2000.中国地震重力监测体系的结构与能力.地震学报, 22(4):360-367. http://www.cnki.com.cn/Article/CJFDTOTAL-DZXB200004003.htm 刘代芹, 李杰, 王晓强等, 2014.新疆及邻近地区重力场变化特征研究.地震工程学报, 36(2):331-337. http://www.cnki.com.cn/Article/CJFDTotal-ZBDZ201402020.htm 刘启元, 陈九辉, 李顺成等, 2000.新疆伽师强震群区三维地壳上地幔S波速度结构及其地震成因的探讨.地球物理学报, 43(3):356-365. http://manu39.magtech.com.cn/Geophy/CN/abstract/abstract3707.shtml 闵伟, 宋方敏, 韩竹军等, 2006.柯坪塔格断裂西段古地震初步研究.地震地质, 28(2):234-244. http://mall.cnki.net/magazine/article/DZDZ200602006.htm 沈军, 陈建波, 王翠等, 2006.2003年2月24日新疆巴楚-伽师6.8级地震发震构造.地震地质, 28(2):205-212. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dzdz200602004 王晓强, 李杰, 朱治国等, 2007.伽师及其邻近地区重力场动态演化特征初步分析.内陆地震, 21(3):213-217. http://www.cnki.com.cn/Article/CJFDTOTAL-LLDZ200703004.htm 于湘伟, 雷建设, 石耀霖等, 2010.西南天山地区的地震重定位与活动性分析.中国科学院研究生院学报, 27(3):350-355. http://www.cqvip.com/QK/97442X/201003/36088199.html 祝意青, 胡斌, 张永志, 1999.永登5.8级地震前后的重力场动态图像特征研究.地壳形变与地震, 19(1):71-77. http://www.cnki.com.cn/Article/CJFDTOTAL-DKXB901.010.htm 祝意青, 江在森, 陈兵等, 2001a.南北地震带和青藏块体东部重力场演化与地震特征.中国地震, 17(1):56-69. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgdz200101007 祝意青, 陈兵, 张希等, 2001b.景泰5.9级地震前后的重力变化研究.中国地震, 17(4):356-363. http://mall.cnki.net/magazine/Article/DZXB1992S1014.htm 祝意青, 胡斌, 朱桂芝等, 2003.河西地区重力场及其动态演化特征.大地测量与地球动力学, 23(4):44-48. http://www.cqvip.com/QK/95685A/200304/8718488.html 祝意青, 李铁明, 郝明等, 2016.2016年青海门源MS6.4地震前重力变化.地球物理学报, 59(10):3744-3752. doi: 10.6038/cjg20161019 Allen M. B., Vincent S. J., Wheeler P. J., 1999. Late Cenozoic tectonics of the Kepingtage thrust zone:Interactions of the Tien Shan and Tarim Basin, Northwest China. Tectonics, 18(4):639-654. doi: 10.1029/1999TC900019 Fu G. Y., Sun W. K., 2008. Surface coseismic gravity changes caused by dislocations in a 3-D heterogeneous earth. Geophysical Journal International, 172(2):479-503. doi: 10.1111/gji.2008.172.issue-2 Okubo S., 1991. Potential and gravity changes raised by point dislocations. Geophysical Journal International, 105(3):573-586. doi: 10.1111/gji.1991.105.issue-3 Sun W., 2004. Short note:Asymptotic theory for calculating deformations caused by dislocations buried in a spherical earth-gravity change. Journal of Geodesy, 78(1-2):76-81. -
下载:
点击查看大图
计量
- 文章访问数: 124
- HTML全文浏览量: 10
- PDF下载量: 5
- 被引次数: 0
