Analysis on Mechanism of Dujiangyan Earthquake Swarm in the Vicinity of Zipingpu Reservoir
-
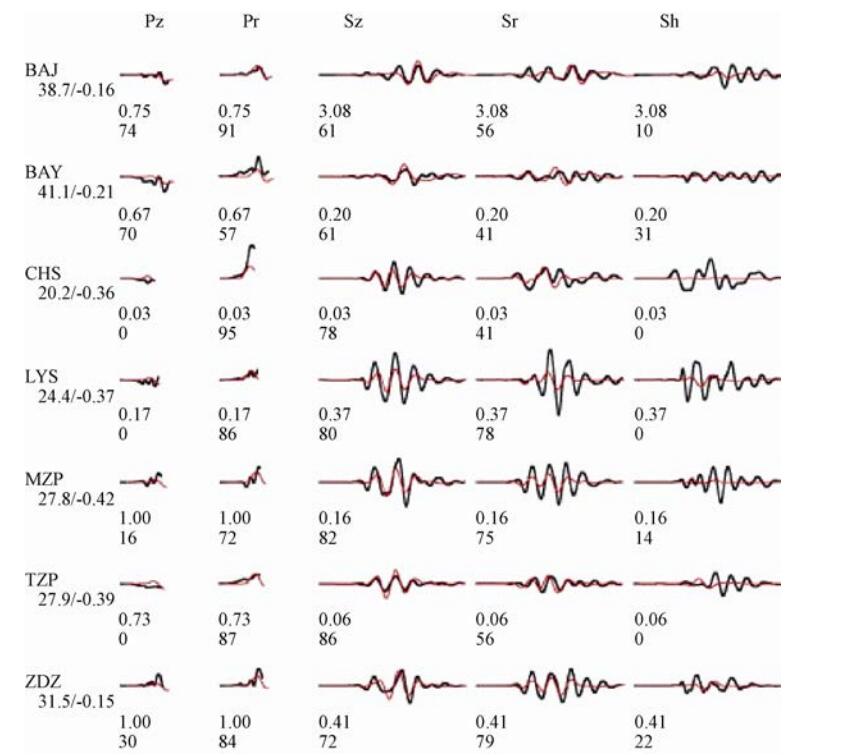
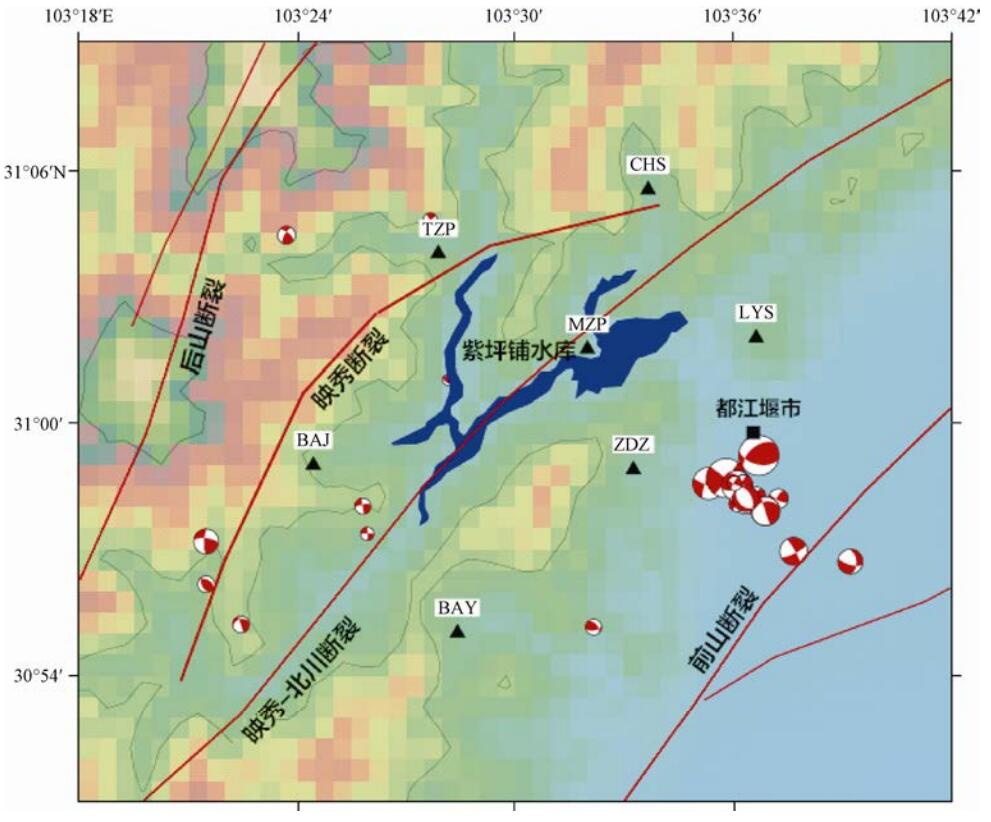
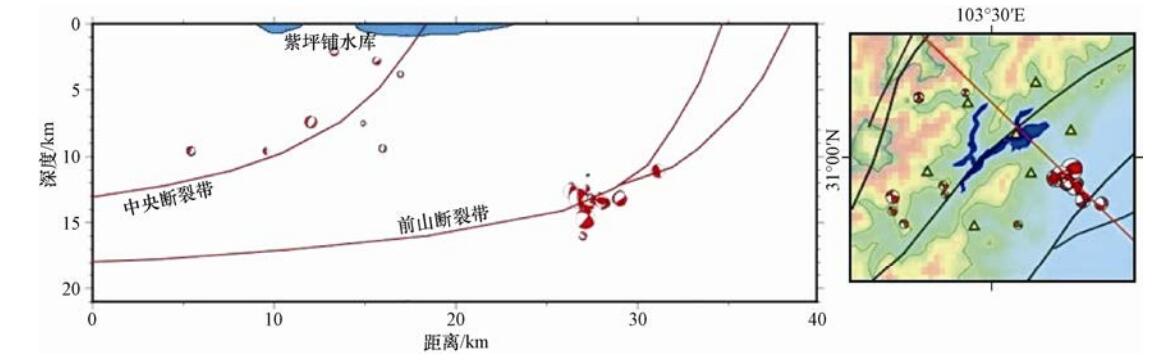
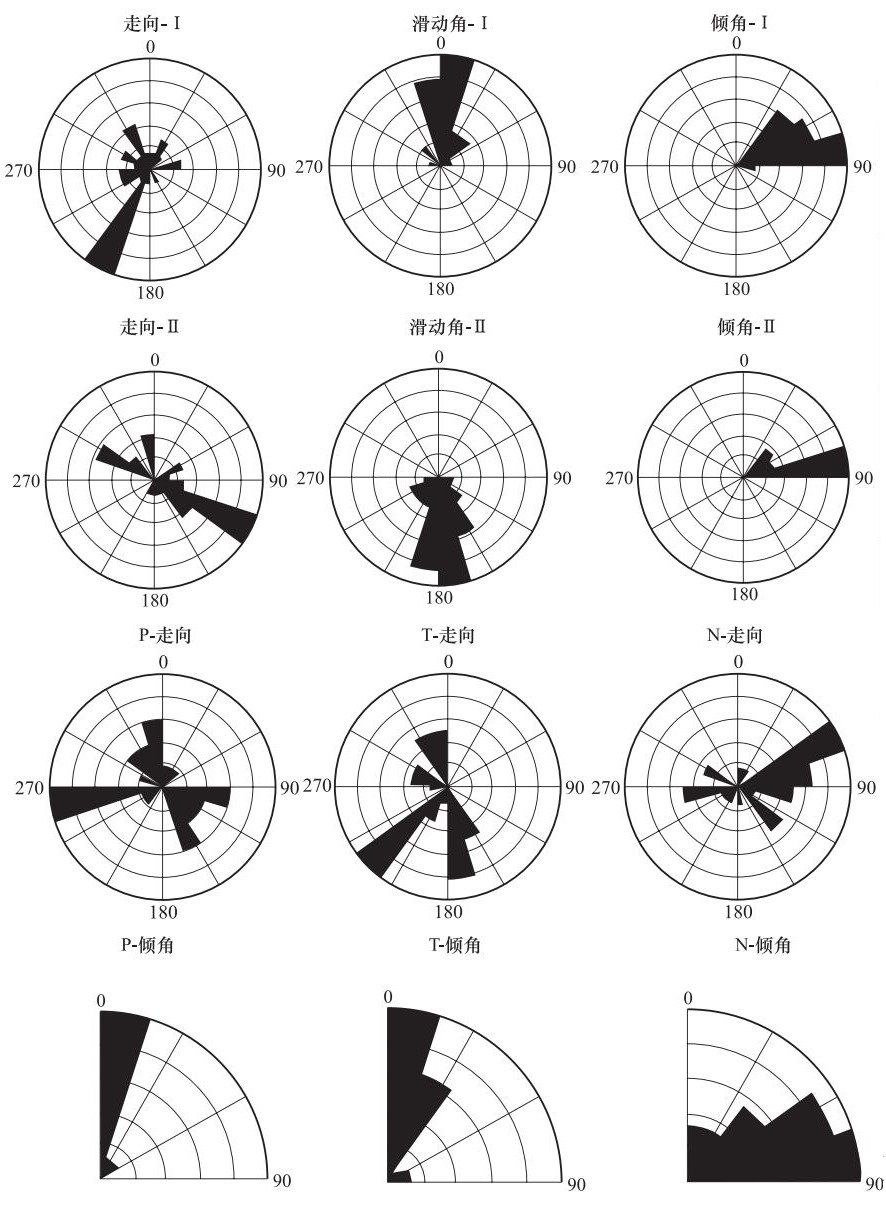
摘要: 2008年2—4月，位于汶川大震初始破裂点的紫坪铺水库附近发生了一系列的小震活动，它们与汶川地震和紫坪铺水库小震的关系值得研究。本文采用CAP方法，反演了紫坪铺水库7个专用数字地震台站的数据，得到震级大于ML 1.0的28个震源机制解。结果表明：有19个地震事件集中在紫坪铺水库东南方向的都江堰附近，最大地震为逆冲型，发震机制为逆冲型带走滑分量，少量带正断层分量；从深度剖面看，地震震源深度主要集中分布在地下13km附近区域，都江堰震群丛集在前山断裂带上，其它地震散布在中央断裂带上；发震最大主压应力方向随时间的变化具有从最大主压应力方向变化比较大到趋向一致的演化过程。这些现象说明龙门山断裂带在都江堰附近存在1个凸凹体，形成应力集中点，引发都江堰震群活动，由此迫使龙门山断裂带前山断裂发生逆冲性活动，从而加剧了龙门山断裂带中央断裂的活动，在一定程度上加速了汶川地震的发生。Abstract: A series of small earthquakes occurred in the vicinity of Zipingpu Reservoir at the beginning of the Wenchuan earthquake from February to April, 2008 and their relationship with the Wenchuan earthquake and the small earthquakes of the Zipingpu reservoir is worth studying. In this paper, the digital seismic data of seven special seismic stations of the Zipingpu reservoir are analyzed by using the CAP method, and 28 focal mechanisms with magnitude greater than ML1.0 level are obtained. The results show that 19 of these earthquakes are concentrated in the southeast of the Zipingpu Reservoir near Dujiangyan, in which the maximum earthquake is the thrust type, and the others are thrust with strike-slip and normal faulting. The focal depth of the earthquake is mainly distributed at the area above 13km depth, and the Dujiangyan earthquake swarm is concentrated in the front mountain fault zone, the other earthquakes are scattered on the central fault zone. In the change of the maximum main compressive stress direction over time, the change from the maximum main compressive stress direction is great and the trend is consistent. These evidences suggest that there is a convex and concave body in the Longmen mountain fault zone near Dujiangyan, which forms the stress concentration area. When the Dujiangyan earthquake swarm occurred to force the thrust of the Longmenshan fault, it intensified the activity of the central fault of the Longmenshan fault zone and accelerated the occurrence of the Wenchuan earthquake to some extent.
-
引言
众所周知，我国是地震频发的国家，地震可能造成高速铁路列车脱轨事故，为此，我国建立了相应的地震报警及紧急处置系统，力争在潜在破坏性地震到达之前发出报警，降低列车发生脱轨或倾覆的概率。目前广泛采用的地震报警参数主要为峰值加速度PGA，然而PGA主要体现地震波幅值，未考虑频谱及持时影响，对于无破坏性的高频小震可能产生误报现象。为避免这种干扰，郭恩栋等（2015）引入谱强度SI作为高速铁路地震报警参数，并给出相应的计算方法，SI从能量方面出发，考虑了幅值及频谱影响，忽略持时的影响，但相比PGA更合理。美国电力研究所EPRI（O'Hara 等，1991）在核电厂地震监测报警中引入累积绝对速度CAV作为报警参数，研究发现低频震动对CAV的贡献明显高于高频震动。我国三代核电站AP1000参考国外标准也引入了CAV作为地震报警参数（胡进军等，2013）。林宜娴（2002）提出CAV、PGA、PGV等参数可作为地震报警参数，其稳定性好，且确定性较高。Kostov（2005）根据欧洲几次强地震动数据，分析得出标准化累积绝对速度CAVSTD在预测地震动破坏能力方面明显优于PGA。伊斯坦布尔在地震预报警系统中利用累积绝对速度快速判别强地震动（Erdik等，2003）。Fahjan等（2011）在地震报警的触警算法中引入CAV，并提出新的用于报警系统的参数。黄俊等（2014）引入CAV作为报警参数，分析其在高速铁路报警中的适用性，研究发现CAV可有效排除破坏性小的高频小震对高速铁路列车地震报警的干扰。目前虽对CAV在地震报警中的应用有了深入研究，但在高速铁路列车地震报警中的研究较少，仅通过相关的地震波数据处理得出，未考虑车轨动力响应关系，且给出的计算参数为CAVSTD，为此，需探讨考虑车轨关系的基于相关起算阈值的CAV计算方法。
1. CAV相关参数
目前，地震工程界主要研究CAV、CAVSTD、CAV5。其中CAV于1988年由美国电力研究所（O'Hara等，1991）在核电厂报警中第2级判别标准中提出的，其概念为记录地震加速度数据的绝对值对记录时间进行积分，记为累积绝对速度CAV：
$${\rm{ CAV}} = \mathop \int \nolimits_0^{{{{t}}_{{\rm{max}}}}} \left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t$$ (1) 为提高CAV在核电厂报警中的准确度，EPRI在报告中引入标准化累积绝对速度CAVSTD，其可有效避免长持时记录的地震波尾部对应的幅值小且破坏性小的地震动对其数值的影响，其定义如下：将记录的加速度时程分成以1 s为时间间隔的N个小段，当1 s时间段内存在加速度绝对值≥0.025 g时，对该秒内加速度数值的绝对值进行积分，否则该秒内的积分值记为零，然后将整个记录时程进行相加求和，表达式为：
$$ {\rm{CA{V_{STD}}}} = \mathop \sum \limits_{{i=1}}^n \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\left| {{{a}}\left( {{t}} \right)} \right| < 0.025\;g}\\ {1,\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.025\;{{g}}} \end{array}} \right.$$ (2) Kramer等（2002）于2002年提出CAV5，用于场地液化判别，其概念为：将记录的加速度时程中对加速度数值的绝对值≥0.005 g进行积分求和，表达式为：
$${{\rm{ CAV}}_5} = \displaystyle\int \nolimits_0^\infty \left\langle {\rm{\chi }} \right\rangle \left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\left\langle {\rm{\chi }} \right\rangle = \left\{ {\begin{array}{*{20}{c}} {0\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.005\;g}\\ {1\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.005\;{{g}}} \end{array}} \right. $$ (3) 式中，a(t)为加速度时程，Wi为权重。
2. 改进的标准化累积绝对速度应用于高速铁路地震报警阈值中的计算方法
2.1 改进的标准化累积绝对速度起算阈值确定
本文引入31自由度的SY97477车辆模型（崔恩文，2014），结合车轨典型非线性接触关系，依据列车安全行驶的3项评判指标（脱轨系数、轮重减载率及横向力)，分析车体在轨道不平顺（我国高速铁路无砟轨道标准谱）与简谐波（仅考虑横向输入，与列车行驶方向垂直）共同激励下的动态响应，考虑95%的安全保证，引入2.55倍的动力放大系数（孙汉武等，2007），计算安全极限状态（超出3项指标任意1个限值）下不同车速对应的简谐波幅值随周期的变化关系，如图1所示。具体模型参数、车轨接触关系及评判标准可参考崔恩文（2014）的研究。
图 1 列车安全运行极限状态下不同车速对应的简谐波幅值随周期的变化关系Figure 1. The relationship between the amplitude of simple harmonic wave corresponding to different speeds and periods under the safe running limit state of the train由图1可知，车速一定时，即使幅值很小（<0.025 g）的低频简谐波也可能使列车脱轨，因此不能简单地套用标准化累积绝对速度CAVSTD计算公式，有必要研究改进的标准化累积绝对速度应用在高速铁路地震报警阈值中的计算方法。车速一定时，简谐波幅值随周期增加逐渐递减，最终趋于常数，且周期越大，不同车速对应的简谐波幅值之间的差值越小。车速为200 km/h时，当简谐波周期达2.2 s时，其幅值开始趋于常数，该常数约为0.008 g，本文规定此时的周期为简谐波幅值趋于常数对应的起始周期Tst，该常数记为Amin。不同车速下简谐波幅值趋于常数对应的起始周期及该常数的数值如表1所示。
表 1 不同车速下简谐波幅值趋于常数对应的起始周期及该常数的数值Table 1. The initial period of the simple harmonic wave amplitude tending to be constant at different speeds and the value of the constant项目 车速/（km·h−1） 200 250 300 350 400 起始周期Tst/s 2.2 2.3 2.1 2.0 1.7 Amin/g 0.008 0.004 0.004 0.004 0.004 由表1可知，车速为200 km/h与车速≥250 km/h时对应的Amin不同，车速≥250 km/h时Amin相同，但起始周期Tst随车速的增加呈递减趋势，说明车速越大，简谐波趋于常数所需的周期越小。
车速为200 km/h时，幅值低于0.008 g的简谐波对列车运行安全的影响可忽略不计。车速≥250 km/h时，幅值低于0.004 g的简谐波对列车运行安全的影响可忽略不计。由此可推算出改进的标准化累积绝对速度起算阈值，如表2所示。
表 2 不同车速下改进的标准化累积绝对速度起算阈值Table 2. Starting threshold of improved calculation of standardized cumulative absolute velocity at different speeds项目 车速/（km·h−1） 200 ≥250 改进的标准化累积绝对速度起算阈值/g 0.008 0.004 2.2 改进的标准化累积绝对速度应用在地震报警中的可行性分析
考虑改进的标准化累积绝对速度为累积过程的算法，其值对于加速度超过0.004 g或0.008 g的有限个数的高频小震会很小，因此，可较好地排除高速铁路沿线的高频小震，是较好的地震监测报警参数。
魏智祥（2015）分析了京武高速铁路线布置的强震仪监测到的列车运行时震动记录数据，发现列车运行产生的震动记录明显高于背景噪声，且发现东西、南北、垂直方向列车振动噪声幅值均≤0.002 g，由此可知本文设定的不同车速下改进的标准化累积绝对速度可有效排除列车振动的影响。
综上所述，本文给出改进的标准化累积绝对速度用于高速铁路地震报警是可行的。
2.3 改进的标准化累积绝对速度计算公式的确定
参照CAVSTD计算方法，本文给出车速为200 km/h时改进的标准化累积绝对速度CAV8计算公式如下：
$${{\rm{CAV}}_8} = \mathop \sum \limits_{i=1}^n \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.008\;g}\\ {1,\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.008\;{{g}}} \end{array}} \right.$$ (4) 当
$ a\left(t\right) $ $< 0.008\;g$ 时，${{W}}_{{i}}$ =0；当$\left|{a}\left({t}\right)\right|\geqslant 0.008\;g$ 时，${{W}}_{{i}}$ =1。本文给出的CAV8定义为：将加速度时程按1 s为时间间隔进行划分，如果在这1 s内加速度绝对值≥0.008 g，则对该秒内的加速度绝对值进行积分，否则忽略该秒内的积分值，然后将整个时程中每秒积分得到的数值进行累积求和。
车速为250 km/h时改进的标准化累积绝对速度CAV4计算公式如下：
$${ {\rm{CAV}}_4} = \mathop \sum \limits_{i=1}^{{n}} \mathop \int \nolimits_{{i}}^{{{i}} + 1} {W_i}\left| {{{a}}\left( {{t}} \right)} \right|{\rm{d}}t,\;\;\;\;\;{W_i} = \left\{ {\begin{array}{*{20}{c}} {0,\;\left| {{{a}}\left( {{t}} \right)} \right| < 0.004\;g}\\ {1,\;\left| {{{a}}\left( {{t}} \right)} \right| \geqslant 0.004\;{{g}}} \end{array}} \right.$$ (5) 当
${a}\left({t}\right)$ $< 0.004\;g$ 时，${{W}}_{{i}}=0$ ；当$\left|{a}\left({t}\right)\right|\geqslant 0.004\;{g}$ 时，${{W}}_{{i}}$ =1。本文给出的CAV4定义为：将加速度时程按1 s为时间间隔进行划分，如果在这1 s内加速度绝对值≥0.004 g，则对该秒内的加速度绝对值进行积分，否则忽略该秒内的积分值，然后将整个时程中每秒积分得到的数值进行累积求和。
3. 高速铁路地震报警阈值确定
为确定基于改进的标准化累积绝对速度高速铁路地震报警阈值，本文从Peer数据库选取6条不同场地地震波（表3），对应的加速度反应谱如图2所示，对其进行归一化处理，分析加速度幅值与评判列车脱轨3项指标之间的关系，确定不同车速下影响行车安全的6条地震波加速度上限值，按照本文给出不同车速下改进的标准化累积绝对速度计算公式，给出6条地震波对应的改进的标准化累积绝对速度上限值，如表4所示。
表 3 地震波相关信息Table 3. Seismic wave information项目 地震波台站名称 Cape Mendocino TCU045 Capitola Hector EL Centro Imp. Co. Cent Poe Road 震级 7.01 7.62 6.93 7.13 6.54 6.54 峰值加速度/g 0.376 5 0.008 1 0.528 5 0.265 6 0.357 9 0.446 3 v30/（m·s−1） 567.78 704.64 288.62 726.00 192.05 316.64 加速度记录持时/s 36.0 45.0 39.9 45.3 40.0 22.3 表 4 不同车速下6条地震波加速度上限值与改进的标准化累积绝对速度上限值Table 4. The upper limit of acceleration amplitudes and upper limit improved calculation of standardized cumulative absolute velocity CAV of six seismic waves at different speeds地震波台站名称 车速200 km/h 车速250 km/h 车速300 km/h 车速350 km/h 车速400 km/h 加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-sec加速度
上限值/
g改进的标准化
累积绝对速度
上限值/g-secCape Mendocino 0.074 0.17 0.070 0.17 0.055 0.13 0.040 0.09 0.039 0.09 TCU045 0.101 0.55 0.090 0.49 0.078 0.43 0.062 0.34 0.039 0.21 Capitola 0.109 0.34 0.078 0.25 0.062 0.20 0.054 0.17 0.039 0.11 Hector 0.101 0.27 0.070 0.19 0.062 0.17 0.054 0.14 0.047 0.12 EL Centro Imp. Co. Cent 0.078 0.16 0.070 0.18 0.054 0.13 0.039 0.08 0.027 0.05 Poe Road 0.074 0.19 0.054 0.14 0.043 0.11 0.039 0.10 0.035 0.08 由表4可知，车速相同时，即使地震波加速度相同，其对应的改进的标准化累积绝对速度不一定相同，如车速为200 km/h时，台站名称为Cape Mendocino与Poe Road的地震波加速度相同，但对应的改进的标准化累积绝对速度不同，且Cape Mendocino台站加速度记录持时较大，说明改进的标准化累积绝对速度与频谱紧密相关。车速≥250 km/h时，对于同一台站的地震波，峰值加速度越大其对应的改进的标准化累积绝对速度越大，如台站名称为Cape Mendocino的地震波，说明对于同一地震波而言，加速度影响累积绝对速度。根据改进的标准化累积绝对速度定义，加速度记录持时影响其数值。综上所述，改进的标准化累积绝对速度数值不仅与加速度幅值有关，还与频谱及加速度记录持时密切相关，可较好地反映地震动三要素。
选取6条地震波改进的标准化累积绝对速度最小值作为报警阈值，给出不同车速下基于改进的标准化累积绝对速度高速铁路地震报警阈值，如表5所示。由表5可知，改进的标准化累积绝对速度报警阈值与车速整体呈线性递减关系，中间车速对应的改进的标准化累积绝对速度可按线性插入计算。
表 5 不同车速下改进的标准化累积绝对速度高速铁路地震报警阈值Table 5. High-speed earthquake alarm threshold based on improved calculation of standardized cumulative absolute velocity thresholds at different vehicle speeds项目 车速/（km·h−1） 200 250 300 350 400 报警阈值/g-sec 0.16 0.14 0.11 0.08 0.05 4. 结论
（1）通过建立车轨模型，分析列车安全运行极限状态下简谐波幅值与周期的关系，得出不同车速下改进的标准化累积绝对速度起算阈值，并论证改进的标准化累积绝对速度在高速铁路地震报警中的可行性。
（2）参照标准化累积绝对速度CAVSTD计算公式，本文给出不同车速下改进的标准化累积绝对速度计算公式。
（3）根据本文给出的改进的标准化累积绝对速度计算公式，选取6条不同场地的地震波，分析列车在轨道不平顺及地震波共同激励下的动力响应，计算不同车速下改进的标准化累积绝对速度报警阈值，以供参考。
-
图 4 紫坪铺水库震源机制解平面分布图
Figure 4. The plane distribution of focal mechanism of the Zipingpu reservoir
图 5 紫坪铺水库震源机制解剖面分布图
Figure 5. The profile distribution of focal mechanism of the Zipingpu reservoir
图 6 节面Ⅰ、Ⅱ的走向、滑动角、倾角和P、T、N轴走向与倾角的统计特征
Figure 6. The strike, rake angle and dip angle of nodal planeIand Ⅱ, and the statistic characteristic of P, T, N axis and inclination
图 7 压应力轴（P轴）走向随时间变化图
Figure 7. Change of pressure stress axis (P-axis) trend with time
表 1 紫坪铺小台网基本情况
Table 1. The details of stations used in the study
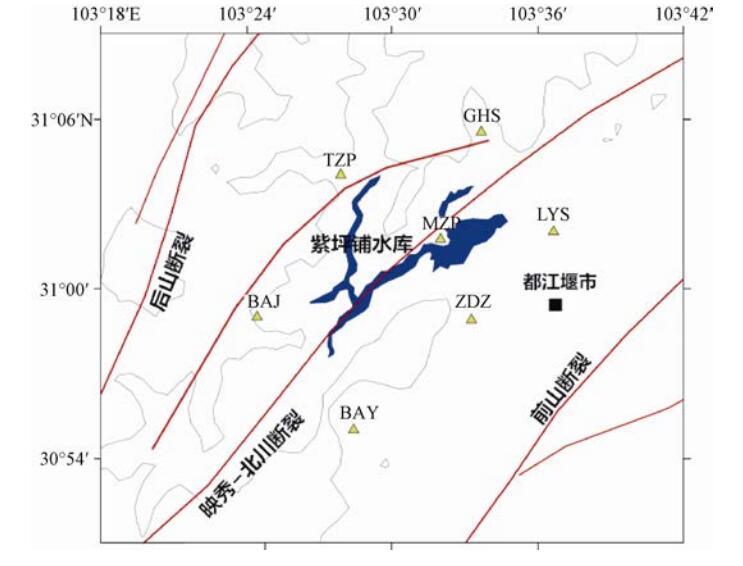
台站名称 台站代码 纬度/°N 经度/°E 八角台 BAJ 30.98 103.41 白岩台 BAY 30.92 103.47 桂花树台 GHS 31.09 103.56 灵岩寺台 LYS 31.03 103.61 庙子坪台 MZP 31.03 103.53 桃子坪台 TZP 31.07 103.46 钻洞子台 ZDZ 30.98 103.55 
下载: 导出CSV
表 2 研究区域一维速度模型
Table 2. Crustal velocity model in the study area
深度/km P波速度/km·s－1 S波速度/km·s－1 0 4.8 2.8 5 5.8 3.4 12 6.2 3.6 20 6.4 3.7 35 6.6 3.8
下载: 导出CSV
表 3 库区ML 1.0以上地震的震源机制参数
Table 3. The focal mechanism parameters of earthquakes with magnitude greater than ML 1.0 in the reservoir area
发震时间 发震地点 深度/km 震级/ML 节面Ⅰ 节面Ⅱ P轴 T轴 N轴 经度/°E 纬度/°N 走向
/°倾角
/°滑动角/° 走向
/°倾角
/°滑动角/° 走向
/°倾角
/°走向
/°倾角
/°走向
/°倾角
/°200802081609 103.603 30.977 11.4 1.13 191 61 －38 302 57 －145 155 46 247 2 339 44 200802100657 103.469 31.017 7.5 1.06 294 42 81 126 49 98 210 3 91 83 301 6 200802142134 103.654 30.945 13.3 1.849 355 49 －30 106 68 －135 329 47 226 11 126 41 200802142312 103.589 30.976 12.6 2.41 203 74 12 110 78 164 157 3 66 20 255 70 200802142336 103.598 30.981 12.8 1.397 204 80 19 111 71 169 336 6 68 20 231 69 200802142349 103.612 30.987 14.7 2.974 231 51 51 103 53 128 167 1 76 61 258 29 200802142350 103.597 30.978 13.2 2.958 36 85 －1 126 89 －175 351 4 261 3 138 85 200802150026 103.606 30.969 13.5 1.938 211 83 －1 301 89 －173 166 6 76 4 309 83 200802150043 103.611 30.971 13.5 1.303 214 66 22 115 70 154 165 3 73 32 259 58 200802150054 103.602 30.975 13.4 2.297 80 66 51 323 45 145 197 12 304 52 98 35 200802150615 103.605 30.977 13.1 1.03 5 58 －39 118 58 －141 331 49 62 0 152 41 200802150658 103.621 30.97 12.9 1.436 211 76 16 117 74 165 344 1 74 21 251 69 200802151624 103.602 30.968 13 1.201 33 90 1 303 89 180 168 1 258 1 32 89 200802151626 103.605 30.976 13.2 1.273 202 75 12 109 78 165 156 2 65 19 253 71 200802151637 103.608 30.969 13.4 1.145 35 78 1 305 89 168 351 8 259 9 120 78 200802181216 103.628 30.949 11.1 2.058 331 81 －14 63 76 －171 287 16 18 3 119 73 200802201131 103.615 30.965 13.2 2.125 339 66 －15 75 76 －155 299 27 206 7 102 62 200802201708 103.615 30.965 13.2 2.125 251 36 －1 342 89 －126 221 35 102 34 342 36 200802201824 103.374 30.92 2.8 1.246 251 36 －1 342 89 －126 221 35 102 34 342 36 200802212038 103.606 30.97 13.3 1.928 335 52 －79 137 39 －104 291 79 57 6 148 9 200802221649 103.432 30.956 3.8 1.001 268 84 －6 359 84 －174 223 8 133 0 43 82 200802270257 103.601 30.976 12.4 1.06 208 76 10 116 80 166 162 3 71 17 262 73 200803060843 103.461 31.08 9.6 1.055 146 90 2 56 88 180 281 1 11 1 147 88 200803062010 103.358 30.953 7.4 1.834 277 69 13 182 78 158 231 6 138 24 334 65 200803062028 103.536 30.919 16 1.205 81 55 50 317 51 133 198 2 292 58 107 32 200803081416 103.358 30.936 2.1 1.292 300 46 66 153 49 113 227 2 132 73 317 17 200804041034 103.43 30.967 9.4 1.228 261 75 2 170 88 165 217 9 125 12 343 75 200804131633 103.395 31.074 9.6 1.319 309 64 19 210 73 153 261 6 168 31 1 58
下载: 导出CSV
-
程建武, 董治平.2009.四川汶川8.0级地震前后中国大陆西部地震活动特征及震后趋势分析.华南地震, 29(4):54-63. http://www.cnki.com.cn/Article/CJFDTOTAL-HNDI200904009.htm 程万正, 张致伟, 阮祥, 2010.紫坪铺水库区不同蓄水阶段的地震活动及成因分析.地球物理学进展, 25(3):759-767. https://www.wenkuxiazai.com/doc/cdbd3290d0d233d4b14e6947.html 刁桂苓, 于利民, 李钦祖, 1994.强震前后震源区应力场变化一例.地震学报, 16(1):64-69. http://www.cnki.com.cn/Article/CJFDTOTAL-GYDZ200703001.htm 刁桂苓, 徐锡伟, 陈于高等, 2011.汶川MW 7.9和集集MW 7.6地震前应力场转换现象及其可能的前兆意义.地球物理学报, 2011, 54(1):128-136. 胡先明, 张永久, 谢蓉华等, 2009.紫坪铺水库区小地震震源机制研究.地震地质, 31(4):676-685. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_dzdz200904011 胡先明, 张炜, 韩进等, 2010.紫坪铺水库地震监测预测.四川地震, (4):1-6. http://mall.cnki.net/magazine/Article/SCHZ201004000.htm 李铂, 崔鑫, 苗庆杰等, 2016.CAP方法反演乳山震群3.0级以上地震震源机制解.华北地震科学, 34(3):14-19. http://mall.cnki.net/magazine/Article/HDKD201603003.htm 卢显, 张晓东, 周龙泉等, 2010.紫坪铺水库库区地震精定位研究及分析.地震, 30(2):10-19. http://mall.cnki.net/magazine/Article/DIZN201002002.htm 吕坚, 郑勇, 倪四道等, 2008.2005年11月26日九江-瑞昌MS 5.7、MS 4.8地震的震源机制解与发震构造研究.地球物理学报, 51(1):158-164. 马文涛, 徐长朋, 张新东等, 2011.紫坪铺水库与汶川地震关系的讨论.地震地质, 33(1):175-190. http://mall.cnki.net/magazine/Article/DZDZ201101019.htm 马瑾, 郭彦双, 2014.失稳前断层加速协同化的实验室证据和地震实例.地震地质, 36(3):547-561. http://www.cqvip.com/QK/95728X/201403/662620942.html 王椿镛, Mooney W. D., 王溪莉等, 2002.川滇地区地壳上地幔三维速度结构研究.地震学报, 24(1):1-16. http://www.cnki.com.cn/Article/CJFDTOTAL-DZXB200201000.htm 王卫民, 赵连峰, 李娟等, 2008.四川汶川8.0级地震震源过程.地球物理学报, 51(5):1403-1410. http://mall.cnki.net/magazine/Article/DQWX200805014.htm 徐锡伟, 闻学泽, 叶建青等, 2008.汶川MS 8.0地震地表破裂带及其发震构造.地震地质, 30(3):597-629. doi: 10.1007/s11430-015-5170-y-44?slug=full%20text 易桂喜, 闻学泽, 辛华等, 2013.龙门山断裂带南段应力状态与强震危险性研究.地球物理学报, 56(4):1112-1120. doi: 10.6038/cjg20130407 张培震, 徐锡伟, 闻学泽等, 2008.2008年汶川8.0级地震发震断裂的滑动速率、复发周期和构造成因.地球物理学报, 51(4):1066-1073. http://www.cnki.com.cn/Article/CJFDTOTAL-DQWX200804017.htm 张永久, 高原, 石玉涛等, 2010.四川紫坪铺水库库区地震剪切波分裂研究.地球物理学报, 53(9):2091-2101. http://manu39.magtech.com.cn/Geophy/CN/abstract/abstract3307.shtml 郑培玲, 邢康, 贾漯昭等, 2017.2015年1月18日河南范县ML 4.2地震震源机制解分析.地震地磁观测与研究, 38(1):28-31. 周龙泉, 2009.紫坪铺水库库区三维速度结构.国际地震动态, (4):5-6. http://mall.cnki.net/magazine/Article/GJZT200904007.htm Zhao L. S., Helmberger D. V., 1994. Source estimation from broadband regional seismograms. Bulletin of the Seismological Society of America, 84(1):91-104. Zhu L. P., Rivera L. A., 2002. A note on the dynamic and static displacements from a point source in multilayered media. Geophysical Journal International, 148(3):619-627. -
下载:
点击查看大图
计量
- 文章访问数: 110
- HTML全文浏览量: 17
- PDF下载量: 4
- 被引次数: 0
