Shaking Table Test of Steel-asphalt Isolation Layer and Its Seismic Response Analysis in Masonry Structure Electric Power House with Different Heights
-
摘要: 为弥补试验的不足,对试验室里难以实现的情况进行研究,如大比例甚至足尺模型的动力试验,利用大型有限元软件MSC.MARC对钢筋-沥青复合隔震层建立了非线性有限元模型。利用钢筋非线性子程序UBEAM和非线性弹簧子程序USPRNG,分别模拟了钢筋和砖墩-上梁之间相互作用关系的非线性情况,引入了沥青油膏的温度影响系数。为验证该模型,在钢筋沥青隔震层试件振动台试验的基础上,对振动台试验中各试件的模态进行了计算、对各工况进行了三维有限元时程分析,并将分析结果与试验结果对比,计算结果与试验结果吻合较好,验证了该模型的准确性和合理性。最后利用该模型,建立了不同高度的砌体结构有限元模型,设计并建立了相应的墙下条形隔震层模型,对钢筋沥青复合隔震层在不同高度的砌体结构中的动力性能和隔震效果进行了数值模拟,并对计算结果进行了归纳和分析,得出了一系列有用的结论。Abstract: To remedy defects of tests in laboratory, study more situations which are difficult to achieve in it, such as large-scale even the full scale dynamic testing. In this paper a non-linear finite element model of steel-asphalt isolation layer was established through finite element software MSC.MARC. By using steel non-linear subroutine UBEAM and spring nonlinear subroutine USPRNG, the non-linearity of steel and the nonlinear interaction between brick pier and upper beam were respectively simulated. The temperature factor of asphalt ointment was also proposed. To verify the model, on the basis of shaking table test of steel-asphalt isolation layer, modes of specimens in shaking table tests were calculated, and all conditions in the shaking table tests were simulated by 3D Finite Element time history analysis. Comparison of the calculated results with the experimental results shows good agreement, which verifies the accuracy and reasonableness of the model. Finally, our models were set up in finite element models with different masonry structures in different heights, and the corresponding isolation layer models under strip foundation were design and built. The dynamic performance and isolation effect of the steel-asphalt isolation layer in different masonry structures with different heights of was simulated, and a series of useful conclusions were drawn.
-
Key words:
- Seismic isolation /
- Steel-asphalt isolation layer /
- Shaking table test /
- Finite element /
- Nonlinear
-
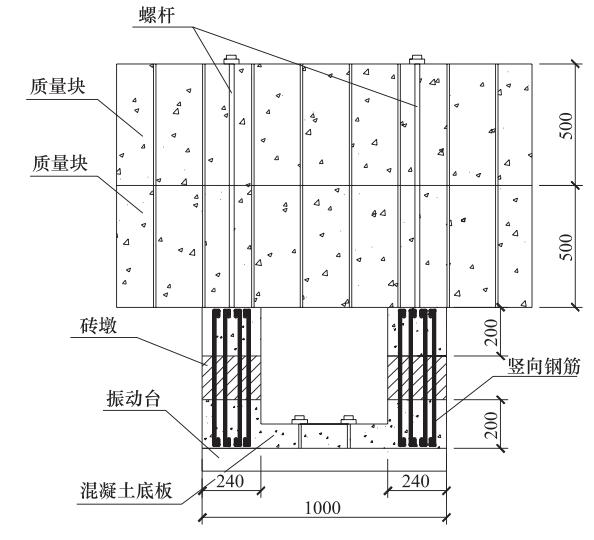
表 1 隔震层试件参数
Table 1. Parameters of isolation layer specimen
试件编号 隔震层高度/mm 竖向钢筋配置 混凝土强度 砖强度 砂浆强度 有无沥青 GZC200-6-1 200 40C6 C30 Mu10 M5 有 GZC300-6-1 300 40C6 C30 Mu10 M5 有 GZC200-6-2 200 40C6 C30 Mu10 M10 无 GZC200-8-2 200 20C8 C30 Mu10 M10 无 注:以GZC200-6-1为例,试件编号中“GZC200”表示隔震层高度为200mm,“6”表示钢筋直径为6mm,“1”表示砖墩之间填充有防锈沥青油膏;“2”表示砖墩之间没有填充沥青油膏,“1”和“2”在砖墩上方都有一层沥青油膏作为垫层。 表 2 加速度与相对位移最大值汇总表
Table 2. Maximum acceleration and relative displacement
工况代号 输入加速度幅值绝对值/m·s-2 输出加速度幅值绝对值/m·s-2 加速度幅值比β 隔震层最大水平相对位移绝对值/mm 200-6-1El0.1 0.96 0.48 0.50 2.6 200-6-1El0.2 1.98 0.92 0.46 7.8 200-6-1El0.3 3.14 1.32 0.42 8.5 200-6-1El0.4 4.32 1.83 0.42 10.9 200-6-1Taft0.1 1.29 0.68 0.53 2.7 200-6-1Taft0.2 2.18 1.38 0.63 9.1 200-6-1Taft0.3 3.13 1.40 0.45 9.8 200-6-1Taft0.4 4.14 1.64 0.40 10.9 300-6-1El0.1 1.16 0.56 0.48 2.5 300-6-1El0.2 2.17 0.89 0.41 7.6 300-6-1El0.3 3.17 1.24 0.39 8.6 300-6-1Taft0.1 1.04 0.69 0.66 2.7 300-6-1Taft0.2 2.13 1.04 0.49 8.2 300-6-1Taft0.3 3.10 1.30 0.42 10.1 200-6-2El0.1 0.83 0.55 0.66 2.2 200-6-2El0.2 1.66 1.14 0.69 4.8 200-6-2El0.3 3.28 2.09 0.64 7.6 200-6-2El0.4 4.28 2.62 0.61 9.2 200-6-2El0.5 5.42 3.08 0.57 13.6 200-6-2El1.0 10.35 5.69 0.55 19.8 200-6-2El1.7 17.13 8.22 0.48 29.7 200-6-2Taft0.1 1.27 0.92 0.72 3.2 200-6-2Taft0.2 1.95 1.50 0.77 5.6 200-6-2Taft0.3 2.83 2.09 0.74 7.6 200-6-2Taft0.4 3.83 2.66 0.69 9.3 200-6-2Taft0.5 6.41 4.58 0.71 14.2 200-6-2Taft1.1 11.83 7.22 0.61 16.5 200-6-2Taft1.7 17.11 8.27 0.48 24.3 200-8-2El0.1 0.72 0.61 0.85 1.7 200-8-2El0.2 2.39 1.53 0.64 4.5 200-8-2El0.3 3.40 2.37 0.70 7.2 200-8-2El0.5 5.03 3.67 0.73 10.2 200-8-2El0.6 5.48 3.91 0.71 15.4 200-8-2El1.7 17.0 11.9 0.70 36.1 200-8-2Taft0.1 1.60 1.51 0.94 2.6 200-8-2Taft0.2 2.22 1.78 0.80 3.5 200-8-2Taft0.3 3.35 1.86 0.55 4.9 200-8-2Taft0.4 4.37 2.81 0.64 6.2 200-8-2Taft0.6 6.99 4.22 0.60 14.1 200-8-2Taft1.5 15.12 5.66 0.37 29.3 注:加速度幅值比β=隔震层顶部加速度幅值/隔震层底部加速度幅值。 表 3 试验与计算结果对比表
Table 3. Comparison of test and calculated results
工况代号 试验所得加速度幅值比β 计算所得加速度幅值比β′ 误差百分比/% 200-6-1El0.1 0.50 0.46 8.0 200-6-1El0.2 0.46 0.45 2.2 200-6-1El0.3 0.42 0.44 4.8 200-6-1El0.4 0.42 0.43 2.4 200-6-1Taft0.1 0.53 0.54 1.8 200-6-1Taft0.2 0.63 0.53 15.8 200-6-1Taft0.3 0.45 0.48 6.7 200-6-1Taft0.4 0.40 0.38 5.0 300-6-1El0.1 0.48 0.44 8.3 300-6-1El0.2 0.41 0.41 0.0 300-6-1El0.3 0.39 0.38 2.5 300-6-1Taft0.1 0.66 0.54 18.1 300-6-1Taft0.2 0.49 0.51 4.1 300-6-1Taft0.3 0.42 0.46 9.5 200-6-2El0.1 0.66 0.71 7.6 200-6-2El0.2 0.69 0.70 1.4 200-6-2El0.3 0.64 0.70 9.4 200-6-2El0.4 0.61 0.65 6.6 200-6-2El0.5 0.57 0.60 5.3 200-6-2El1.0 0.55 0.55 0.0 200-6-2El1.7 0.48 0.52 8.3 200-6-2Taft0.1 0.72 0.81 12.5 200-6-2Taft0.2 0.77 0.79 2.7 200-6-2Taft0.3 0.74 0.74 0.0 200-6-2Taft0.4 0.69 0.61 11.6 200-6-2Taft0.5 0.71 0.61 14.1 200-6-2Taft1.1 0.61 0.58 4.9 200-6-2Taft1.7 0.48 0.47 2.1 200-8-2El0.1 0.85 0.79 7.1 200-8-2El0.2 0.64 0.75 17.2 200-8-2El0.3 0.70 0.72 2.9 200-8-2El0.5 0.73 0.71 2.7 200-8-2El0.6 0.71 0.69 2.8 200-8-2El1.7 0.70 0.67 4.3 200-8-2Taft0.1 0.94 0.88 6.4 200-8-2Taft0.2 0.80 0.84 5.0 200-8-2Taft0.3 0.55 0.70 27.3 200-8-2Taft0.4 0.64 0.67 4.7 200-8-2Taft0.6 0.60 0.61 1.7 200-8-2Taft1.5 0.37 0.41 8.1 表 4 各试件隔震层参数设计
Table 4. Parameter design of isolation layer for all specimens
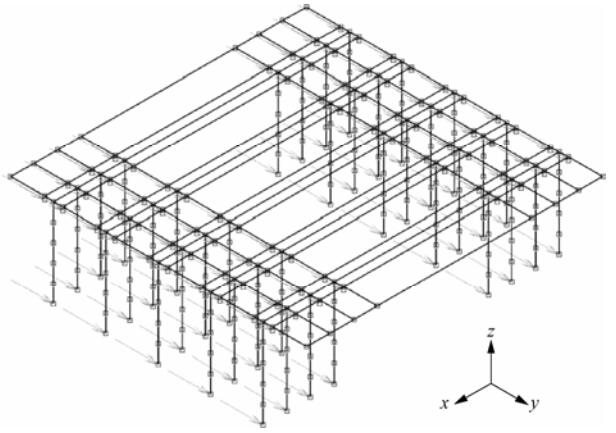
试件号 分布位置 钢筋直径/mm 钢筋数/根·m-1 隔震层高度/mm Q1 外墙下 6 15 300 内墙下 6 20 Q3 外墙下 8 20 400 内墙下 10 20 Q5 外墙下 10 20 400 内墙下 12 20 Q7 外墙下 12 20 400 内墙下 14 20 注:试件号“Q1”表示一层的砌体结构,其余相同。4个试件的上部结构只是层数不同,跨度、跨数、面积等其余参数均相同,隔震层竖向钢筋等级均为HRB400。 表 5 计算工况表
Table 5. Calculation table of working condition
试件号 输入波形 输入峰值加速度/g 隔震结构工况代号 非隔震结构工况代号 Q1 El-Centro 0.1 Q1El0.1-G Q1El0.1 0.3 Q1El0.3-G Q1El0.3 1.0 Q1El1.0-G Q1El1.0 Taft 0.1 Q1Taft0.1-G Q1Taft0.1 0.3 Q1Taft0.3-G Q1Taft0.3 1.0 Q1Taft1.0-G Q1Taft1.0 Q3 El-Centro 0.1 Q3El0.1-G Q3El0.1 0.3 Q3El0.3-G Q3El0.3 1.0 Q3El1.0-G Q3El1.0 Taft 0.1 Q3Taft0.1-G Q3Taft0.1 0.3 Q3Taft0.3-G Q3Taft0.3 1.0 Q3Taft1.0-G Q3Taft1.0 Q5 El-Centro 0.1 Q5El0.1-G Q5El0.1 0.3 Q5El0.3-G Q5El0.3 1.0 Q5El1.0-G Q5El1.0 Taft 0.1 Q5Taft0.1-G Q5Taft0.1 0.3 Q5Taft0.3-G Q5Taft0.3 1.0 Q5Taft1.0-G Q5Taft1.0 Q7 El-Centro 0.1 Q7El0.1-G Q7El0.1 0.3 Q7El0.3-G Q7El0.3 1.0 Q7El1.0-G Q7El1.0 Taft 0.1 Q7Taft0.1-G Q7Taft0.1 0.3 Q7Taft0.3-G Q7Taft0.3 1.0 Q7Taft1.0-G Q7Taft1.0 表 6 各砌体模型在不同工况下的基频比较
Table 6. Comparison of fundamental frequencies of seperately masonry models under different working conditions
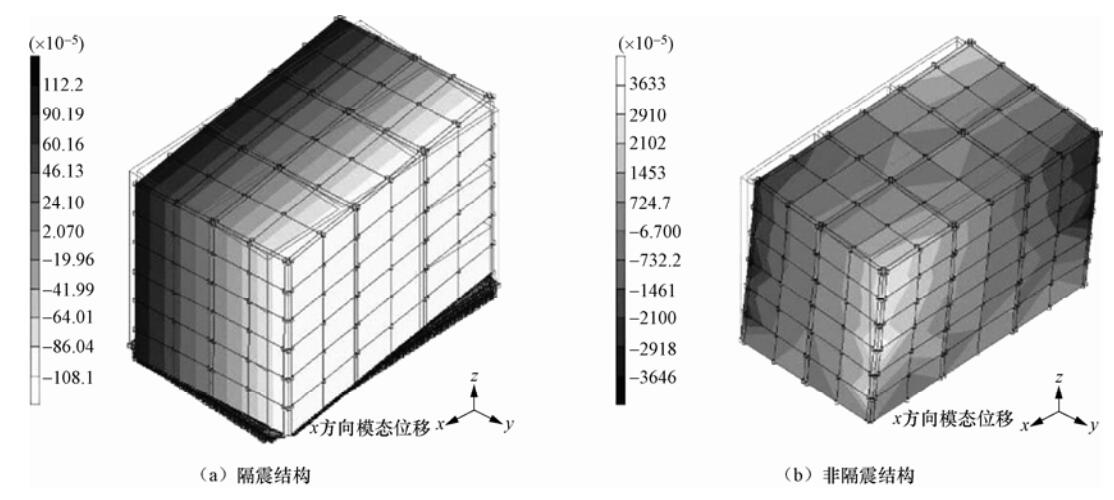
试件号 一阶自振频率/Hz 隔震结构 非隔震结构 Q1 1.043 21.20 Q3 0.920 6.444 Q5 1.067 3.278 Q7 1.079 1.973 表 7 砌体结构各工况加速度幅值比汇总表
Table 7. Acceleration amplitude ratio of masonry structure under different working conditions
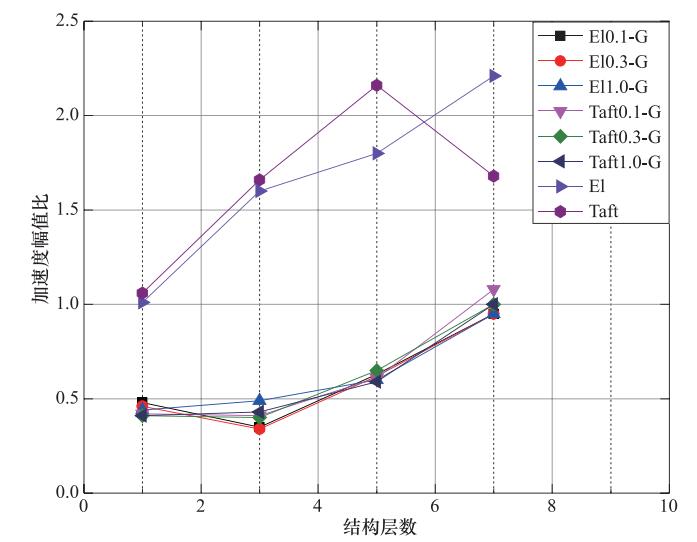
工况代号 加速度幅值比 隔震结构β1 非隔震结构β2 Q1El0.1(-G) 0.48 1.01 Q1El0.3(-G) 0.46 1.01 Q1El1.0(-G) 0.44 1.01 Q1Taft0.1(-G) 0.42 1.06 Q1Taft0.3(-G) 0.41 1.06 Q1Taft1.0(-G) 0.41 1.06 Q3El0.1(-G) 0.35 1.60 Q3El0.3(-G) 0.34 1.60 Q3El1.0(-G) 0.49 1.60 Q3Taft0.1(-G) 0.41 1.66 Q3Taft0.3(-G) 0.40 1.66 Q3Taft1.0(-G) 0.43 1.66 Q5El0.1(-G) 0.63 1.80 Q5El0.3(-G) 0.62 1.80 Q5El1.0(-G) 0.60 1.80 Q5Taft0.1(-G) 0.61 2.16 Q5Taft0.3(-G) 0.65 2.16 Q5Taft1.0(-G) 0.59 2.16 Q7El0.1(-G) 0.95 2.21 Q7El0.3(-G) 0.95 2.21 Q7El1.0(-G) 0.95 2.21 Q7Taft0.1(-G) 1.08 1.68 Q7Taft0.3(-G) 1.00 1.68 Q7Taft1.0(-G) 1.00 1.68 -
韩淼, 王秀梅, 2004.基础隔震技术的研究现状.北京建筑工程学院学报, 20(2):11-14. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=bjjzgcxyxb200402003 李书进, 毛羚, 陶礼龙等, 2010.湖北农村民居抗震性能调查与分析.震灾防御技术, 5(1):116-124. doi: 10.11899/zzfy20100114 陆鸣, 田学民, 王笃国等, 2006.建筑结构基础隔震技术的研究和应用.震灾防御技术, 1(1):31-38. doi: 10.11899/zzfy20060105 尚守平, 郜志远, 徐梅芳, 2011.新型隔震墩在农村民居中的应用.施工技术, 40(6):58-61. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sgjs201106017 尚守平, 黄群堂, 沈戎等, 2012.钢筋-沥青隔震墩砌体结构足尺模型试验研究.建筑结构学报, 33(3):132-139. http://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201203023.htm 杨林, 常永平, 周锡元等, 2008.FPS隔震体系振动台试验与有限元模型对比分析.建筑结构学报, 29(4):66-72. http://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201404027.htm 杨钦杰, 刘华贵, 高鹏飞等, 2016.广西农村民居抗震性能调查研究.震灾防御技术, 11(1):100-110. doi: 10.11899/zzfy20160111 郑瑶, 侍雪雷, 王毅红等, 2016.村镇隔震砌体结构振动台试验方案设计研究.震灾防御技术, 11(2):297-305. doi: 10.11899/zzfy20160212 Ashkezaria G. D., Aghakouchaka A. A., Kokabi M., 2008. Design, manufacturing and evaluation of the performance of steel like fiberreinforced elastomeric seismic isolators. Journal of Material Processing Technology, 197(1-3):140-150. doi: 10.1016/j.jmatprotec.2007.06.023 Lu L. Y., Chung L. L., Wu L. Y., et al., 2006. Dynamic analysis of structures with friction devices using discrete-time state-space formulation. Computers & Structures, 84(15-16):1049-1071. https://www.deepdyve.com/lp/elsevier/dynamic-analysis-of-structures-with-friction-devices-using-discrete-rwPAiQViTW Matsagar V. A., Jangid R. S., 2003. Seismic response of base-isolated structures during impact with adjacent structures. Engineering Structures, 25(10):1311-1323. doi: 10.1016/S0141-0296(03)00081-6 Naeim F., Kelly J. M., 1999. Design ofseismic isolated structures:from theory to practice. New York:John Wiley and Sons Inc., 123-142. Shakib H., Fuladgar A., 2003. Response of pure-friction sliding structures to three components of earthquake excitation. Computers & Structures, 81(4):189-196. https://www.researchgate.net/publication/265352007_Response_of_Pure-Friction_Sliding_Structures_to_Three_Components_of_Earthquake_Excitation_Considering_Variations_in_the_Coeecient_of_Friction -




 下载:
下载: