The Application of Ultra Shallow Seismic Survey on Wanggezhuang Fault in Qingdao
-
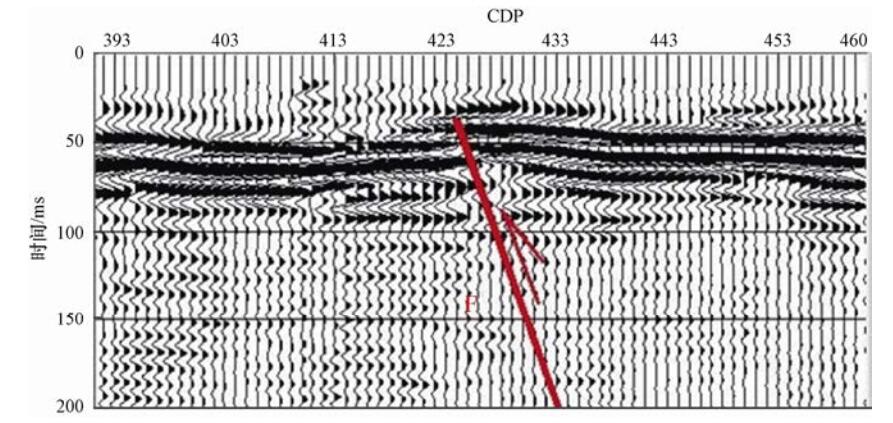
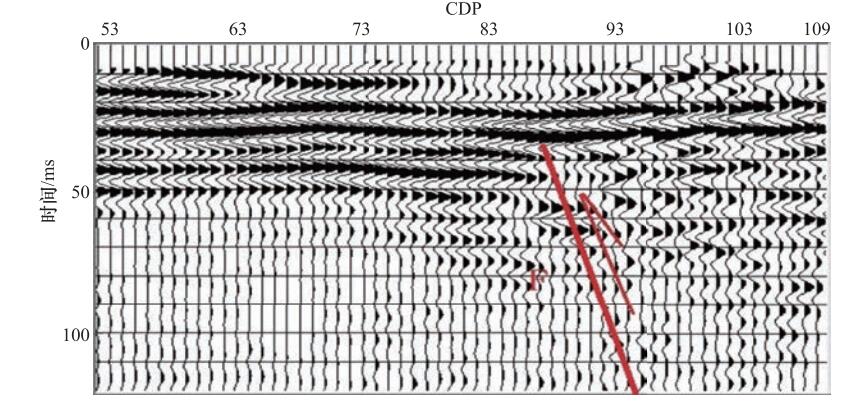
摘要: 目前国内外对目标层埋深仅有几十米（甚至十几米）的超浅层地震勘探经验不多，理论研究也不够深入。本文从城市活断层探测的角度出发，利用地质学、地球物理学及数学等学科中的相关理论和方法，探讨超浅层地震勘探在青岛复杂地质构造背景下取得有效探测结果的前提条件，并对青岛市主要活断层的典型剖面进行重点研究，力求在城市活断层超浅层地震勘探数据采集技术、数据处理等方面有所进展，为青岛及类似地质构造背景的地区开展活动断层超浅层地震探测提供参考。研究表明超浅层地震反射波法可以获取深度仅有十几米的地层反射信号，且大部分反射剖面都可较清楚地揭示出超浅部断层位置和断层特征。Abstract: At present for the target at depth of only tens of meters of ultra-shallow seismic exploration do not have many experiences in practice neither in theoretical research. The depth about decades of meters below the ground surface is the blind area of every kind of deep and shallow seismic exploration, which plays an important role in the research of the location of fault and active structure. Starting from the point of view of detecting urban active faults, we apply related theories and methods of geology and geophysics, probe into the precondition to acquire efficient ultra-shallow seismic results in complicated geological background. Taking the Qingdao area as an example, we study the depth condition of Quaternary deposits, and apply 4-8 stacking folds to satisfy the requirement to get the exploration results with high-resolution and high-SNR. Preliminary results reveal that the selecting proper surveillance layout is one of the keys to acquire authentic exploration results in ultra-shallow P-wave reflection exploration. Our results also show that ultra-shallow seismic reflection method in detecting faults in the Qingdao area has good application prospects.
-
Key words:
- Ultra shallow seismic survey /
- Observation system /
- Wang G Z Fault /
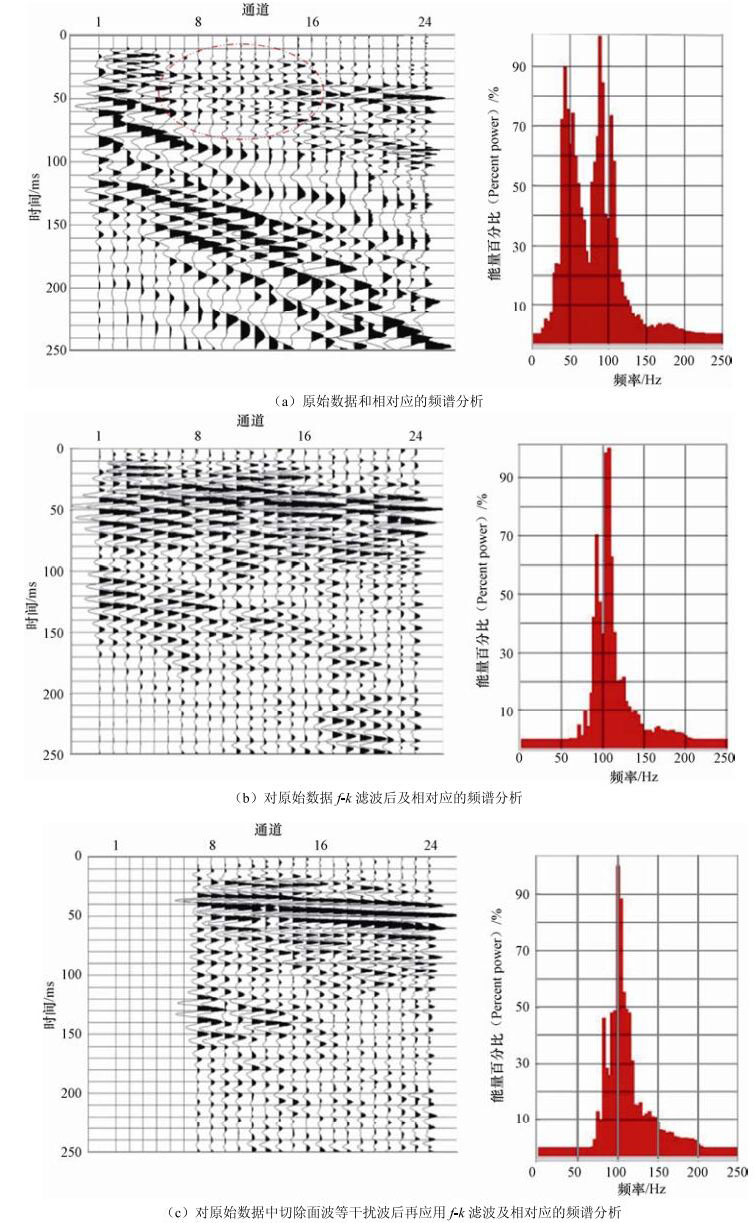
- f-k filtering
-
引言
关于场地地震反应的分析已有大量研究成果，研究表明土壤在地震作用下会表现出材料非线性效应ADDIN EN.CITE.DATA（Joyner等，1975；Huang等，2001；Arslan等，2006；Hosseini等，2012）。等效线性化方法ADDIN EN.CITE.DATA（Schnabel等，1972；Idriss等，1992；Bardet等，2000；王笃国等，2016）是一种频域方法，通过在不同土体应变条件下选择等效阻尼比和剪切模量，将非线性问题转化为线性问题。当采用材料非线性本构模型描述土体非线性时，需采用时间积分算法求解非线性动力有限元方程。时间积分算法可分为隐式方法和显式方法。隐式算法每时刻需求解线性代数方程组，计算效率相对较低，如Wilson-θ法和Newmark法等。显式算法无需求解线性代数方程组，适合于强非线性和自由度数目较大的问题。研究者已提出多种显式时间积分算法ADDIN EN.CITE.DATA（Chung等，1994；王进廷等，2002；Belytschko等，2014）。作者近期提出一种二阶精度的单步显式算法，该算法适合变时步问题，在线弹性范围内稳定性较好。本文将该算法推广至求解非线性动力有限元方程中，并将其应用于地震波垂直入射时非线性地震反应分析。
1. 非线性动力有限元方程的显式时间积分算法
设已知非线性体系第${t_i}$时步的受力状态，求解第${t_{i + 1}}$时步的非线性结构动力学方程：
$${\boldsymbol{M}}{{\boldsymbol{\ddot u}}_{i + 1}}{\boldsymbol{ + C}}{{\boldsymbol{\dot u}}_{i + 1}} + {\boldsymbol{f}}_{i + 1}^S{\boldsymbol{ = }}{{\boldsymbol{f}}_{i + 1}}$$ (1) 式中M、C、${{\boldsymbol{f}}^S}$和${\boldsymbol{f}}$分别表示非线性体系的质量矩阵、阻尼矩阵、内力向量和外荷载向量；u表示位移，点号对时间t求导，i+1表示第${t_{i + 1}}$时刻。第i+1时刻时间步长为：
$${\boldsymbol{\Delta }}{t_i} = {t_{i + 1}} - {t_i}$$ (2) 文献显式方法求解非线性方程（1）的过程如下，第i+1时刻位移${{\boldsymbol{u}}_{i + 1}}$为：
$${{\boldsymbol{u}}_{i + 1}} = {{\boldsymbol{u}}_i} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{t_i}{{\boldsymbol{\dot u}}_i} + \frac{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{t_i}^2}}{2}{{\boldsymbol{\ddot u}}_i}$$ (3) 第i+1时刻位移增量$\mathit{\Delta }{{\boldsymbol{u}}_i}$、内力增量$\mathit{\Delta }{\boldsymbol{f}}_i^S$和内力全量${\boldsymbol{f}}_{i + 1}^S$分别为：
$$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\boldsymbol{u}}_i} = {{\boldsymbol{u}}_{i + 1}} - {{\boldsymbol{u}}_i}$$ (4) $$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{f}}_i^S = {\boldsymbol{f}}(\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\boldsymbol{u}}_i})$$ (5) $${\boldsymbol{f}}_{i + 1}^S = {\boldsymbol{f}}_i^S + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{f}}_i^S$$ (6) 第i+1时刻预估速度${{\boldsymbol{\dot {\tilde u}}}_{i + 1}}$、预估加速度${{\boldsymbol{\ddot {\tilde u}}}_{i + 1}}$、速度${{\boldsymbol{\dot u}}_{i + 1}}$和加速度${{\boldsymbol{\ddot u}}_{i + 1}}$分别为
$${{\boldsymbol{\dot {\tilde u}}}_{i + 1}} = {{\boldsymbol{\dot u}}_i} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{t_i}{{\boldsymbol{\ddot u}}_i}$$ (7) $${{\boldsymbol{\ddot {\tilde u}}}_{i + 1}} = {{\boldsymbol{M}}^{ - 1}}({{\boldsymbol{f}}_{i + 1}} - {\boldsymbol{C\dot {\tilde u}}}_{i + 1}^{} - {\boldsymbol{f}}_{i + 1}^S)$$ (8) $${{\boldsymbol{\dot u}}_{i + 1}} = {{\boldsymbol{\dot u}}_i} + \frac{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{t_i}}}{2}({{\boldsymbol{\ddot u}}_i} + {{\boldsymbol{\ddot {\tilde u}}}_{i + 1}})$$ (9) $${{\boldsymbol{\ddot u}}_{i + 1}} = {{\boldsymbol{M}}^{ - 1}}({{\boldsymbol{f}}_{i + 1}} - {\boldsymbol{C\dot u}}_{i + 1}^{} - {\boldsymbol{f}}_{i + 1}^S)$$ (10) 式（3）—式（10）为求解式（1）的显式算法。算法中需由位移增量计算内力增量，目前常用的应力计算方法包括向前欧拉法、向后欧拉法和完全隐式计算法等ADDIN EN.CITE.DATA（Sloan等，1992；2001；Ahadi等，2003）。下面给出式（5）由位移增量计算内力增量的过程，即一种带误差控制的修正欧拉算法。
对于每个有限单元，由位移增量$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{u}}_i^e$计算应变增量$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e$的表达式为：
$$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e = {{\boldsymbol{B}}^e}\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{u}}_i^e$$ (11) 式中Be为应变矩阵。将ti时刻单元应变增量$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e$赋值给子步应变增量$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e$，ti时刻单元应力${\boldsymbol{ \pmb{\mathit{ σ}} }}_i^e$赋值给${\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e$，初始化子步应变增量和应力状态分别为：
$$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e \leftarrow \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e$$ (12) $${\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e \leftarrow {\boldsymbol{ \pmb{\mathit{ σ}} }}_i^e$$ (13) 每个子步中应力增量计算思路见图 1，具体计算公式如下：
$${\boldsymbol{D}}_1^e = {\boldsymbol{D}}({\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e)$$ (14) $$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_1^e = {\boldsymbol{D}}_1^e\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e$$ (15) $${\boldsymbol{D}}_2^e = {\boldsymbol{D}}({\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_1^e)$$ (16) $$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_2^e = {\boldsymbol{D}}_2^e\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e$$ (17) $$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_s^e = \frac{{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_1^e + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_2^e}}{2}$$ (18) 式中${{\boldsymbol{D}}^e}$为单元应力-应变关系矩阵。判断每个子步中应力增量$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{{\boldsymbol{ \pmb{\mathit{ σ}} }}_s}$是否符合精度要求的误差判断式为：
$${e_r} = \frac{{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_1^e - \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_2^e} \right\|}}{{\left\| {{\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_s^e} \right\|}}$$ (19) 判断误差er是否小于预先给定的判断值st，条件不满足时，缩小子步应变增量为：
$$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e \leftarrow A\sqrt {{{{s_t}} \mathord{\left/ {\vphantom {{{s_t}} {{e_r}}}} \right. } {{e_r}}}} \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e$$ (20) 式中A为误差峰值系数。采用缩小的子步应变增量重新进行式（14）—式（19）的计算与判断，循环直至满足精度要求，更新剩余应变增量和应力状态分别为：
$$\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e \leftarrow \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_i^e - \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ ε}} }}_s^e$$ (21) $${\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e \leftarrow {\boldsymbol{ \pmb{\mathit{ σ}} }}_{i + 1}^e + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\boldsymbol{ \pmb{\mathit{ σ}} }}_s^e$$ (22) 利用更新剩余应变增量和应力状态循环执行式（14）—式（20），直至剩余应变增量小于等于零结束。
利用求得的第i+1时刻单元应力可得到单元应力增量和内力增量分别为：
$$ \Delta \boldsymbol{\sigma }_i^e = \boldsymbol{\sigma }_{i + 1}^e - \boldsymbol{\sigma }_i^e $$ (23) $$ \Delta {\boldsymbol{f}}_i^S{\rm{ = }}\sum\limits_e {\int {{{\boldsymbol{B}}^{e{\rm{T}}}}\boldsymbol{\Delta }{\boldsymbol{\sigma }}_i^e{\bf{d}}A} } $$ (24) 2. 地震波垂直入射时场地非线性地震反应分析
本节将上述非线性有限元方程的显式时间积分算法应用于地震波垂直入射时场地非线性地震反应分析中。假定基岩为线弹性半空间，考虑基岩上覆土层的材料非线性，不考虑土体阻尼。在土层下部设置黏性边界条件模拟半空间基岩的辐射阻尼，并在该处以等效结点力的方式实现地震动输入。
计算模型见图 2，选取A点作为观测点。土体非线性材料本构模型选取邓肯-张模型，土体线弹性参数见表 1，未给出配套的非线性参数，故算例中的非线性参数参考实际情况选取，后续研究中将使用更真实表现土体非线性行为的本构模型及真实工程场地参数。算例中的大气压参数取100kPa，内摩擦角增量取0°。入射地震动分别选取狄拉克脉冲和实测地震动（Gilroy Array #3，Coyote Lake, 1979）。入射狄拉克脉冲见图 3，观测点结果见图 4，实测地震动见图 5，观测点结果见图 6。图 4、图 6中给出采用中心差分法的计算结果作为参考解，由图 4、图 6可知，本文算法与中心差分法计算结果吻合较好，说明本文算法的有效性。
图 2 大开车站沿线土层纵断面构造Figure 2. Site condition of the Daikai subway station in vertical direction表 1 土层参数Table 1. Parameters of soils土质 深度/
m$\rho $/
（g/cm3）cs /
（m/s）v
-EN
-Rf
-c/
（MPa）θ/（°） D
-F
-人工填土 0—1.0 1.9 140 0.33 0.33 0.758 0.084 26.9 1.06 0.021 全新世砂土 1.0—5.1 1.9 140 0.32 0.33 0.758 0.084 26.9 1.06 0.021 全新世砂土 5.1—8.3 1.9 170 0.32 0.36 0.768 0.120 31.0 1.11 0.015 更新世粘土 8.3—11.4 1.9 190 0.40 0.44 0.822 0.188 28.4 1.01 0.012 更新世粘土 11.4—17.2 1.9 240 0.30 0.44 0.822 0.188 28.4 1.01 0.012 更新世砂土 17.2—22.2 2.0 330 0.26 0.51 0.840 0.300 30.0 1.02 0.011 基岩 ＞22.2 2.0 330 0.26 - - - - - - 
图 3 狄拉克脉冲速度和加速度时程图Figure 3. Velocity and acceleration time history of the Dirac pulse
图 4 狄拉克脉冲入射时场地反应分析结果Figure 4. Results of site analysis under the incident of Dirac pulse
图 5 实测地震动速度和加速度时程图Figure 5. Velocity and acceleration time history of the seismic motion
图 6 实测地震动入射时场地反应分析结果Figure 6. Results of site reaction analysis under the incident of the seismic motion表 1中ρ、cs、v、EN、Rf、c、θ为模型参数，分别表示密度、剪切波速、泊松比、无量纲幂次、破坏比、土的内聚力、土的摩擦角。D、F为试验常数。
3. 结论
本文发展一种求解材料非线性结构动力学方程的显式时间积分算法，并应用于地震波竖直入射时非线性地震反应分析中，通过算例验证了该方法的有效性。该显式算法具有无需对角阻尼矩阵、单步、稳定性良好等优点。本文考虑了邓肯-张非线性弹性本构模型，下步研究可考虑将该显式算法扩展到弹塑性本构模型及更能反映土层真实变形的本构模型中。
-
图 1 青岛地区地质构造图
F1：沧口断裂；F2：青岛山断裂；F3：劈石口断裂；F4：王哥庄断裂；F5：马山-王哥庄断裂
Figure 1. Simplified geological map of the Qingdao area
图 2 不同道间距的超浅层地震共炮点记录
Figure 2. The common-shot gather of ultra-shallow seismic records in different trace intervals
图 3 原始数据及不同信噪比下的f-k滤波对比及其频谱分析图（一）
Figure 3. Analysis between f-k filtering under different signal-to-noise ratio data and corresponding spectrum
图 4 TEST-a地震反射时间及地质解释剖面
Figure 4. Stack time section of seismic reflection and the interpretation in TEST-a
图 5 TEST-b地震反射时间及地质解释剖面
Figure 5. Stack time section of seismic reflection and the interpretation in TEST-b
图 6 TEST-a和TEST-b测线王哥庄断裂钻孔联合地质剖面
Figure 6. The drilling geological section of WGZ fracture combined with the TEST-a and TEST-b survey lines
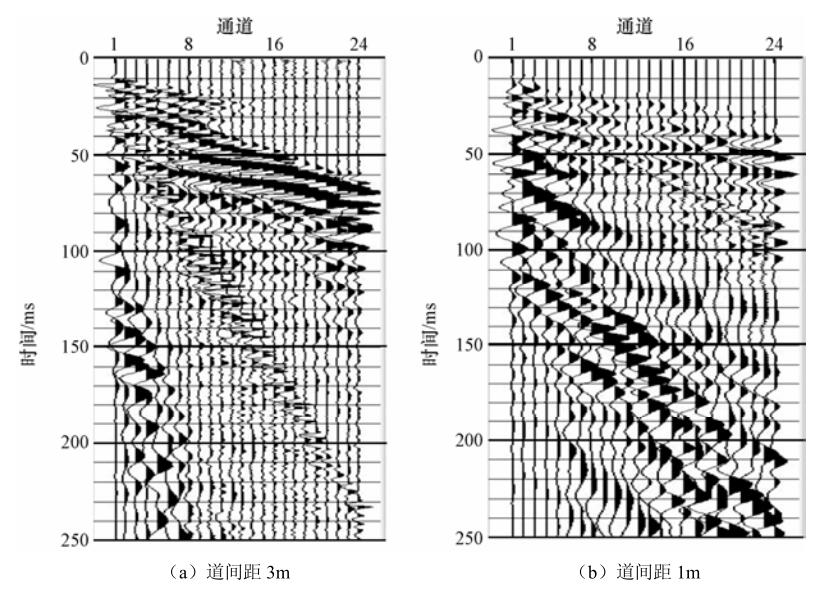
表 1 观测系统参数和地震采集参数表
Table 1. Survey parameters and seismic data acquisition details
剖面编号 道间距/m 偏移距/m 接收道数 覆盖次数 激发震源 检波器固有频率/Hz 采样间隔/ms 记录长度/ms TEST-a 3 6 24 6 人工夯击 60 0.25 256 TEST-b 1 7 24 12 人工锤击 100 0.25 256 
下载: 导出CSV
-
陈颙, 陈龙生, 于晟, 2003.城市地球物理学发展展望.大地测量与地球动力学, 23(4):1-4. https://www.wenkuxiazai.com/doc/f997f82a915f804d2b16c15d.html 邓起东, 2002.城市活动断裂探测和地震危险性评价问题.地震地质, 24(4):601-605. http://mall.cnki.net/magazine/Article/DZDZ200204015.htm 邓起东, 徐锡伟, 张先康等, 2003.城市活动断裂探测的方法和技术.地学前缘, 10(1):93-104. http://www.cnki.com.cn/Article/CJFDTOTAL-DXQY200301019.htm 段生全, 贺振华, 黄德济, 2005.HHT方法及其在地震信号处理中的应用.成都理工大学学报(自然科学版), 32(4):396-400. http://www.cnki.com.cn/Article/CJFDTOTAL-CDLG200504013.htm 方盛明, 张先康, 刘保金等, 2002.探测大城市活断层的地球物理方法.地震地质, 24(4):606-613. http://www.cnki.com.cn/Article/CJFDTOTAL-DZDZ200204016.htm 何正勤, 陈宇坤, 叶太兰等, 2007.浅层地震勘探在沿海地区隐伏断层探测中的应用.地震地质, 29(2):363-372. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dzdz200702014 何正勤, 潘华, 胡刚等, 2010.核电厂址隐伏断裂探测中的地震勘探方法研究.地球物理学报, 53(2):326-334. http://manu39.magtech.com.cn/Geophy/CN/abstract/abstract1271.shtml 李大虎, 何强, 邵昌盛等, 2010.综合地球物理勘探在青川县城区活动断层探测中的应用.成都理工大学学报(自然科学版), 37(6):666-672. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cdlgxyxb201006012 李万伦, 刘素芳, 田黔宁等, 2018. 城市地球物理学综述. 地球物理学进展. (2018-01-25)http://kns.cnki.net/kcms/detail/11.2982.P.20180125.1015.018.html 刘保金, 张先康, 方盛明等, 2002.城市活断层探测的高分辨率浅层地震数据采集技术.地震地质, 24(4):524-532. http://www.cnki.com.cn/Article/CJFDTOTAL-DZDZ200204006.htm 潘纪顺, 刘保金, 朱金芳等, 2002.城市活断层高分辨率地震勘探震源对比试验研究.地震地质, 24(4):533-541. http://www.cqvip.com/QK/95728X/200204/7297242.html 许汉刚, 范小平, 冉勇康等, 2016.郯庐断裂带宿迁段F5断裂浅层地震勘探新证据.地震地质, 38(1):31-43. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dzdz201601003 徐明才, 高景华, 刘建勋等, 2005.应用于城市活断层调查的地震方法技术.中国地震, 21(1):17-23. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgdz200501002 杨歧焱, 彭远黔, 尼玛等, 2015.日喀则城市活断层地球物理勘探方法和成果.地球物理学报, 58(6):2137-2147. doi: 10.6038/cjg20150627 杨歧焱, 彭远黔, 周月玲等, 2016.综合地质-地球物理方法在山间盆地断裂探测中的应用——以张家口断裂为例.地球物理学进展, 31(6):2451-2457. doi: 10.6038/pg20160613 杨晓平, 郑荣章, 张兰凤等, 2007.浅层地震勘探资料地质解释过程中值得重视的问题.地震地质, 29(2):282-293. https://www.wenkuxiazai.com/doc/fad75423192e45361066f5f7-2.html 朱金芳, 徐锡伟, 张先康等, 2005.福州盆地及邻区地壳精细结构的深地震反射与高分辨率折射及宽角反射/折射联合探测研究.中国科学D辑地球科学, 35(8):738-749. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_zgkx-cd200508006 Williams R. A., Odum J. K., Pratt T. L., et al., 1995. Seismic surveys assess earthquake Hazard in the New Madrid area. The Leading Edge, 14(1):30-34. doi: 10.1190/1.1437060 -
下载:
点击查看大图
计量
- 文章访问数: 122
- HTML全文浏览量: 13
- PDF下载量: 14
- 被引次数: 0
