地震作用下场地有限元建模时底部边界条件的影响

白建方; 董士欣

doi:10.11899/zzfy20180104

地震作用下场地有限元建模时底部边界条件的影响

doi: 10.11899/zzfy20180104

石家庄铁道大学土木工程学院, 石家庄 050043

基金项目: 河北省大型基础设施防灾减灾协同创新中心项目和河北省重点学科建设项目(桥梁与隧道工程)

详细信息

作者简介:
白建方, 男, 生于1976年。博士, 讲师。主要从事工程系统抗震方面的研究。E-mail:bjf2004@126.com

计量
- 文章访问数: 59
- HTML全文浏览量: 39
- PDF下载量: 5
- 被引次数: 0
出版历程
- 收稿日期: 2017-03-20
- 刊出日期: 2018-03-01

The Effect of the Bottom Boundary Condition on Site Finite Element Modeling under Earthquake Load

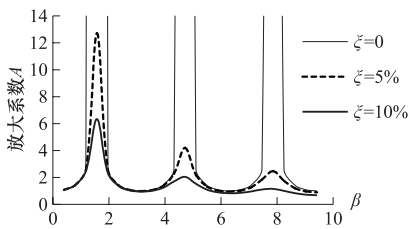
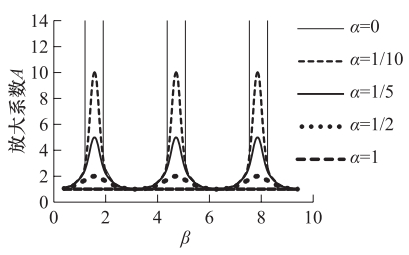
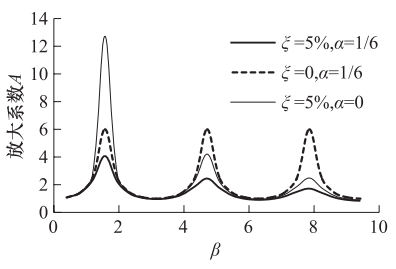
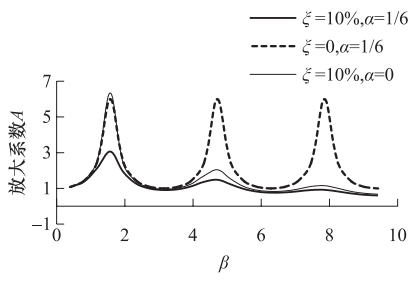
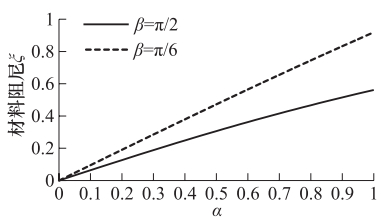
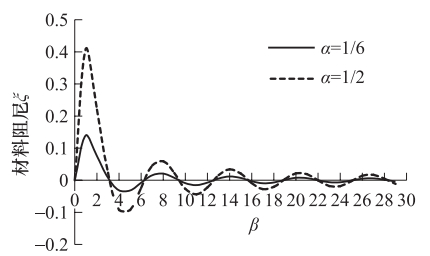
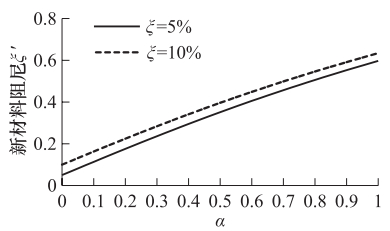
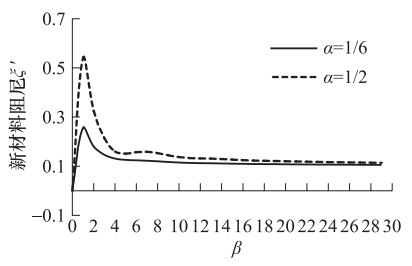
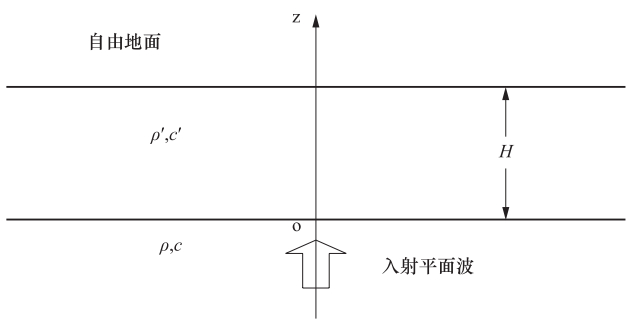
Shijiazhuang Tiedao University, Shijiazhuang 050043, China

摘要

摘要: 用有限元方法对场地进行地震反应分析时需将半无限域的场地有限化。本文针对底部人工边界的设置，采用滞回阻尼假设，推导了同时包含辐射阻尼和材料阻尼的均质场地地表位移放大系数解析式，进而研究了材料阻尼和辐射阻尼的变化对放大系数的影响。有限元建模时相当于忽略了辐射阻尼，计算误差会随着所分析场地阻抗的增加而逐渐增大，在共振区附近，忽略任一种阻尼的影响，都将显著地高估地表动力反应；远离共振区，阻尼的影响会迅速衰退。本文提出了通过增加场地材料阻尼来弥补所忽略的辐射阻尼的思路，并给出了有限元建模时考虑辐射阻尼后新的材料阻尼的确定方法。
- 底部人工边界条件 /
- 场地地震反应分析 /
- 有限元方法 /
- 辐射阻尼 /
- 材料阻尼
Abstract: The actual site is a semi-infinite space and not only on the horizontal direction, but also on the downward are infinitely.In order to build the numerical model for site through direct finite element method, we have to account the artificial boundary conditions first because it is the foundation of how to consider the scope of soil site.In common used method the interface between overlaying bedrock and soil is assumed to be the fixed bottom boundary.In order to find the effect created from this bottom boundary condition, in this paper we performed the theoretical analysis and numerical tests.On this base, we studied the effect of the radiation damping and material damping on the site dynamic response under earthquake load, and it would be possible to decrease the influence of the bottom boundary condition by increases the material damping.
- The bottom boundary condition /
- Site earthquake response analysis /
- Finite element method /
- Radiation damping /
- Material damping

HTML全文

图 1 理论模型

Figure 1. Theoretical model

下载: 全尺寸图片幻灯片

图 2 材料阻尼的影响

Figure 2. The effect of the material damping

下载: 全尺寸图片幻灯片

图 3 辐射阻尼的影响

Figure 3. The effect of the radiation damping

下载: 全尺寸图片幻灯片

图 4 共振时放大系数随α的变化规律

Figure 4. The change of the amplification with α under β=π/2

下载: 全尺寸图片幻灯片

图 5 ξ＝5%的结果

Figure 5. The result for ξ＝5%

下载: 全尺寸图片幻灯片

图 6 ξ＝10%的结果

Figure 6. The result for ξ＝10%

下载: 全尺寸图片幻灯片

图 7 材料阻尼随α的变化

Figure 7. The change of the material damping with α

下载: 全尺寸图片幻灯片

图 8 材料阻尼随β的变化

Figure 8. The change of the material damping with β

下载: 全尺寸图片幻灯片

图 9 新的材料阻尼比随α的变化

Figure 9. The change of the new material damping with α

下载: 全尺寸图片幻灯片

图 10 新材料阻尼随β的变化

Figure 10. The change of the new material damping with β

下载: 全尺寸图片幻灯片

图 11 场地有限元模型

Figure 11. The finite element model of site

下载: 全尺寸图片幻灯片

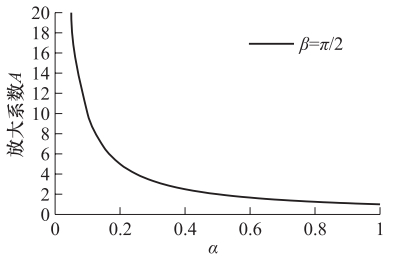
表 1 共振时的地表动力放大系数

Table 1. The amplification under β=π/2

参数	ξ＝0	ξ＝5%	ξ＝10%	ξ＝15%
α＝0	+∞	12.72	6.34	4.21
α＝1/10	10	5.59	3.86	2.94
α＝1/5	5	3.58	2.78	2.56
α＝1/2	2	1.72	1.51	1.33
α＝1	1	0.92	0.86	0.79

下载: 导出CSV

参考文献(11)

陈昌斌, 楼梦麟, 陶寿福, 2006.二维场地地震反应有限元分析的问题探讨.震灾防御技术, 1(4):292-301. doi: 10.11899/zzfy20060402

戴国莹, 王亚勇, 2005.房屋建筑抗震设计.北京:中国建筑工业出版社.

李建亮, 李福海, 彭晋川等, 2015.不同的地震动输入面对地震反应分析结果的影响.震灾防御技术, 10(3):522-530. doi: 10.11899/zzfy20150305

廖振鹏, 2002.工程波动理论导论.北京:科学出版社.

刘志祥, 张海清, 2015.PLAXIS高级应用教程.北京:机械工业出版社.

楼梦麟, 潘旦光, 范立础, 2003.土层地震反应分析中侧向人工边界的影响.同济大学学报, 31(7):757-761. https://www.wenkuxiazai.com/doc/bbcdd18002d276a200292efa.html

潘旦光, 楼梦麟, 2004.基岩弹性刚度对土层地震反应的影响.地震工程与工程振动, 24(4):158-163. http://cqvip.com/QK/95324X/200602/21209772.html

萨瓦林斯基, 1981. 地震波. 段星北, 译. 北京: 科学出版社.

沈建文, 2004.上海市地震动参数区划.北京:地震出版社.

Bielak, J.and P.Christiano, 1984.On the effective seismic input for non-linear soil-structure interaction system.Earthquake Eng.Struct.Dyn., 12, 107-119. doi: 10.1002/(ISSN)1096-9845

Wolf J.P., 1985.Dynamic soil-structure interaction.New Jersey:Prentice-Hall.

施引文献

资源附件(0)

访问统计