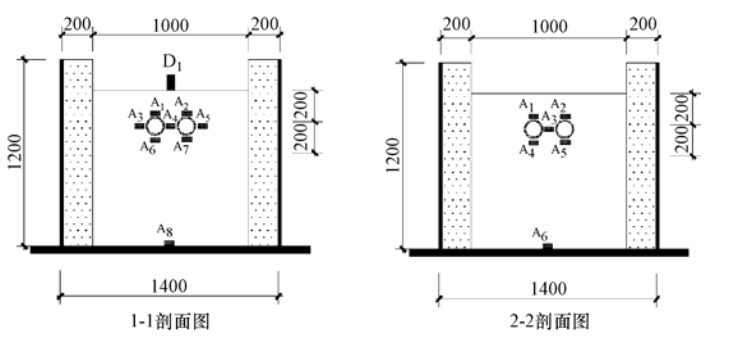
Study on the Scheme of Sensor Position in Shaking Table Test for Long Distance Buried Pipeline
-
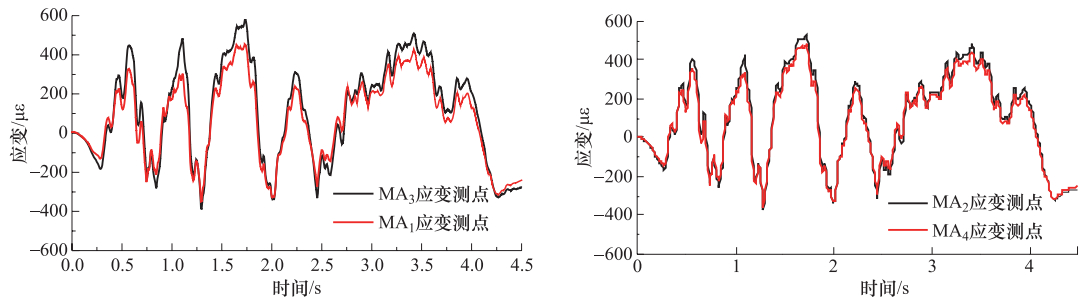
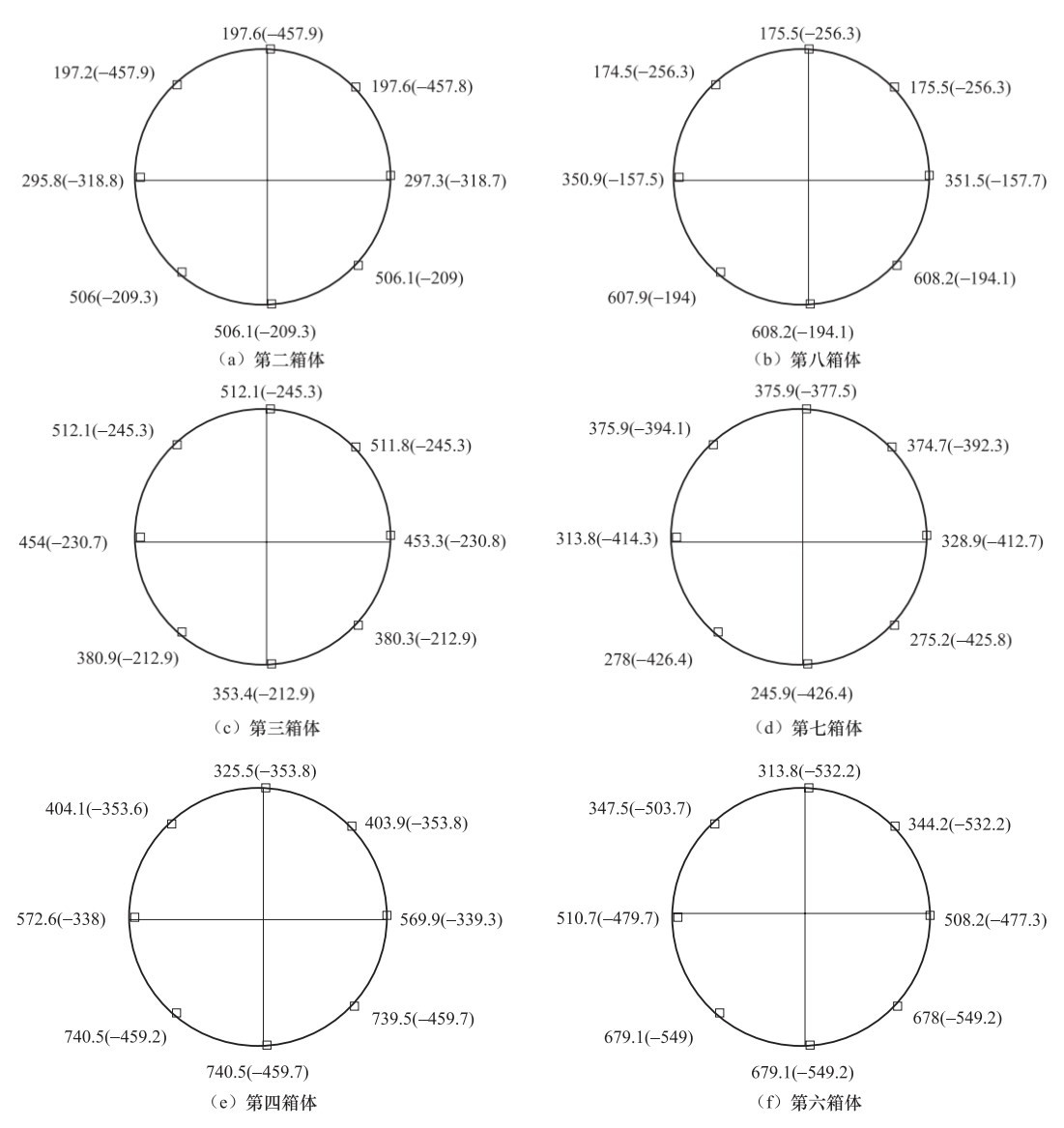
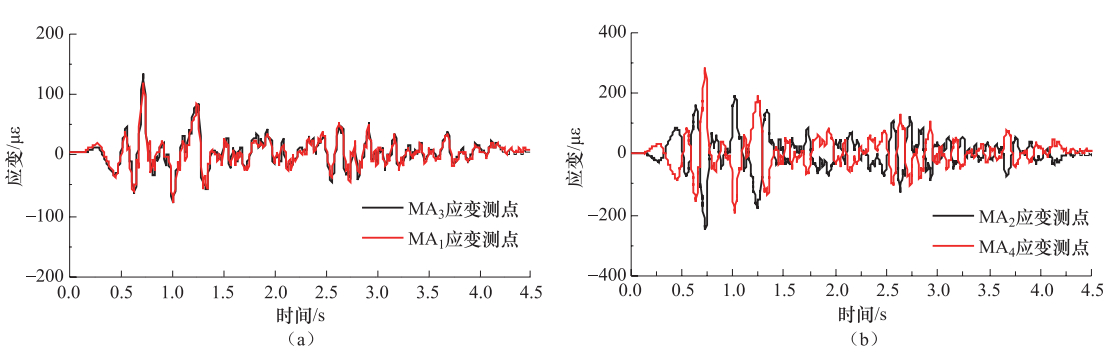
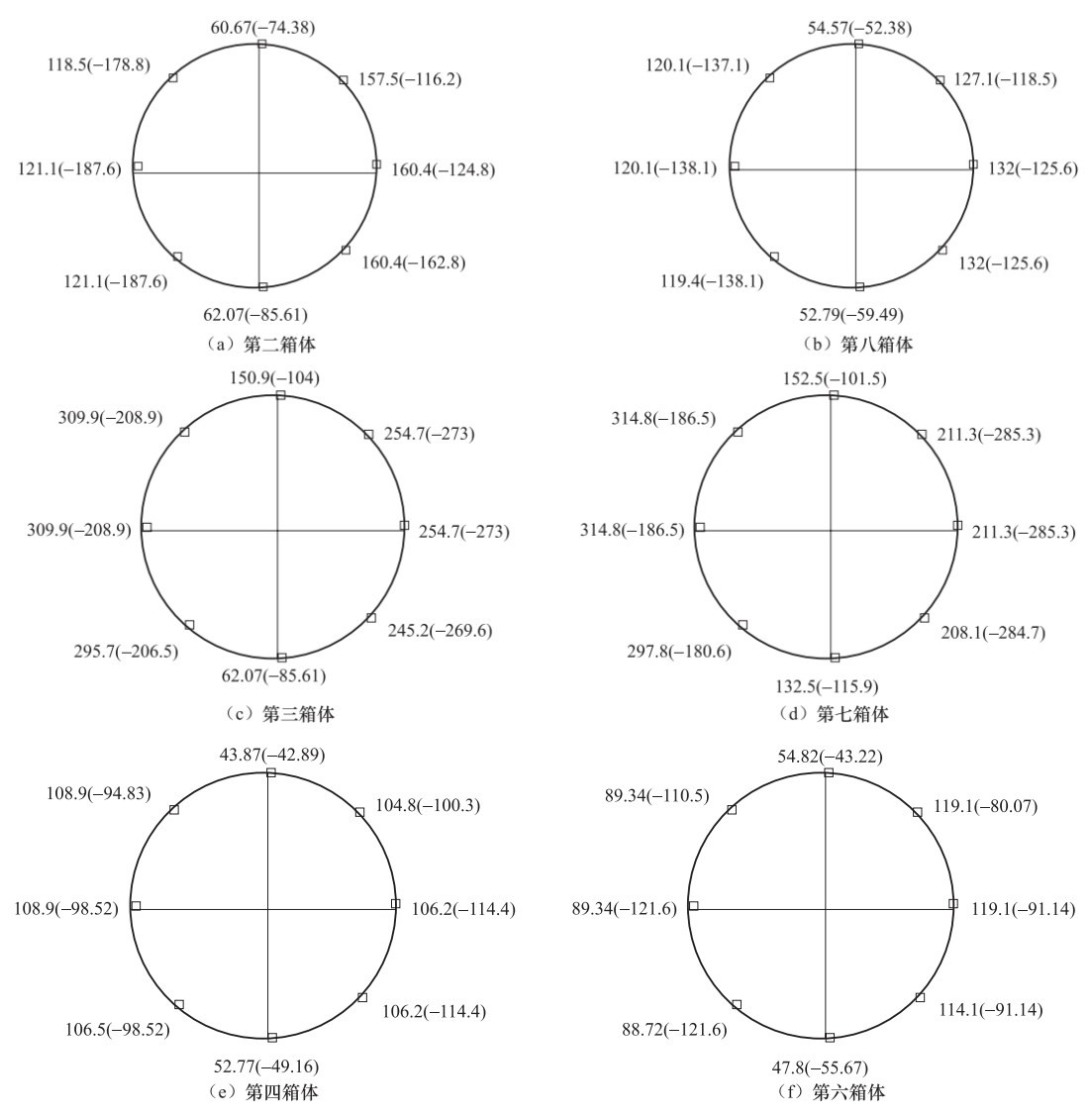
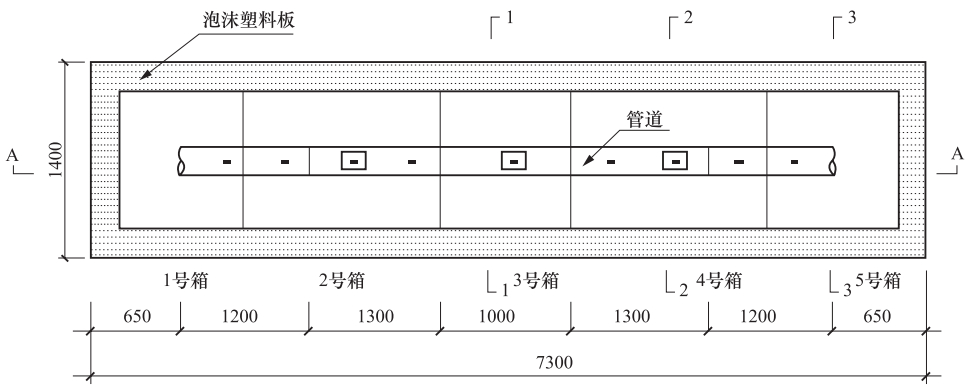
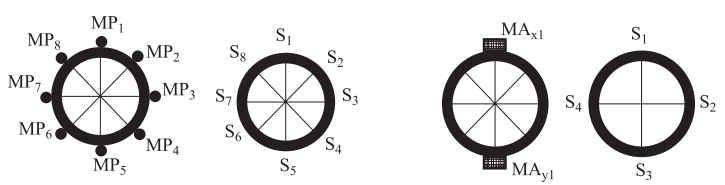
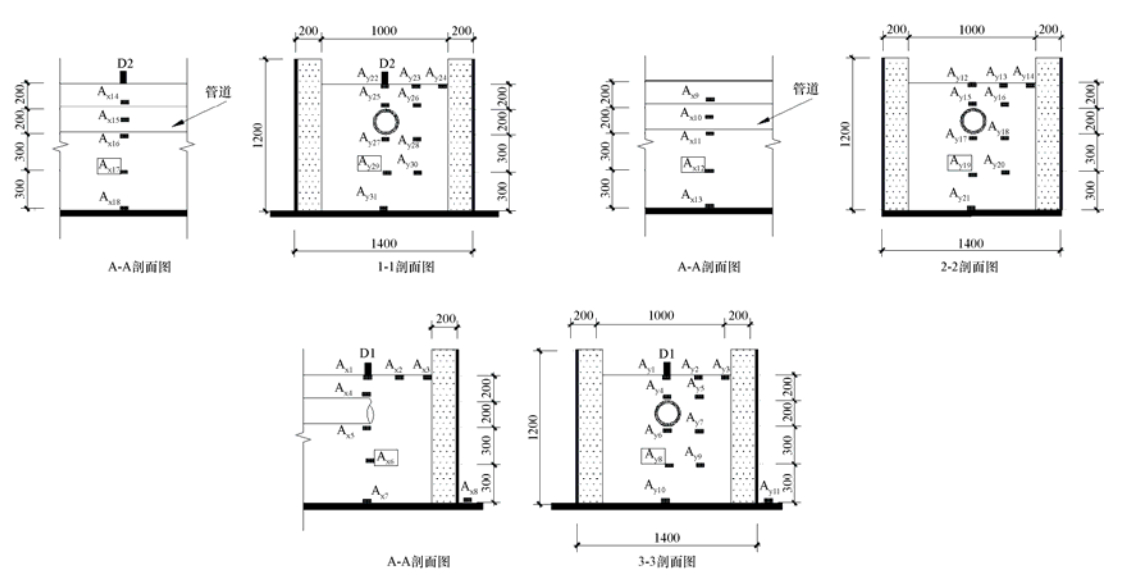
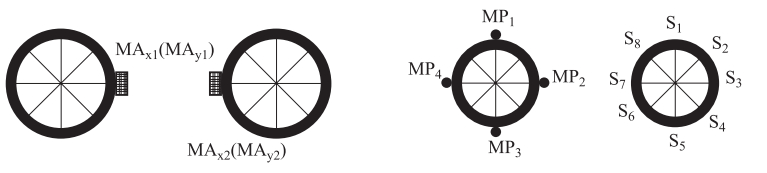
摘要: 在进行长输埋地管道振动台试验的过程中，针对数据信息的采集量测以及传感器的布置位置进行了研究。采用三维数值模拟的方法对管-土相互作用体系进行了地震反应分析，内容包括埋地管道结构纵、横向在非一致地震动作用下的地震响应及受力变形特征。根据计算结果确定了主观测断面及辅助观测断面的位置及观测断面上传感器布置的位置，在满足基本信息采集要求的前提下，对可供采用的信息采集通道进行了优化分配，由此确定本次试验的观测断面以及传感器的具体测量部位与数目。成果对试验获得成功起到了保障作用，可为同类试验提供参考。Abstract: The location scheme of the sensors in a shaking table test for a long distance buried pipeline was studied in this paper.The seismic response analyses of pipe-soil interaction were performed in this study by using a 3-D finite element model of the buried pipeline.The seismic response and dynamic characteristics of the buried pipeline under longitudinal and lateral ground motions were carefully investigated and subsequently used to determine the locations of the critical sections and auxiliary sections for deploying sensors.The location schemes of the sensors on those sections were selected according to the numerical results.The data acquisition channels were also optimized in order to effectively record necessary data during the tests.The monitoring sections as well as the number and location of the sensor were finally determined.The scheme of sensor locations played an important role in guaranteeing the success of the experiment, and also has some reference values for similar experiments in the future.
-
Key words:
- Buried pipeline /
- Shaking table test /
- Sensor location
-
图 1 模型箱土仿真模型及管道数据测点
Figure 1. The simulation model of the model box and soil, and data points of the buried pipeline
图 2 纵向El Centro地震动应变时程
Figure 2. Strain time histories of longitudinal El Centro earthquake
图 3 纵向非一致激励下管周应变(单位：με)
Figure 3. Circumference strain under longitudinal non-uniform seismic excitations (unit: με)
图 4 横向El Centro地震动应变时程
Figure 4. Strain time histories of transverse El Centro ground motion
图 5 横向非一致激励下管周应变(单位：με)
Figure 5. Circumference strain under transverse non-uniform seismic excitations (unit: με)
图 6 非自由场试验各观测面位置
Figure 6. The observation surface position of the non-free field test
图 8 非自由场试验各观测面传感器布置
Figure 8. Sensor arrangement on the observation surface in the non-free field test
图 9 非自由场振动台试验各观测面位置
Figure 9. The observation surface position in the non-free field test
表 1 管-土结构模型相似关系
Table 1. Similitude relation of pipeline structure models
类型 Sl SE Sρ Sσ Sε ST Sf Sν Sa 管 1/10 1/65 1/6.5 1/65 1 0.316 3.16 0.316 1 土 1/10 1/4 1/1 1/4 1 1/5 5 1/2 2.5 
下载: 导出CSV
-
杜修力, 韩俊艳, 李立云, 2013.长输埋地管道振动台试验设计中相似关系的选取.防灾减灾工程学报, 33(3):246-252. http://xueshu.baidu.com/s?wd=paperuri%3A%28382f33343c3946a906a8d5ab19ce2a10%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fkns.cnki.net%2FKCMS%2Fdetail%2Fdetail.aspx%3Ffilename%3Ddzxk201303003%26dbname%3DCJFD%26dbcode%3DCJFQ&ie=utf-8&sc_us=306167632782111102 韩俊艳, 杜修力, 李立云, 2013.土工振动台试验连续体模型箱的适用性研究.地震工程与工程振动, 33(2):200-208. http://tjz.docin.com/p-1087479617.html 李德寅, 王邦楣, 林亚超, 1996.结构模型实验.北京:科学出版社. 李杰, 2005.生命线工程抗震-基础理论与应用.北京:科学出版社. 刘祥庆, 刘晶波, 王宗纲, 2008.土-结构动力离心模型试验传感器位置的优选.清华大学学报(自然科学版), 48(6):931-935. http://www.cqvip.com/QK/93884X/200806/27618655.html 权登州, 王毅红, 井彦林等, 2015.黄土地区地铁车站数值模型及测试位置研究.震灾防御技术, 10(1):108-115. doi: 10.11899/zzfy20150111 杨林德, 季倩倩, 杨超等, 2004.地铁车站结构振动台试验中传感器位置的优选.岩土力学, 25(4):619-623. https://www.wenkuxiazai.com/doc/d125accd9ec3d5bbfd0a742e.html 杨旭东, 2005.振动台模型试验若干问题的研究.北京:中国建筑科学研究院. 庄海洋, 陈国兴, 杜修力等, 2007.液化大变形条件下地铁车站结构动力反应大型振动台试验研究.地震工程与工程振动, 27(4):94-97. https://www.wenkuxiazai.com/doc/3f27ec4577232f60ddcca167.html -
点击查看大图
计量
- 文章访问数: 81
- HTML全文浏览量: 37
- PDF下载量: 5
- 被引次数: 0
