Experimental Research on Dynamic Shear Modular Ratio and Damping Ratio of Sandy Gravel Soil
-
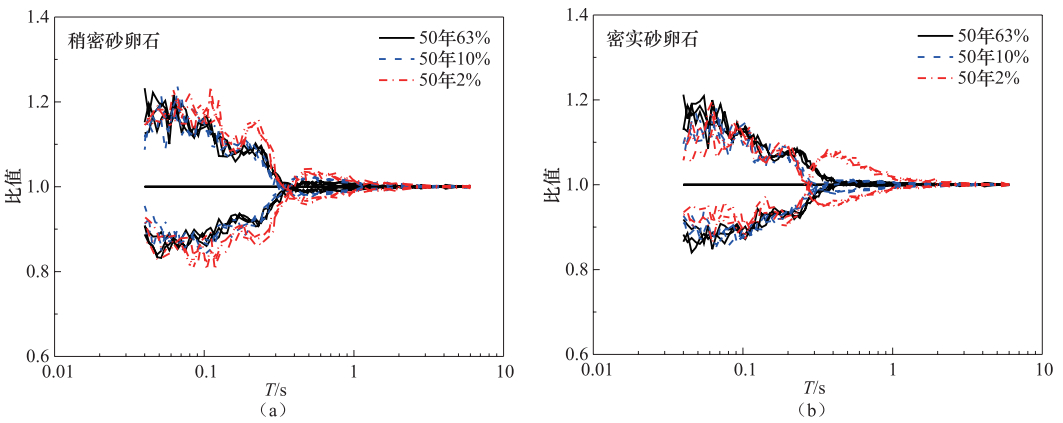
摘要: 砂卵(砾)石的动剪切模量比和阻尼比是河谷地貌场地地震反应分析的重要参数，对设计地震动参数的确定有重要影响。本文利用商洛市地震小区划项目砂卵石的动三轴试验结果，结合其他砂卵(砾)石动三轴试验结果，分组统计得到了稍密、中密、密实砂卵(砾)动三轴试验的推荐结果。建立了典型场地模型，研究了其动剪切模量比和阻尼比的不确定性对场地地震反应的影响。研究表明：动剪切模量比、阻尼比平均值±1倍标准差的不确定性对砂卵石场地峰值加速度的影响较小，说明了分组及统计结果的合理性；不同概率水平下，动剪模量比、阻尼比的变化导致高频部分反应谱有明显差异，0.04-0.1s的反应谱变化范围在20%左右，但对大于1.0s的长周期反应谱影响很小。针对砂卵(砾)石动剪切模量比和阻尼比的研究对提高工程场地设计地震动参数的可靠性具有重要意义。Abstract: The dynamic shear modulus ratio and damping ratio of sand gravel are important parameters for seismic response analysis of valley geomorphic sites, which have an important impact on the determination of design ground motion parameters.In this paper, based on the project of Shangluo Seismic Microzonation, the dynamic triaxial test of sandy pebbles has been performed.Combined with the other results of sandy gravel, the recommended results of slightly dense, medium dense and dense sandy gravel were obtained.By building the typical site model, the influence of the dynamic shear modulus ratio and the damping ratio uncertainty on the seismic response of the site is studied.The results show that the uncertainty of the average of the dynamic shear modulus ratio and the damping ratio ±1 times the standard deviation has little effect on the peak acceleration of the sandy pebble site, and the rationality of the grouping and statistical results is explained.Under different probability levels, the change of shear modulus ratio and damping ratio leads to a significant difference in the response spectrum of high frequency.The response spectrum of 0.04-0.1s range from about 20%, but it has little effect on the long period spectrum of more than 1.0s.The study of dynamic shear modulus ratio and damping ratio of sandy gravel has great significance to improve the reliability of the designing ground motion parameters.
-
引言
地震前兆观测主要关注观测数据随时间的相对变化，装置系数误差不影响观测数据的相对变化，但不正确的装置系数可能导致地电阻率观测结果出现系统误差（王兰炜等，2014），因此，正确的装置系数有利于不同区域观测数据的对比和地震前兆数据的研究。自2009年起，河北大柏舍台，甘肃天水台、武都台、平凉台，陕西合阳台实施了井下地电阻率垂直观测试验，井孔深100—225m，供电极距60—120m，测量极距20—60m（刘君等，2015；王兰炜等，2015）。上述台站地电阻率垂向观测通常为1个钻孔，供电电极和测量电极均布设于1个钻孔中，部分垂向观测的供电电极A接近地表，如天水台、武都台、合阳台的供电电极A埋深仅4—5m；部分垂向观测的供电电极A埋深为40m左右，如大柏舍台。垂向地电阻率观测中的装置系数与电流的空间分布及电极位置有关，现有垂向观测装置系数计算方法依据地下点、地表点电流源产生的电场计算得出，忽略了供电电极A的埋深。江宁台深井垂向地电阻率观测装置为在2口深井进行垂向观测的试验装置，与传统垂向地电阻率观测装置不同。本文根据地下点电流源产生的电场讨论装置系数计算方法，并比较计算方法对江宁台垂向地电阻率观测的影响。
1. 台址概况
江宁台地处南京市江宁区禄口街道水荆墅村，地形开阔平坦，周围无大中型工矿企业，测区位于南京-湖熟断裂南西盘和方山-小丹阳断裂西盘的楔形地块上，东距茅山断裂带30km，西北距长江36km。测区内现有垂向地电阻率观测装置为在2口深井进行垂向观测的试验装置，井距5.17m，供电电极A、测量电极M分别布设在深275m的2号井内200m和275m处，供电电极B、测量电极N分别布设在深400m的1号井内400m和325m处（图 1）。该垂向观测系统采用ZD8BI型地电仪，根据《地震台站建设规范（地电台站第1部分）》（DB/T.18.1—2006）中关于地电阻率台站的技术要求，对新建垂向观测装置的场地进行高密度电法、电测深等测试。高密度电法探测和电测深报告中NW—SE和NS测线结果表明，观测区域电测深曲线具有K形特征，电性结构等效为3层（樊晓春等，2018），场地电性层参数见表 1。
表 1 江宁台场地电性层参数Table 1. The underground electrical structure of Jiangning geoelectric stationNW—SE测线 NS测线 层厚/m 电阻率/Ω·m 层厚/m 电阻率/Ω·m 29.40 39.29 24.56 18.71 220.94 143.06 203.42 274.52 ∞ 60.39 ∞ 54.79 2. 点电流源在非全空间产生的电场
点电流处于不完全全空间时，对点电流源位于地下和地表 2种情况进行讨论。地下点电流源产生的电场指点电流源的电流I在地下一定深度时流入地下介质中产生的电场，为不完全全空间。假设地下介质电性均匀，介质电阻率为ρ，电流I从地下A点流入（图 2），采用镜像法计算（刘昌谋等，1994；刘国兴，2005），见式（1）。地表点电流源产生的电场指地表点电流源电流I流入地下介质，从无限远处流出时在介质中产生的电场，为半无限空间。假设地下介质电性均匀，介质电阻率为ρ，电流I从地表A点流入地下，电流线的分布以A为中心向周围呈辐射状，该情况为图 2的特例（王兰炜等，2014），见式（2）。
图 2 地下点电源产生的电场示意图Figure 2. The schematic diagram of the electric field generated by underground point power supply（1）地下点电流源产生的电场（不完全全空间）
$$ {V_{{\rm{MN}}}} = \frac{{\rho I}}{{4{\rm{ \mathsf{ π} }}}}\left({\frac{1}{{\overline {AM} }} + \frac{1}{{\overline {{A_1}M} }} - \frac{1}{{\overline {{A_1}N} }} - \frac{1}{{\overline {AN} }}} \right) $$ (1) （2）地表点电流源产生的电场（半无限空间）
$$ {V_{{\rm{MN}}}} = \frac{{\rho I}}{{2{\rm{ \mathsf{ π} }}}}\left({\frac{1}{{\overline {AM} }} - \frac{1}{{\overline {AN} }}} \right) $$ (2) 3. 装置系数计算方法
装置系数是地电阻率观测中特有的参数，通常用K表示，与观测装置中电极分布情况有关，表征地电阻率是视电阻率（王兰炜等，2014）。当测区区域介质电阻率均匀分布时，地电阻率ρs与介质真实的电阻率ρ数值相同。
根据奥斯定理和镜像原理（钱家栋等，1985），假设测区为均匀介质，垂向观测中的装置系数计算方法如下：
（1）方法Ⅰ：传统垂向观测装置系数计算方法（王兰炜等，2014）
传统方法井下垂向观测装置忽略电极A的埋深，在点电源B与地面对称的位置设镜像点B1，见图 3（a）。根据式（1）和式（2），则K为：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\left({\frac{2}{{\overline {AM} }} - \frac{2}{{\overline {AN} }}} \right) - \left({\frac{1}{{\overline {BM} }} + \frac{1}{{\overline {{B_1}M} }} - \frac{1}{{\overline {{B_1}N} }} - \frac{1}{{\overline {BN} }}} \right)}} $$ (3) 不考虑江宁台垂向观测电极A埋深时，因江宁台垂向观测AM=BN，AN=BM，则：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\frac{3}{{\overline {AM} }} - \frac{3}{{\overline {AN} }} - \frac{1}{{\overline {{B_1}M} }} + \frac{1}{{\overline {{B_1}N} }}}} $$ (4) （2）方法Ⅱ：采用全空间方式的装置系数计算方法（钱家栋等，1985；王兰炜等，2014）
当电极埋深h远大于供电极长度AB时，为全空间，则K为地表观测装置系数的2倍，即：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\frac{1}{{\overline {AM} }} - \frac{1}{{\overline {AN} }} - \frac{1}{{\overline {BM} }} + \frac{1}{{\overline {BN} }}}} $$ (5) （3）方法Ⅲ：采用不完全全空间方式的装置系数计算方法
江宁台垂向观测的电极A、M、N、B分别位于埋深200m、275m、325m、400m处，应按地下点电源产生的电场模型计算（不完全全空间），如图 3（b）所示。在点电源A、B与地面对称的位置设镜像点A1、B1，忽略1号井和2号井的水平距离l，根据式（1），则供电电流I（+I和-I）在M、N间产生的电位差为：
$$ {V_{MN}} = \frac{{\rho I}}{{4{\rm{ \mathsf{ π} }}}}\left[ {\left({\frac{1}{{\overline {AM} }} + \frac{1}{{\overline {{A_1}M} }} - \frac{1}{{\overline {{A_1}N} }} - \frac{1}{{\overline {AN} }}} \right) - \left({\frac{1}{{\overline {BM} }} + \frac{1}{{\overline {{B_1}M} }} - \frac{1}{{\overline {{B_1}N} }} - \frac{1}{{\overline {BN} }}} \right)} \right] $$ (6) 则K为：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\left({\frac{1}{{\overline {AM} }} + \frac{1}{{\overline {{A_1}M} }} - \frac{1}{{\overline {AN} }} - \frac{1}{{\overline {{A_1}N} }}} \right) - \left({\frac{1}{{\overline {BM} }} + \frac{1}{{\overline {{B_1}M} }} - \frac{1}{{\overline {BN} }} - \frac{1}{{\overline {{B_1}N} }}} \right)}} $$ (7) 因江宁台垂向观测AM=BN，AN=BM，则：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\frac{2}{{\overline {AM} }} - \frac{2}{{\overline {AN} }} + \frac{1}{{\overline {{A_1}M} }} - \frac{1}{{\overline {{A_1}N} }} - \frac{1}{{\overline {{B_1}M} }} + \frac{1}{{\overline {{B_1}N} }}}} $$ (8) （4）方法Ⅳ：采用不完全全空间方式（考虑井距l）的装置系数计算方法
按照地下点电源产生电场的模型计算（不完全全空间），在点电源A、B与地面对称的位置设镜像点A1、B1，h1、h2、h3表示供电电极A、B、M的电极埋深，井距l表示2口井孔水平距离（图 3（c）），则：
$$ \overline {AM} = {h_3} - {h_1} $$ (9) $$ \overline {AN} = \sqrt {{l^2} + {{({h_2} - {h_3})}^2}} $$ (10) $$ \overline {{A_1}M} = {h_1} + {h_3} $$ (11) $$ \overline {{A_1}N} = \sqrt {{l^2} + {{({h_2} + 2{h_1} - {h_3})}^2}} $$ (12) $$ \overline {{B_1}M} = \sqrt {{l^2} + {{({h_2} + {h_3})}^2}} $$ (13) $$ \overline {{B_1}N} = 2{h_2} - {h_3} + {h_1} $$ (14) 将式（9）至式（14）代入式（8），则K变为：
$$ K = \frac{{4\pi }}{{\frac{2}{{{h_3} - {h_1}}} - \frac{2}{{\sqrt {{l^2} + {{({h_2} - {h_3})}^2}} }} + \frac{1}{{{h_1} + {h_3}}} - \frac{1}{{\sqrt {{l^2} + {{({h_2} + 2{h_1} - {h_3})}^2}} }} - \frac{1}{{\sqrt {{l^2} + {{({h_2} + {h_3})}^2}} }} + \frac{1}{{2{h_2} - {h_3} + {h_1}}}}} $$ (15) 4. 江宁台垂向地电阻率观测装置系数计算
采用方法Ⅰ—Ⅳ分别计算江宁台垂向地电阻率观测的装置系数K，结果见表 2。考虑江宁台垂向地电阻率观测的电极布设不同于传统垂向观测装置，所有电极埋深均在200m以上，本文认为应以方法Ⅳ为参考值，采用式（16）计算不同装置系数计算方法的相对误差。方法Ⅰ、Ⅱ、Ⅲ相对误差分别为-32.01%、1.37%、0.43%，可知方法Ⅰ不适用于江宁台垂向地电阻率观测，该计算方法通常仅适用于供电电极A埋深小于5m的垂向观测，如天水台、合阳台。方法Ⅱ相对误差较小，江宁台垂向观测于2018年4月25日至2018年11月22日曾采用该方法。考虑仅当电极埋深远大于供电极距时称为全空间，而江宁台垂向装置最小电极埋深仅与供电极距相当，因此，方法Ⅱ同样不适用于江宁台垂向观测。除江宁台外，大部分台站观测装置电极埋深明显小于供电极距，均不宜采用方法Ⅱ。方法Ⅲ相对误差最小，江宁台垂向地电阻率观测于2018年11月23日至2019年10月30日曾采用该方法，2018年11月出现的台阶是由调整装置系数导致的（图 4）。由于江宁台垂向地电阻率观测为多孔观测，须考虑井距才能准确计算其装置系数，因而最终采用方法Ⅳ进行计算。
$$ \sigma = \frac{{k_{方法}} - {k_{方法Ⅳ}}}{{{k_{方法Ⅳ}}}} $$ (16) 表 2 江宁台垂向观测的装置系数Table 2. The configuration coefficient of vertical geo-resistivity observation in Jiangning earthquake station计算方法 AM/m AN/m B1M/m B1N/m A1M/m A1N/m 装置系数K Ⅰ 75.000 125.000 675.000 725.000 — — 790.000 Ⅱ 75.000 125.000 — — — — 1178.000 Ⅲ 75.000 125.000 675.000 725.000 475.000 525.000 1167.000 Ⅳ 75.000 125.374 675.020 725.000 475.000 525.292 1162.000 
图 4 江宁台垂向观测整点值曲线Figure 4. The hourly observational value curves of vertical geo-resistivity observation at Jiangning Seismic Station5. 结论
本文以江宁台垂向地电阻率观测为例，提出2种以不完全全空间方式计算的新方法，并与现有垂向观测装置计算方法进行比较。研究结果表明，方法Ⅳ最符合江宁台垂向地电阻率观测装置。考虑方法Ⅳ中部分参数存在小数部分，认为保留小数点后三位能满足装置系数精度要求。方法Ⅳ除适用于2口井垂向观测装置外，同样适用于忽略井距时供电电极A埋深超过5m的单口井垂向观测装置。
致谢: 衷心感谢中国地震局地壳应力研究所王兰炜研究员对本文提出的建议和意见。 -
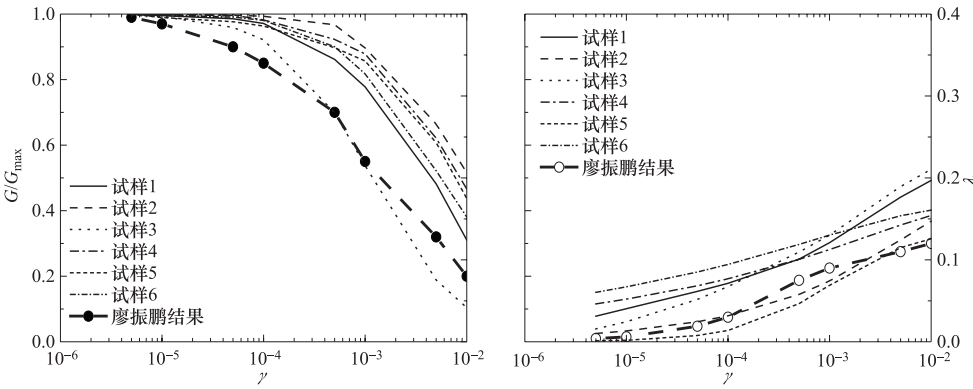
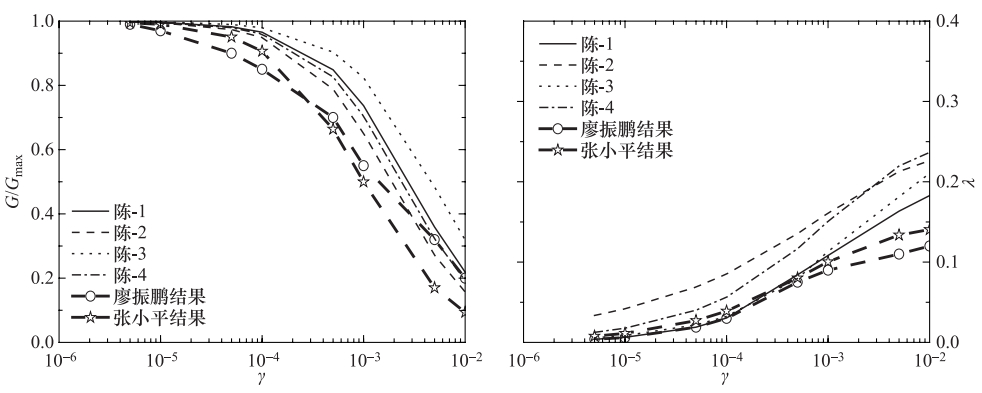
图 4 张小平等(2011)、陈党民等(2012)动三轴试验结果
Figure 4. Dynamic triaxial test results from Zhang Xiaoping et al.(2011) and Chen Dangmin et al.(2012)
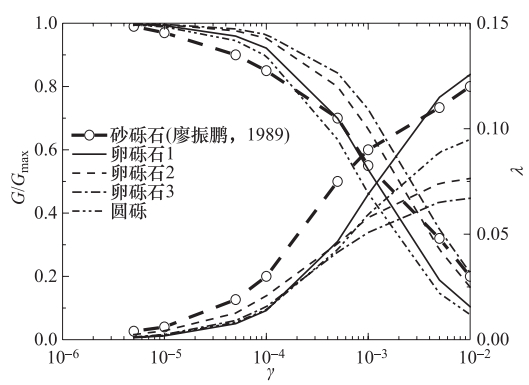
图 5 荣棉水等(2013)砂卵石动三轴试验结果
Figure 5. Dynamic triaxial test results of sandy pebbels from Rong Mianshui et al.(2013)
图 6 其他地震小区划卵砾石动三轴结果
Figure 6. Other dynamic triaxial test results of gravel from the seismic microzonation
图 7 砂卵(砾)石动三轴统计结果
Figure 7. The statistical results of the sand gravel dynamic triaxial test
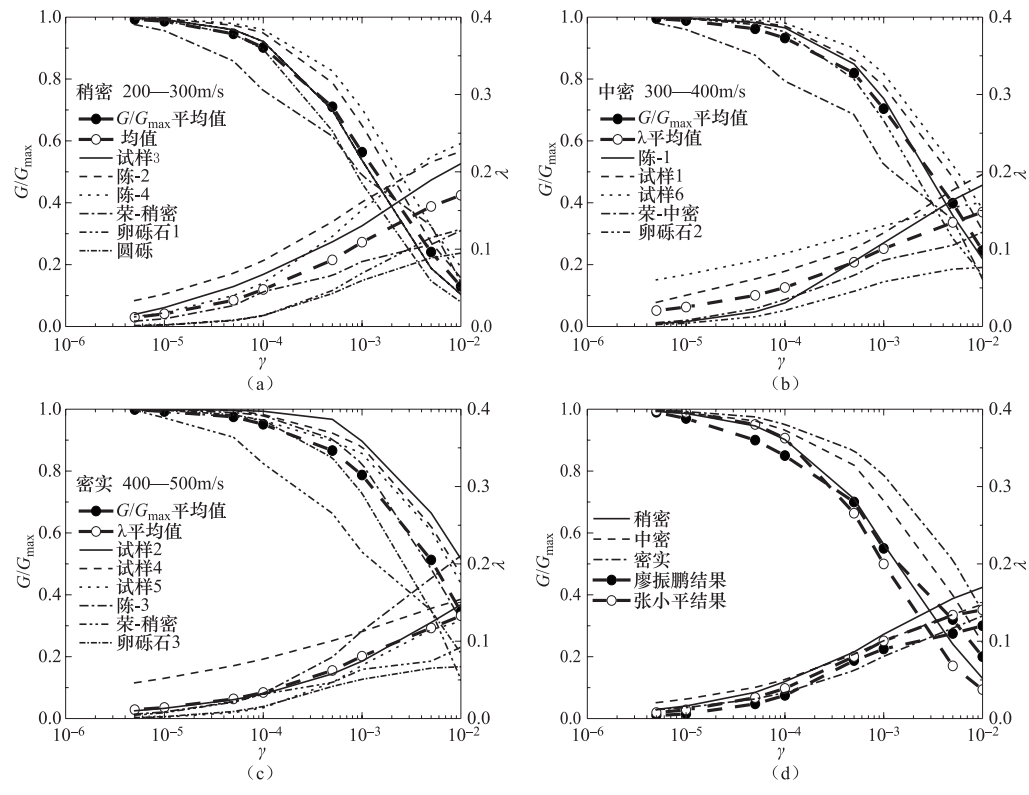
表 1 砂卵(砾)石动剪切模量比和阻尼比平均值及标准差
Table 1. The average and standard deviation of the dynamic shear modulus ratio and the damping ratio of the sand gravel
试样名称 量 剪应变γ 5×10-6 1×10-5 5×10-5 1×10-4 5×10-4 1×10-3 5×10-3 1×10-2 稍密
砂卵(砾)石
(200—300m/s)G/Gmax 0.9931 0.9866 0.9459 0.9017 0.7101 0.5633 0.2405 0.1299 标准差 0.0085 0.0152 0.0447 0.0716 0.0835 0.0944 0.0764 0.0417 λ 0.0118 0.0163 0.0339 0.0478 0.0861 0.109 0.1552 0.1697 标准差 0.0122 0.0153 0.0244 0.0288 0.0394 0.0438 0.0584 0.0616 中密
砂卵(砾)石
(300—400m/s)G/Gmax 0.9952 0.9889 0.9624 0.9326 0.8191 0.7041 0.3987 0.2456 标准差 0.0079 0.0161 0.0480 0.0787 0.0832 0.1158 0.0993 0.0975 λ 0.0206 0.0252 0.0403 0.0504 0.0831 0.1006 0.1346 0.1478 标准差 0.0253 0.0277 0.0314 0.0312 0.0287 0.0291 0.0433 0.0489 密实
砂卵(砾)石
(400—500m/s)G/Gmax 0.9988 0.9924 0.9751 0.951 0.8662 0.7871 0.5127 0.3461 标准差 0.0013 0.0107 0.0331 0.0632 0.1073 0.1356 0.1401 0.1543 λ 0.0115 0.0142 0.0254 0.0336 0.0621 0.0805 0.117 0.1328 标准差 0.0173 0.0189 0.0222 0.0228 0.0233 0.0262 0.0433 0.0505 
下载: 导出CSV
表 2 场地计算模型
Table 2. Calculation model of the site
序号 土性描述 层厚/m 剪切波速/m·s-1 密度/kg·m-3 动三轴序号 稍密 中密 密实 1 砂卵石 3.6 195 1930 1/2/3 4/5/6 7/8/9 2 砂卵石 4.2 251 1950 1/2/3 4/5/6 7/8/9 3 砂卵石 3.4 280 1980 1/2/3 4/5/6 7/8/9 4 砂卵石 3.8 330 2000 1/2/3 4/5/6 7/8/9 5 砂卵石 5.3 380 2100 1/2/3 4/5/6 7/8/9 6 砂卵石 4.5 420 2150 1/2/3 4/5/6 7/8/9 7 砂卵石 5.5 470 2200 1/2/3 4/5/6 7/8/9 8 计算基底 520 2300 11 11 11
下载: 导出CSV
表 3 不同超越概率下的水平向峰值加速度(单位：gal)
Table 3. Horizontal peak acceleration at different levels of exceeding probability (unit: gal)
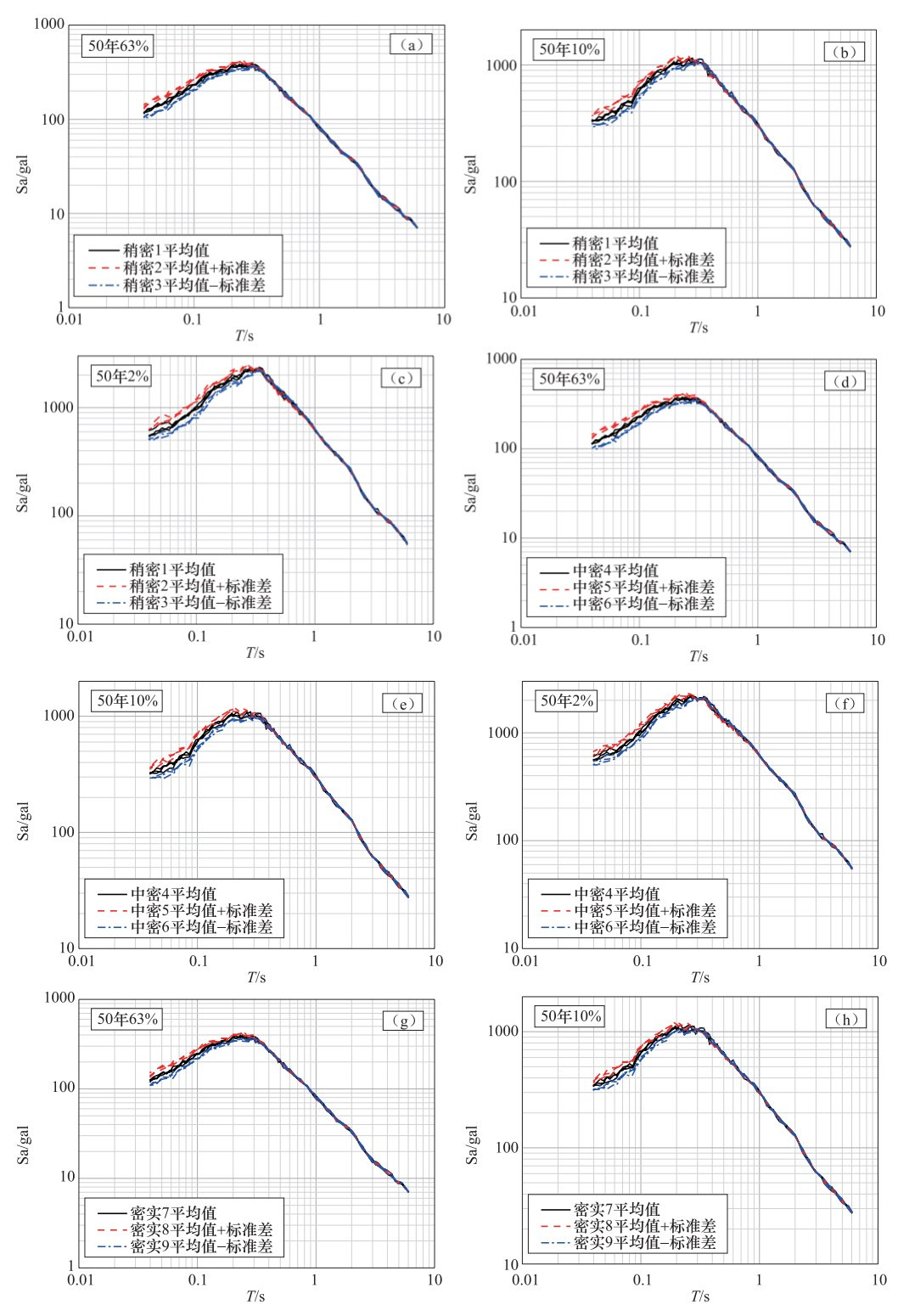
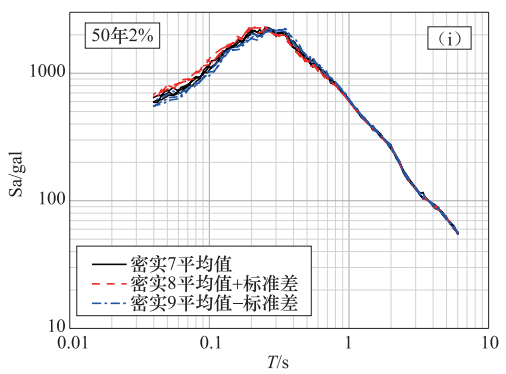
概率水平 50年63% 50年10% 50年2% 动三轴分类 稍密1 稍密2 稍密3 稍密1 稍密2 稍密3 稍密1 稍密2 稍密3 样本1 104.2 113.7 95.7 302.8 325.5 294.6 527.8 572.5 490.8 样本2 103.6 112.5 95.8 308.2 323.9 285.8 530.1 596.8 496.0 样本3 108.8 117.8 100.0 303.3 332.5 279.3 551.5 620.6 523.3 平均值 106 115 97 305 327 287 536 597 503 比例 1.0 1.09 0.92 1.0 1.07 0.94 1.0 1.14 0.94 动三轴分类 中密4 中密5 中密6 中密4 中密5 中密6 中密4 中密5 中密6 样本1 101.8 113.8 92.6 294.6 319.2 282.0 517.4 557.6 490.7 样本2 101.6 112.6 92.9 292.9 312.8 273.4 531.0 575.1 486.6 样本3 107.0 118.0 97.3 295.0 326.5 269.1 550.7 602.8 515.1 平均值 103 115 94 294 320 275 533 579 497 比例 1.0 1.12 0.91 1.0 1.09 0.93 1.0 1.09 0.94 动三轴分类 密实7 密实8 密实9 密实7 密实8 密实9 密实7 密实8 密实9 样本1 107.5 116.2 99.3 308.6 328.5 292.4 541.1 563.7 524.8 样本2 106.6 115.4 99.5 307.6 320.1 292.2 554.0 585.4 528.6 样本3 112.1 120.2 104.5 314.9 336.6 287.5 579.8 613.0 552.4 平均值 109 117 101 310 328 291 558 587 535 比例 1.0 1.08 0.92 1.0 1.06 0.93 1.0 1.06 0.95
下载: 导出CSV
-
陈党民, 田伟新, 段蕊, 2012.西安地区典型土动剪切模量比和阻尼比的统计研究.世界地震工程, 28(3):136-142. http://www.cnki.com.cn/Article/CJFDTOTAL-SJDC201203026.htm 陈国兴, 刘雪珠, 2004.南京及邻近地区新近沉积土的动剪切模量和阻尼比的试验研究.岩石力学与工程学报, 23(8):1403-1410. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=yslxygcxb200408033 陈国兴, 刘雪珠, 王炳辉, 2007.土动力参数变异性对深软场地地表地震动参数的影响.防灾减灾工程学报, 27(1):1-10. http://d.wanfangdata.com.cn/Periodical_dzxk200701001.aspx 国家质量技术监督局, 中华人民共和国建设部, 1999. GB/T 50123-1999土工试验方法标准[2007版]. 北京: 中国计划出版社. 贺为民, 李德庆, 杨杰等, 2016.土的动剪切模量、阻尼比和泊松比研究进展.地震工程学报, 38(2):309-317. doi: 10.3969/j.issn.1000-0844.2016.02.0309 孔宇阳, 廉超, 李井冈, 2014.武汉地区典型土类动力非线性参数的统计分析.地震工程学报, 36(4):832-837. http://xueshu.baidu.com/s?wd=paperuri%3A%28b9b26f20e5981d5b10864f3bee4ea089%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fkns.cnki.net%2FKCMS%2Fdetail%2Fdetail.aspx%3Ffilename%3Dzbdz201404011%26dbname%3DCJFD%26dbcode%3DCJFQ&ie=utf-8&sc_us=15851087737565078771 李建有, 太树刚, 林凤仙等, 2015.昆明盆地粉质粘土土动力参数研究.震灾防御技术, 10(4):872-883. doi: 10.11899/zzfy20150405 廖振鹏, 1989.地震小区划——理论与实践.北京:地震出版社. 吕悦军, 唐荣余, 沙海军, 2003.渤海海底土类动剪切模量比和阻尼比试验研究.防灾减灾工程学报, 23(2):35-42. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGEM201206001152.htm 荣棉水, 王世元, 李小军等, 2013.成都盆地不同工程地质分区内场地地震动参数的计算分析.地震学报, 35(4):543-552. https://www.researchgate.net/profile/Xiaojun_Li5/publication/295458414_Calculation_and_analysis_of_seismic_ground_motion_parameters_for_different_engineering_geological_divisions_of_Chengdu_basin/links/5800ad1e08ae181e57828faa.pdf?origin=publication_detail 陕西省工程地震勘察研究院, 2016. 商洛市地震小区划报告. 西安: 陕西省工程地震勘察研究院. 史丙新, 周荣军, 吕悦军等, 2015.成都平原粘性土动力学参数统计分析.震灾防御技术, 10(2):305-315. doi: 10.11899/zzfy20150210 施春花, 吕悦军, 彭艳菊等, 2009.北京地区粉质粘土土动力学参数的统计分析.震灾防御技术, 4(1):69-79. doi: 10.11899/zzfy20090107 孙静, 袁晓铭, 2003.土的动模量和阻尼比研究述评.世界地震工程, 19(1):88-95. http://www.cqvip.com/qk/93082x/2003001/7566188.html 孙锐, 陈红娟, 袁晓铭, 2010.土的非线性动剪切模量比和阻尼比不确定性分析.岩土工程学报, 32(8):1228-1235. https://www.wenkuxiazai.com/doc/0a03ef97b0717fd5370cdc31-2.html 王绍博, 丁海平, 2001.土动力参数对土层动力反应的影响.地震工程与工程振动, 21(1):105-108. http://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200101019.htm 新疆防御自然灾害研究所, 2015a. 和田市城市地震小区划报告. 乌鲁木齐: 新疆防御自然灾害研究所. 新疆防御自然灾害研究所, 2015b. 新疆呼图壁县地震小区划报告. 乌鲁木齐: 新疆防御自然灾害研究所. 袁晓铭, 孙锐, 孙静等, 2000.常规土类动剪切模量比和阻尼比试验研究.地震工程与工程振动, 20(4):133-139. http://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200004021.htm 张小平, 牛雪, 赵安生等, 2011.大连地区场地土动力学参数初步研究.中国地震, 27(3):280-289. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgdz201103007 张亚军, 兰宏亮, 崔永高, 2010.上海地区土动剪切模量比和阻尼比的统计研究.世界地震工程, 26(2):171-175. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sjdzgc201002031 中国地震局, 1994.DB 001-94工程场地地震安全性评价工作规范.北京:地震出版社. 中国地震灾害防御中心, 2015. 喀什经济开发区地震小区划及活断层探测工程(地震小区划部分). 北京: 中国地震灾害防御中心. 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会, 2005.GB 17741-2005工程场地地震安全性评价.北京:中国标准出版社. -
下载:
点击查看大图
计量
- 文章访问数: 160
- HTML全文浏览量: 57
- PDF下载量: 26
- 被引次数: 0
