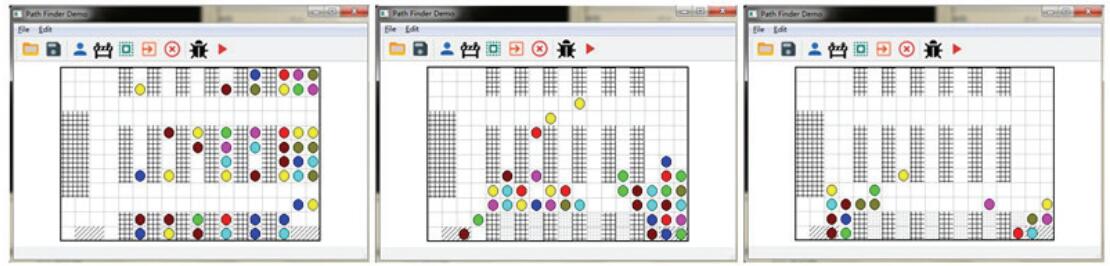
The Evacuation Model of Evacuating the Drill Personnel in Primary and Secondary School
-
摘要: 本文以元胞自动机模型理论为指导，以人员疏散时间最短为目标，构建中小学校疏散演练人员疏散模型。本文从开展地震应急疏散模型研究出发，为地震应急演练疏散训练软件提供核心算法。通过对空间基础构建元素及搭建方法的分析研究，设计完成疏散虚拟场景的建模方法。最后开展人员疏散算法构建方式的研究，并结合应急疏散演练人员行为规范的研究成果，完成疏散模型的总体设计，达到为应急演练疏散软件提供人员疏散演化模型以及为人员疏散过程合理性评判提供依据的目的。
-
关键词:
- 地震应急疏散模型 /
- 元胞自动机 /
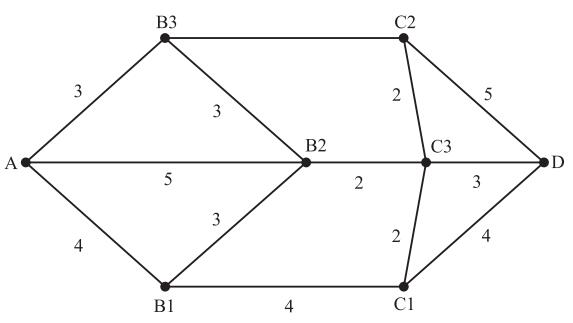
- Dijkstra算法 /
- 递推 /
- 疏散策略
Abstract: On the basis of cellular automata models, we build the evacuation model of evacuating the drill personnel in primary and secondary school with the aim of shortest evacuation time. This model provides the core algorithm for earthquake emergency training evacuation training software. Through analysis of spatial foundation construction elements and construction methods, we design the virtual scene modeling method. We also construct a method of personnel evacuation algorithm and combine the research results of emergency evacuation practice personnel to complete the overall design of evacuation model. The model provides the basis for judging the rationality of personnel evacuation process in practise. -
图 1 疏散场景模型的搭建流程
Figure 1. The flow chart of the establishment of evacuation scenario model
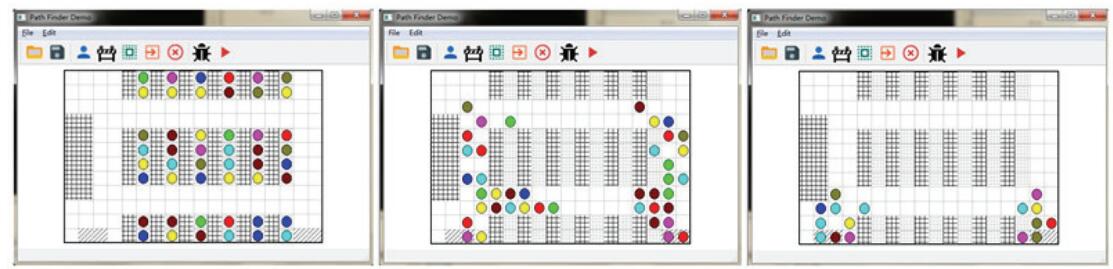
表 1 不同版本疏散完成数据的对比
Table 1. The comparison results of different forms of evacuation
版本及人员分布分类 左边出口疏散完成人数 右边出口疏散完成人数 疏散完成所用步数 未优化版本的人员均匀分布 22 26 26 未优化版本的人员不均匀分布 10 38 35 优化版本的人员均匀分布 23 25 24 优化版本的人员不均匀分布 21 27 29 
下载: 导出CSV
-
刘欢, 2013. 建筑物内人员疏散算法与仿真. 上海: 复旦大学. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2702944 岳昊, 邵春福, 关宏志等, 2010.基于元胞自动机的行人视线受影响的疏散流仿真研究.物理学报, 59(7):4499-4507. doi: 10.7498/aps.59.4499 张福浩, 刘纪平, 李青元, 2004.基于Dijkstra算法的一种最短路径优化算法.遥感信息, (2):38-41. doi: 10.3969/j.issn.1000-3177.2004.02.011 张培红, 2002. 建筑物火灾时人员疏散行为的研究. 沈阳: 东北大学. http://d.wanfangdata.com.cn/Thesis/Y495665 张树平, 2004. 建筑火灾中人的行为反应研究. 西安: 西安建筑科技大学. http://d.wanfangdata.com.cn/Thesis/Y616550 Burstedde C., Klauck K., Schadschneider A., et al., 2001. Simulation of pedestrian dynamics using a two-dimensional cellular automaton. Physica A:Statistical Mechanics and its Applications, 295(3-4):507-525. doi: 10.1016/S0378-4371(01)00141-8 Dijkstra E. W., 1959. A note on two problems in connection with graphs. Numerische Mathematik, 1:269-271. doi: 10.1007/BF01386390 Kirchner A., Schadschneider A., 2002. Simulation of evacuation processes using a bionics-inspired cellular automaton model for pedestrian dynamics. Physica A:Statistical Mechanics and its Applications, 312(1-2):260-276. doi: 10.1016/S0378-4371(02)00857-9 Pauls J. L., 1978. "Evacuation of high rise office buildings." Buildings, 72(5):84-88. https://www.sciencedirect.com/science/article/pii/0379711283900206 Yang L. Z., Fang W. F., Huang R., et al., 2002. Occupant evacuation model based on cellular automata in fire. Chinese Science Bulletin, 47(17):1484-1488. doi: 10.1360/02tb9327 -
点击查看大图
图(8) / 表(1)
计量
- 文章访问数: 66
- HTML全文浏览量: 40
- PDF下载量: 0
- 被引次数: 0
