Seismic Performance Evaluation of RC Frames with Different Seismic Precautionary Intensity Based on Vulnerability Analysis
-
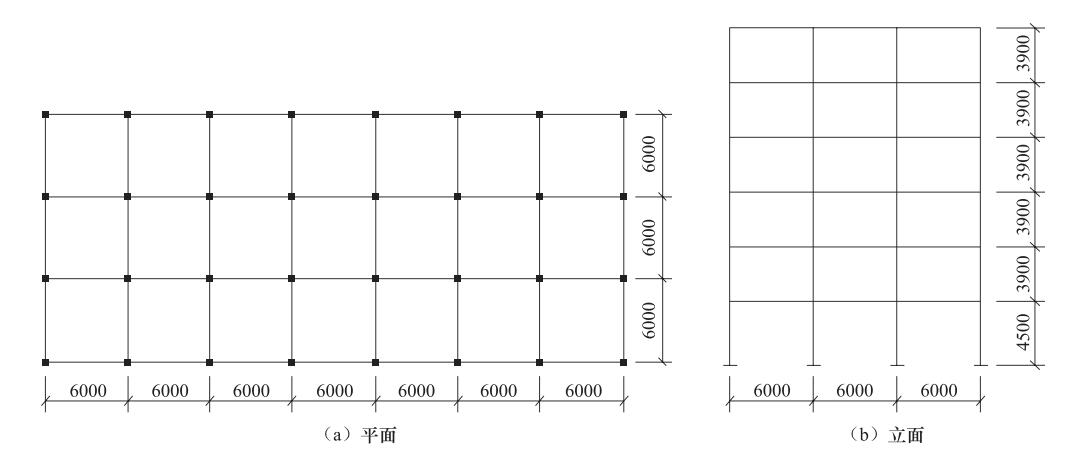
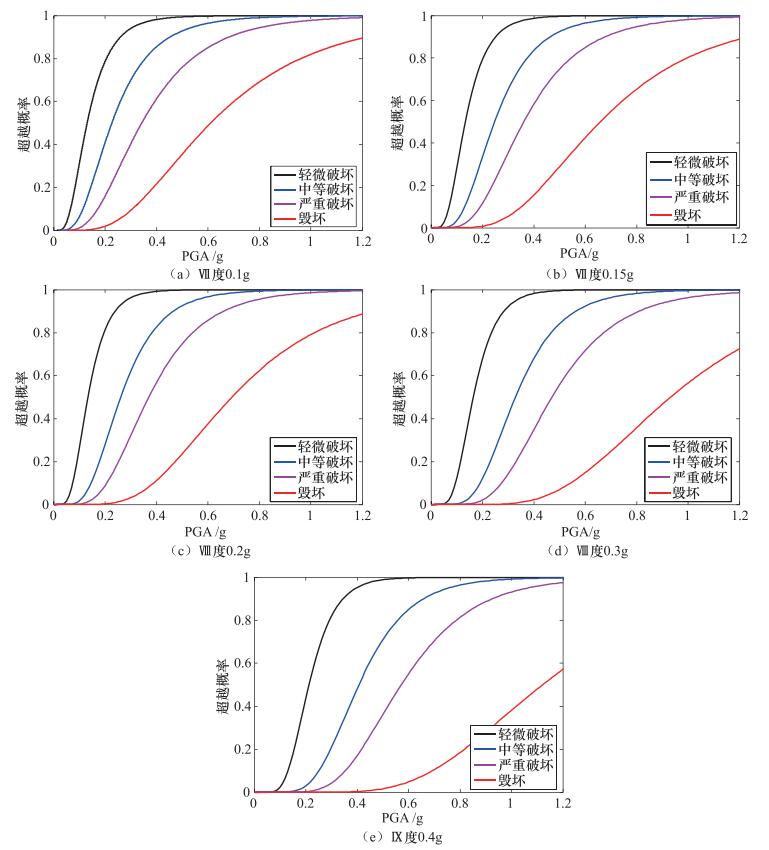
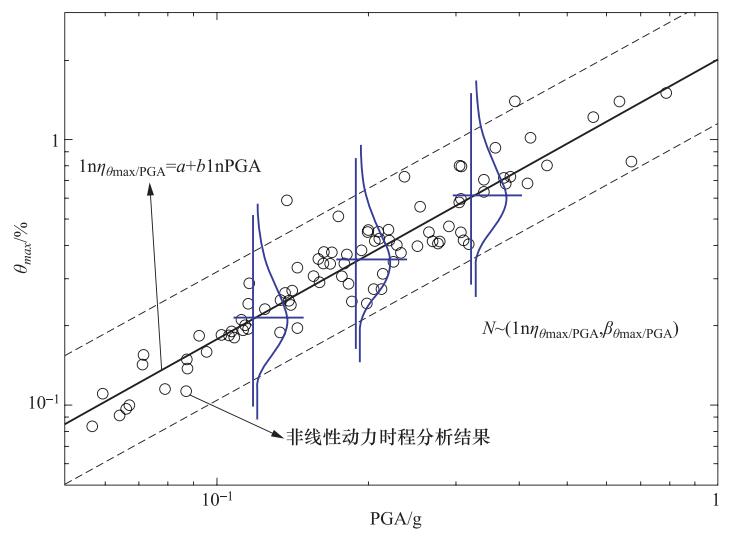
摘要: 借助非线性动力时程分析，对严格按照规范Ⅶ、Ⅷ、Ⅸ度设计的5个三跨6层钢筋混凝土框架结构开展易损性分析，建立了基于峰值加速度的易损性曲线。从易损性的角度对不同设防标准RC框架结构的抗震性能做了定量评价，并探讨了设防标准对RC框架结构易损性的影响。分析表明，对应于设防小震、中震及大震水平的峰值加速度，结构“小震不坏”、“中震可修”和“大震不倒”的失效概率均在18%以内，可认为结构满足三水准的性态控制目标。随着结构设防标准的提高，其易损性随之降低，相同峰值加速度对应的各个破坏状态的超越概率均有所降低。此外，将框架结构的设防烈度提高1度，其“大震不倒”的失效概率会明显减小。而将框架结构的设防烈度降低1度，其“大震不倒”的失效概率会显著增加，最高可达4倍。Abstract: Five RC frames of three-span and six-story were designed with seismic precautionary intensities of Ⅶ、Ⅷ and Ⅸ degree. Vulnerability analysis of the five frames was performed by means of nonlinear dynamic time history analysis. Vulnerability curves based on peak ground acceleration were developed. Seismic performance of the five RC frames was quantitatively evaluated at the point of vulnerability. The effect of fortification criterion on vulnerability was discussed. It shows that, when meeting peak ground acceleration corresponding to small, moderate and large earthquake levels, the failure probabilities of "Undamaged under small earthquake", "Repairable under moderate earthquake" and "No-collapsing under large earthquake" are less than 18%, which satisfies the three level seismic performance targets. With the increase of seismic precautionary intensity, the exceedance probability of each damage state corresponding to a given peak ground acceleration is reduced. In addition, with increasing one degree of the seismic precautionary intensity, the failure probability of "No-collapsing under large earthquake" decreases. With reducing one degree of the seismic precautionary intensity, the failure probability of "No-collapsing under large earthquake" increases significantly, even up to four times.
-
图 3 不同设防标准框架结构基于峰值加速度的易损性曲线
Figure 3. PGA based vulnerability curves of RC frames with different seismic precautionary intensity
图 4 不同设防标准框架结构易损性曲线的比较
Figure 4. Comparison of vulnerability curves of RC frames with different seismic precautionary intensity
表 1 不同破坏状态对应最大层间位移角的统计参数
Table 1. Statistic parameters of θmax for different damage states
破坏状态 轻微破坏 中等破坏 严重破坏 毁坏 层间位移角均值（$ {\mu _{{\theta _{\max }}/{\rm{DS}}}}$） 1/350（0.00286） 1.10θy 1/80（0.0125） 1.11θu 变异系数（$ {\delta _{{\theta _{\max }}/{\rm{DS}}}}$） 0.38 0.38 0.38 0.38 
下载: 导出CSV
表 2 输入地震动记录的基本信息
Table 2. Basic details of input ground motion records
地震事件 发生年 台站名 MW Rrup/km Vs30/m·s-1 PGA/g PGV/cm·s-1 Imperial Valley-06 1979 Calipatria Fire Station 6.53 24.6 205.8 0.078 13.3 Imperial Valley-06 1979 Chihuahua 6.53 7.3 274.5 0.27 12.422 Imperial Valley-06 1979 Compuertas 6.53 15.3 274.5 0.186 6.913 Imperial Valley-06 1979 El Centro Array #1 6.53 21.7 237.3 0.14 15.844 Imperial Valley-06 1979 El Centro Array #12 6.53 17.9 196.9 0.116 21.809 Imperial Valley-06 1979 El Centro Array #13 6.53 22 249.9 0.139 12.978 Imperial Valley-06 1979 Niland Fire Station 6.53 36.9 207.5 0.109 11.872 Imperial Valley-06 1979 Plaster City 6.53 30.3 345.4 0.111 17.794 Imperial Valley-06 1979 Parachute Test Site 6.53 12.7 348.7 0.057 5.388 Imperial Valley-06 1979 Westmorland Fire Sta 6.53 15.2 193.7 0.11 21.891 Loma Prieta 1989 Agnews State Hospital 6.93 24.6 239.7 0.172 25.94 Loma Prieta 1989 Capitola 6.93 15.2 288.6 0.443 29.217 Loma Prieta 1989 Coyote Lake Dam (Downst) 6.93 20.8 295 0.16 13.039 Loma Prieta 1989 Gilroy Array #3 6.93 12.8 349.9 0.367 44.665 Loma Prieta 1989 Gilroy Array #4 6.93 14.3 221.8 0.212 37.861 Loma Prieta 1989 Gilroy Array #7 6.93 22.7 333.9 0.226 16.404 Loma Prieta 1989 Halls Valley 6.93 30.5 281.6 0.134 15.403 Loma Prieta 1989 Hollister Diff. Array 6.93 24.8 215.5 0.279 35.569 Loma Prieta 1989 Palo Alto -SLAC Lab 6.93 30.9 425.3 0.194 37.448 Loma Prieta 1989 Salinas -John & Work 6.93 32.8 271.4 0.112 15.68 Loma Prieta 1989 Sunnyvale -Colton Ave. 6.93 24.2 267.7 0.207 37.278 Northridge-01 1994 Arcadia -Arcadia Av 6.69 39.7 308.6 0.104 7.316 Northridge-02 1994 Baldwin Park -N Holly 6.69 48 308.6 0.123 8.17 Northridge-03 1994 Canoga Park -Topanga Can 6.69 14.7 267.5 0.42 60.688 Northridge-04 1994 Downey – Birchdale 6.69 48.9 245.1 0.171 8.126 Northridge-05 1994 Elizabeth Lake 6.69 36.5 234.9 0.109 8.961 Northridge-06 1994 Glendale -Las Palmas 6.69 22.2 446 0.206 7.386 Northridge-07 1994 LA -Centinela St 6.69 28.3 234.9 0.322 22.866 Northridge-08 1994 LA -Fletcher Dr 6.69 27.3 446 0.24 26.219 Northridge-09 1994 LA -N Faring Rd 6.69 20.8 405.2 0.273 15.805 Northridge-10 1994 LA -Pico & Sentous 6.69 31.3 270.2 0.186 14.234 Northridge-11 1994 LA -Saturn St 6.69 27 308.7 0.475 34.478 Northridge-12 1994 LA -Univ. Hospital 6.69 34.2 376.1 0.214 10.76 Northridge-13 1994 La Crescenta -New York 6.69 18.5 446 0.159 11.276 Northridge-14 1994 Lawndale -Osage Ave 6.69 39.9 361.2 0.153 7.953 San Fernando 1971 LA -Hollywood Stor FF 6.61 22.8 316.5 0.174 14.849 Superstitn Hills 1987 Brawley Airport 6.54 17 208.7 0.156 13.896 Superstitn Hills 1987 Calipatria Fire Station 6.54 27 205.8 0.247 14.544 Superstitn Hills 1987 Plaster City 6.54 22.2 345.4 0.186 20.619 Superstitn Hills 1987 Poe Road (temp) 6.54 11.2 207.5 0.446 35.711 Mammoth Lakes-03 1980 Convict Creek 5.91 12.5 338.5 0.233 20.87 Coalinga-05 1983 Oil Fields Fire Station-Pad 5.77 11.1 376.1 0.228 19.228 Coalinga-05 1983 Oil Fields Fire Station-Pad 5.77 11.1 376.1 0.228 19.228 Coalinga-05 1983 Oil Fields Fire Station-FF 5.77 11.1 376.1 0.224 15.186 Coyote Lake 1979 Gilroy Array #2 5.74 9 270.8 0.154 12.307 Coalinga-05 1983 Skunk Hollow 5.77 11 376.1 0.376 16.287 N. Palm Springs 1986 Cabazon 6.06 11.8 345.4 0.231 6.732 Chalfant Valley-01 1986 Zack Brothers Ranch 5.77 6.4 271.4 0.219 19.829 Coalinga-05 1983 Palmer Ave 5.77 12.3 376.1 0.271 13.581 Morgan Hill 1984 Halls Valley 6.19 3.5 281.6 0.314 39.555 Coyote Lake 1979 Gilroy Array #3 5.74 7.4 349.9 0.251 18.407 Mammoth Lakes-02 1980 Convict Creek 5.69 9.5 338.5 0.178 12.168 Mammoth Lakes-06 1980 Convict Creek 5.94 12.2 338.5 0.299 16.084 Mammoth Lakes-03 1980 Long Valley Dam (Upr L Abut) 5.91 18.1 345.4 0.184 10.932 Whittier Narrows-01 1987 Pasadena -CIT Calif Blvd 5.99 17.3 370.8 0.286 14.891 Mammoth Lakes-01 1980 Mammoth Lakes H. S. 6.06 4.7 370.8 0.227 9.796 Whittier Narrows-01 1987 Pasadena-Brown Gym 5.99 17.3 370.8 0.156 12.408 Whittier Narrows-01 1987 Whittier Narrows Dam upstream 5.99 14.7 298.7 0.293 14.33 N. Palm Springs 1986 Desert Hot Springs 6.06 6.8 345.4 0.329 26.931 Whittier Narrows-01 1987 Pasadena-CIT Indust. Rel 5.99 17.3 370.8 0.235 13.181 Whittier Narrows-01 1987 San Marino-SW Academy 5.99 15.9 379.4 0.201 12.585 Coalinga-05 1983 Burnett Construction 5.77 11.5 352.2 0.268 13.665 Whittier Narrows-01 1987 Pasadena-CIT Lura St 5.99 17.3 370.8 0.32 17.333 Mammoth Lakes-02 1980 Mammoth Lakes H. S. 5.69 9.1 370.8 0.421 25.405 Kocaeli-Turkey 1999 Goynuk 7.51 31.7 424.8 0.132 9.512 Kocaeli-Turkey 1999 Iznik 7.51 30.7 274.5 0.098 15.338 Chi-Chi-Taiwan 1999 CHY050 7.62 44.8 432.9 0.098 9.458 Chi-Chi-Taiwan 1999 CHY088 7.62 37.5 366.2 0.145 16.995 Chi-Chi-Taiwan 1999 HWA011 7.62 53.2 241.7 0.092 22.133 Chi-Chi-Taiwan 1999 HWA015 7.62 51.1 334.6 0.108 12.907 Chi-Chi-Taiwan 1999 HWA016 7.62 52.2 344 0.096 10.994 Chi-Chi-Taiwan 1999 HWA027 7.62 51.6 282.9 0.1 13.502 Chi-Chi-Taiwan 1999 HWA028 7.62 53.8 241.7 0.123 18.227 Chi-Chi-Taiwan 1999 HWA031 7.62 51.5 473 0.094 21.591 Chi-Chi-Taiwan 1999 HWA033 7.62 53.2 395.6 0.167 16.93 Chi-Chi-Taiwan 1999 HWA034 7.62 44.3 379.2 0.133 12.019 Chi-Chi-Taiwan 1999 HWA037 7.62 46.2 476.9 0.108 13.64 Chi-Chi-Taiwan 1999 HWA059 7.62 49.1 421.6 0.139 16.403 Chi-Chi-Taiwan 1999 TCU015 7.62 49.8 426 0.118 36.352 Chi-Chi-Taiwan 1999 TCU033 7.62 40.9 423.4 0.19 37.92 Chi-Chi-Taiwan 1999 TCU034 7.62 35.7 393.8 0.231 43.03 Chi-Chi-Taiwan 1999 TCU098 7.62 47.7 229.7 0.107 32.349 Chi-Chi-Taiwan 1999 TCU113 7.62 31.1 230.3 0.07 26.891 Imperial Valley-06 1979 Calexico Fire Station 6.53 10.4 231.2 0.263 21.203 Loma Prieta 1989 Gilroy Array #4 6.93 14.3 221.8 0.345 35.751 Northridge-01 1994 LA-Wadsworth VA Hospital South 6.69 23.6 413.8 0.419 38.356 Coalinga-01 1983 Pleasant Valley P.P.-yard 6.36 8.4 257.4 0.59 60.061 Loma Prieta 1989 Gilroy-Historic Bldg. 6.93 11 338.5 0.254 21.899 Northridge-01 1994 LA-Brentwood VA Hospital 6.69 22.5 416.6 0.188 18.137 Chi-Chi-Taiwan-06 1999 TCU072 6.3 13 468.1 0.077 9.332 Imperial Valley-06 1979 Parachute Test Site 6.53 12.7 348.7 0.135 16.573
下载: 导出CSV
表 3 小震、中震及大震对应的峰值加速度（单位：g）
Table 3. PGA values corresponding to small, moderate and large earthquake (unit: g)
Ⅶ度0.1g Ⅶ度0.15g Ⅷ度0.2g Ⅷ度0.3g Ⅸ度0.4g 小震 0.036 0.054 0.072 0.108 0.144 中震 0.1 0.15 0.2 0.3 0.4 大震 0.225 0.324 0.405 0.54 0.756
下载: 导出CSV
表 4 小震、中震及大震水准地震作用下结构各个破坏状态的超越概率
Table 4. Exceeding probability of different damage states under small, moderate and large earthquake
设防标准 地震作用水准 峰值加速度/g 超越概率 轻微破坏 中等破坏 严重破坏 毁坏 Ⅶ（0.1g） 小震 0.036 0.96 0.03 0 0 中震 0.1 33.06 6.45 1.04 0.03 大震 0.225 86.8 51.5 22.56 3.07 Ⅶ（0.15g） 小震 0.054 3.36 0.11 0.01 0 中震 0.15 59.03 15.4 3.69 0.13 大震 0.324 96.37 70.83 41.31 7.42 Ⅷ（0.2g） 小震 0.072 8.66 0.24 0.02 0 中震 0.2 81.26 27.88 8.74 0.3 大震 0.405 99.27 83.42 57.96 11.75 Ⅷ（0.3g） 小震 0.108 15.86 0.43 0.03 0 中震 0.3 92.18 41.54 14.25 0.36 大震 0.54 99.75 88.08 62.68 9.77 Ⅸ（0.4g） 小震 0.144 15.1 0.3 0.01 0 中震 0.4 95.37 48.33 17.13 0.31 大震 0.756 99.96 95.06 77.14 14.75
下载: 导出CSV
表 5 结构三水准性态控制目标的失效概率
Table 5. Failure probabilities of the three performance targets
失效概率/% Ⅶ度0.1g Ⅶ度0.15g Ⅷ度0.2g Ⅷ度0.3g Ⅸ度0.4g 小震不坏 0.96 3.36 8.66 15.86 15.1 中震可修 1.04 3.69 8.74 14.25 17.13 大震不倒 3.07 7.42 11.75 9.77 14.75
下载: 导出CSV
表 6 大震峰值加速度对应的结构的倒塌概率（%）
Table 6. Collapse probability of RC frames corresponding to PGA (%) of large earthquake
Ⅶ—Ⅸ度大震水准下对应的峰值加速度/g 0.225 0.324 0.405 0.5 0.756 Ⅶ（0.1g） 3.07 12.07 22.87 42.42 67.53 Ⅶ（0.15g） 1.44 7.42 16.08 34.26 61.02 Ⅷ（0.2g） 0.65 4.65 11.75 29.03 57.55 Ⅷ（0.3g） 0.04 0.61 2.41 9.76 30.93 Ⅸ（0.4g） 0 0.05 0.34 2.6 14.75
下载: 导出CSV
-
高小旺, 沈聚敏, 1993a."大震"作用下钢筋混凝土框架房屋变形能力的抗震可靠度分析.土木工程学报, 26(3):3-12. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=tmgc199303000&dbname=CJFD&dbcode=CJFQ 高小旺, 沈聚敏, 1993b.钢筋混凝土框架房屋不同破坏状态的抗震可靠度分析.建筑科学, 9(1):3-11. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=jzkx199301001&dbname=CJFD&dbcode=CJFQ 高小旺, 沈聚敏, 1993c.钢筋砼框架结构层间极限变形能力的简化计算方法.建筑结构学报, 14(2):28-38. http://mall.cnki.net/magazine/Article/JCJG200712008.htm 高小旺, 邵卓民, 1996. 钢筋混凝土房屋变形能力的抗震可靠度分析. "灾害作用和结构抗灾可靠度标准研究"一九九六年度研究报告. 中国建筑科学研究院工程抗震研究所, 建设部标准定额研究所. 王振波, 解子林, 2015.现浇板对RC框架结构抗震性能影响的试验研究.震灾防御技术, 10(4):979-985. doi: 10.11899/zzfy20150416 吴勇, 雷汲川, 杨红等, 2002.板筋参与梁端负弯矩承载力问题的探讨.重庆建筑大学学报, 24(3):33-37. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=jian200203007&dbname=CJFD&dbcode=CJFQ 尹之潜, 1995.地震灾害及损失预测方法.北京:地震出版社. 中国建筑科学研究院, 2010. 建筑抗震设计规范(GB 50011-2010). 北京: 中国建筑工业出版社. 钟益村, 王文基, 田家骅, 1984.钢筋混凝土结构房屋变形性能及容许变形指标.建筑结构, (2):38-45. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=jcjg198402009&dbname=CJFD&dbcode=CJFQ PEER ground motion database. http://peer.berkeley.edu/nga. Prakash V., Powell G. H., Campbell S., 1993. DRAIN-2DX: basic program description and user guide. Report No. UBC/SEMM-93/17. Berkeley: University of California at Berkeley. Shinozuka M., Feng M. Q., Lee J, et al., 2000. Statistical analysis of fragility curves. Journal of Engineering Mechanics, 126(12):1224-1234. doi: 10.1061/(ASCE)0733-9399(2000)126:12(1224) Shome N., 1999. Probabilistic seismic demand analysis of nonlinear structures. Stanford: Stanford University. http://dl.acm.org/citation.cfm?id=928965 Singhal A., Kiremidjian A. S., 1996. Method for probabilistic evaluation of seismic structural damage. Journal of Structural Engineering, 122(12):1459-1467. doi: 10.1061/(ASCE)0733-9445(1996)122:12(1459) Song J. L., Ellingwood B. R., 1999. Probabilistic modeling of steel moment frames with welded connections. Engineering Journal (AISC), 36(3):129-137. https://www.researchgate.net/publication/286974260_Probabilistic_modeling_of_steel_moment_frames_with_welded_connections -
点击查看大图
图(4) / 表(6)
计量
- 文章访问数: 111
- HTML全文浏览量: 51
- PDF下载量: 9
- 被引次数: 0
