Preliminary Analysis of Distribution Characteristics of Ground Motion and Attenuation Relation of the Jiuzhaigou MS7.0 Earthquake on August 24, 2016, Sichuan, China
-
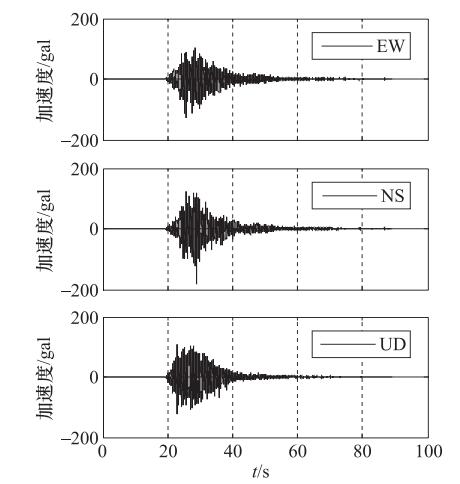
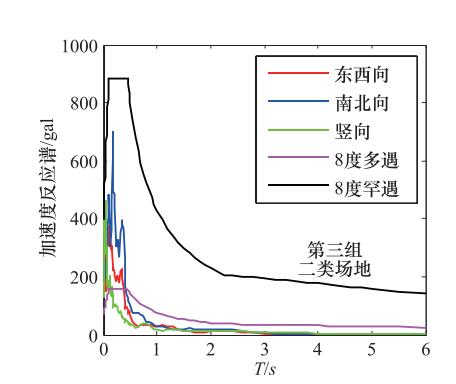
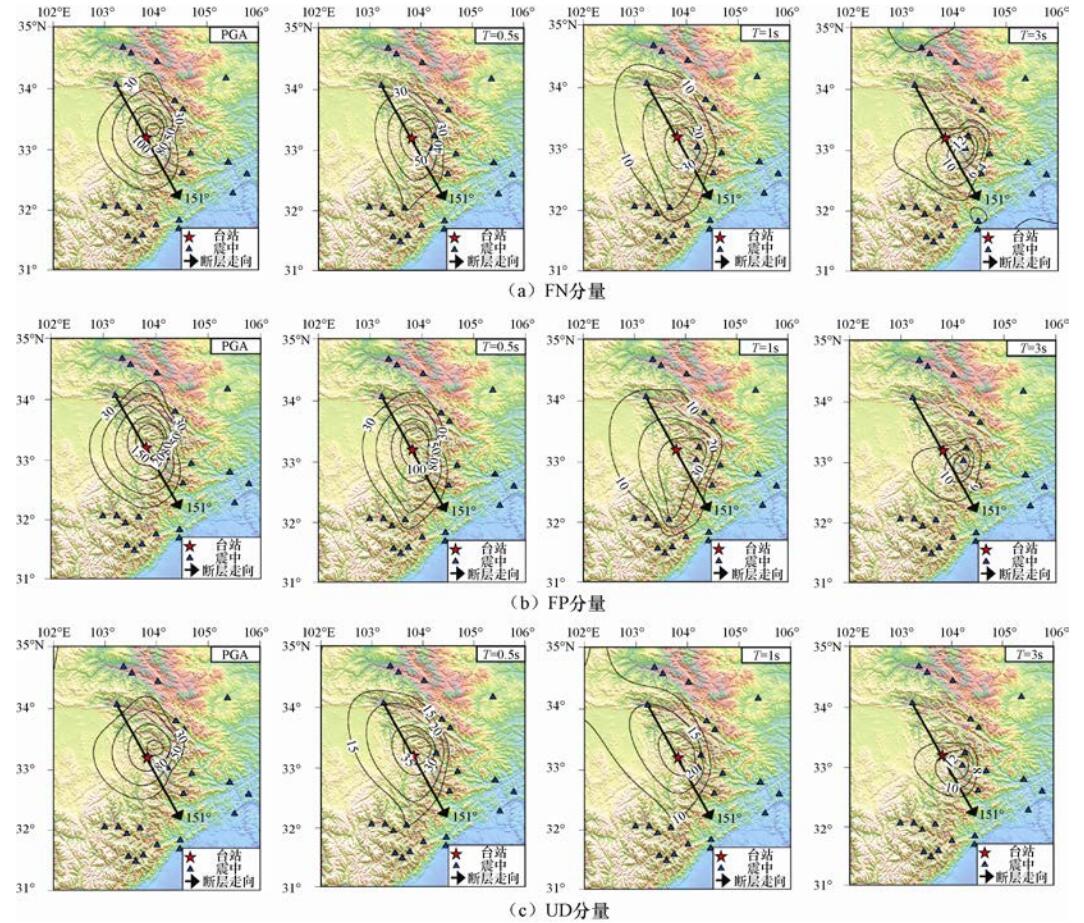
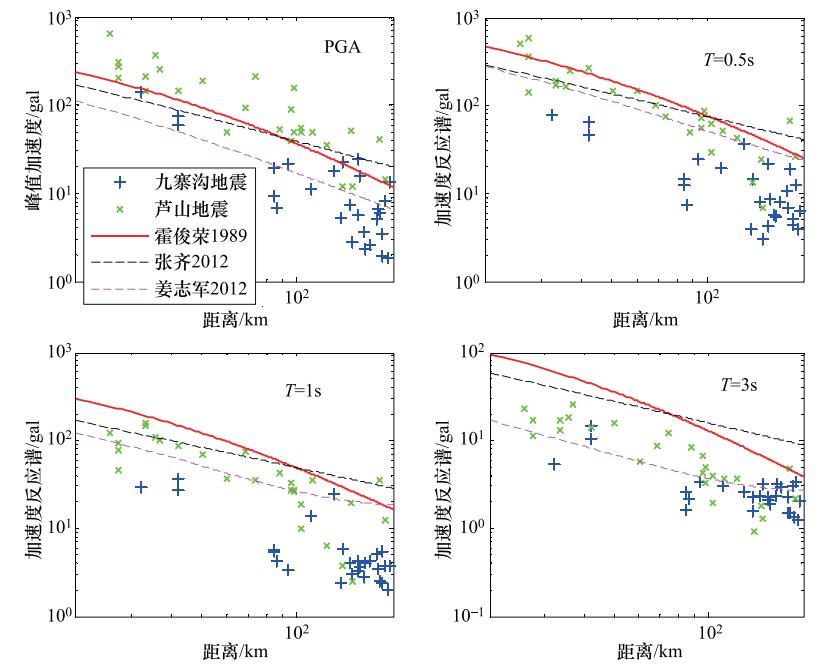
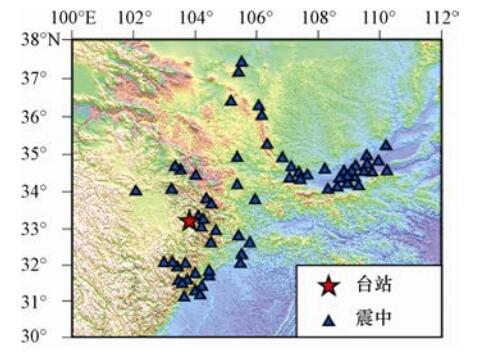
摘要: 2017年8月8日在四川阿坝州九寨沟县发生了MS 7.0地震，这是继2008年四川汶川MS 8.0地震和四川芦山MS 7.0地震后在此地区发生的又一强震。本研究对此次地震中的66组主震记录进行了常规校正处理，基于此分析了此次地震中典型台站——九寨百合台站的地震动特征，并通过地震动的峰值加速度、反应谱参数分析了近场效应特征。研究结果表明：九寨百合台站的三分量峰值加速度都超过了100 gal，而地震动持时相对较短，并且三分量反应谱在短周期大于Ⅷ度多遇地震设计谱，小于Ⅷ度罕遇地震设计谱；由于九寨沟地震属于典型的走滑型地震，因此地震动参数的方向性特征不明显；九寨沟地震的地震动的峰值加速度以及反应谱谱值小于同等震级的芦山地震，并且小于几个典型衰减关系的预测值。对九寨沟地震的地震动参数特征研究表明，此次地震是一次震级较大、但灾害损毁程度较低的地震。Abstract: On August 8, 2017, an MS7.0 earthquake hit Aba County, Jiuzhaigou of Sichuan Province. This is the second strong earthquake occurred in this area after the Wenchuan MS8.0 earthquake in 2008 and the Lushan MS7.0 earthquake in 2013 in Sichuan. After conventional correction of the 66 sets of mainshock records, we analyzed the characteristics of the typical station, Jiuzhai Baihe, the peak ground acceleration, the response spectrum and the near-field effect of the ground motion. The results show that the peak ground acceleration of three components of Jiuzhai Baihe stations great than 100 gal, but the duration is relatively short. The response spectrum of the three components is greater than Ⅷ degree frequent seismic design spectra, less than Ⅷ degree rare earthquake design spectrum in the short period. Since the Jiuzhaigou earthquake is a typical strike-slip earthquake, the distribution of the ground motion has smaller directional characteristics. The peak ground acceleration and the response spectrum of the Jiuzhaigou earthquake is smaller than the Lushan earthquake, as well as smaller than the predicted value of several typical attenuation relationship. The characteristics of the ground motion parameters of the Jiuzhaigou earthquake show that the earthquake is the one with large magnitude and low damage degree.
-
图 6 九寨沟地震的地震动参数及芦山地震的地震动参数与典型衰减关系的比较
Figure 6. Comparison of ground motion parameters and typical attenuation relationship between the Jiuzhaigou MS7.0 earthquake and Lushan MS7.0 earthquake
表 1 不同距离范围内台站数量及其所占比例
Table 1. Number and percentage of stations in different rupture distance ranges
距离范围/km 台站数量 所占比例/% 0—50 3 4.55 50—100 4 6.06 100—200 20 30.30 > 200 39 59.09 
下载: 导出CSV
-
霍俊荣, 1989. 近场强地面运动衰减规律的研究. 哈尔滨: 中国地震局工程力学研究所. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y129938 姜治军, 2013. 中国西部基岩地震动衰减关系及场地影响系数初步研究. 哈尔滨: 中国地震局工程力学研究所. http://cdmd.cnki.com.cn/Article/CDMD-85406-1013342699.htm 四川新闻网, 2017. 地震专家: 九寨沟地震损毁程度低于同级地震的五个原因. (2017-08-11). http://scnews.newssc.org/system/20170811/000807659.html. 王珊, 张郁山, 尤贺, 2014.场地划分标准对基岩地震动参数衰减关系的影响.震灾防御技术, 9(4):759-769. doi: 10.11899/zzfy20140403 肖亮, 俞言祥, 2011.中国西部地区地震烈度衰减关系.震灾防御技术, 6(4):358-371. doi: 10.11899/zzfy20110402 新浪网, 2017. 九寨沟7. 0级地震烈度图发布: 川甘8县受影响, 大部分房屋经受住考验. (2017-08-12). http://news.sina.com.cn/o/2017-08-12/doc-ifyixipt1345658.shtml. 俞言祥, 汪素云, 2006.中国东部和西部地区水平向基岩加速度反应谱衰减关系.震灾防御技术, 1(3):206-217. doi: 10.11899/zzfy20060304 俞言祥, 李山有, 肖亮, 2013.为新区划图编制所建立的地震动衰减关系.震灾防御技术, 8(1):24-33. doi: 10.11899/zzfy20130103 张齐, 2012. 中国西部强地震动衰减关系初步研究. 哈尔滨: 中国地震局工程力学研究所. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D370615 中国地震局地球物理研究所, 2017. 2017年8月8日四川九寨沟7. 0级地震. (2017-08-11). http://www.cea-igp.ac.cn/tpxw/275883.html. 中国地震局工程力学研究所, 2017. 2017年8月8日四川九寨沟7. 0级地震强震动观测简报V2. (2017-08-13). http://www.iem.net.cn/detail.html?id=880. 中国青年网, 2017. 九寨沟地震遇难者人数上升至25人21人身份已确定. (2017-08-13). http://news.youth.cn/sh/201708/t20170813_10502594.htm. 中华人民共和国城乡建设部, 中华人民共和国国家质量监督检验检疫总局, 2010. GB 50011-2010建筑抗震设计规范. 北京: 中国建筑工业出版社. Hu J. J., Zhang W. B., Xie L. L., et al., 2015. Strong motion characteristics of the MW 6.6 Lushan earthquake, Sichuan, China-an insight into the spatial difference of a typical thrust fault earthquake. Earthquake Engineering and Engineering Vibration, 14(2):203-216. doi: 10.1007/s11803-015-0017-2 Hu J. J., Zhang Q., Jiang Z. J., et al., 2016. Characteristics of strong ground motions in the 2014 MS 6.5 Ludian earthquake, Yunnan, China. Journal of Seismology, 20(1):361-373. doi: 10.1007/s10950-015-9532-x -
点击查看大图
图(6) / 表(1)
计量
- 文章访问数: 66
- HTML全文浏览量: 50
- PDF下载量: 4
- 被引次数: 0
