Analysis on Ellipse Fitting of Hysteresis Curve in Dynamic Rriaxial Test
-
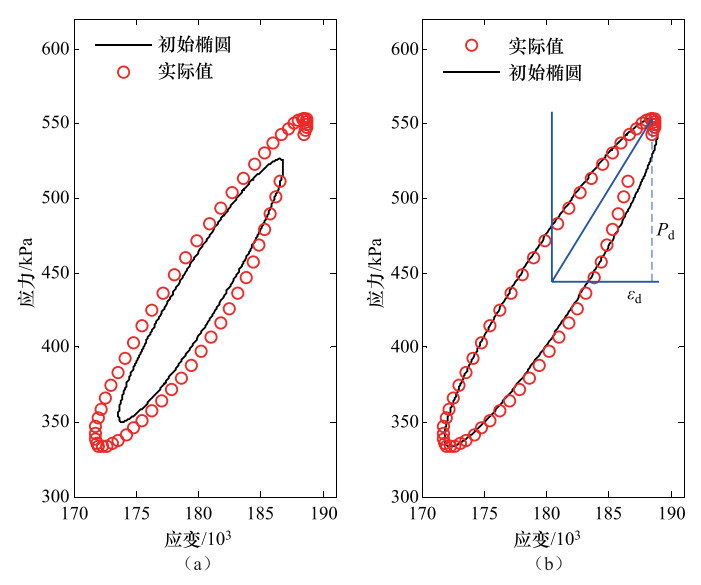
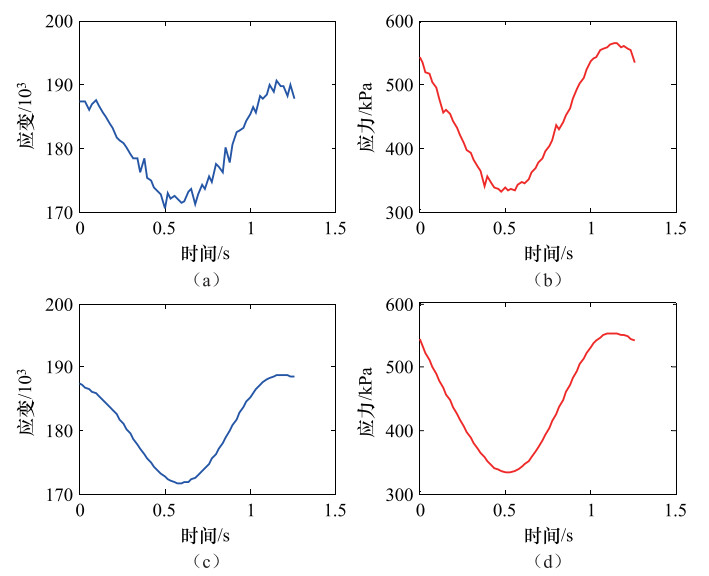
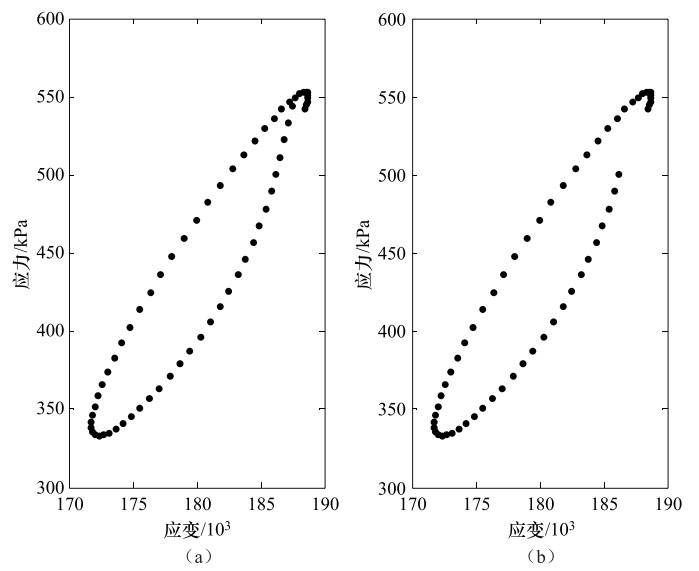
摘要: 采用正弦波形循环荷载动三轴试验获取土的动剪切模量和阻尼比的数据处理过程中通常存在两个困难：一是因为试验中存在各种噪声使滞回曲线椭圆形态不明显；二是椭圆拟合会因方法不当出现不收敛或者误差大等情况。为了在一定程度上克服第一个困难，本文将滤波技术引入到对应力应变时间序列的处理中来；为了更好地拟合滞回曲线椭圆，本文结合了主成份分析技术与椭圆的几何拟合方法，通过计算椭圆焦点位置、长半轴长度等来确定拟合椭圆，结果表明，该方法容易线性化且相对稳定，值得在动三轴数据处理中进行推广。Abstract: There exist two difficulties in the data processing of dynamic tri-axial tests when we use sinusoidal cyclic loading to obtain dynamic shear modulus and damping ratio. One difficulty is that the elliptic hysteresis curve is not clear enough due to various noises, and another one is that the procedure of fitting ellipse is divergent or the results of fitting with larger uncertainty because selected ellipse fitting method is improper. In this study, in order to overcome these difficulties to some extents, we processed time series of dynamical stress and stain with filtering technology. To fit the elliptic hysteresis curve well, we calculated the fitted ellipse by determining the two focuses and the length of the long axis of ellipse which we obtained by combining principal component analysis with ellipse geometrical fitting method. The result shows that this method is easy to linearize the nonlinear ellipse fitted problem and relatively stable, and it is worth popularizing in the dynamical tri-axial test data processing.
-
Key words:
- Dynamic tri-axial test /
- Hysteresis curve /
- Ellipse fitting /
- Geometric method /
- Filtering technology
-
图 1 确定动弹性模量和阻尼比示意图
Figure 1. Schematic diagram of calculating dynamic elastic modulus and damping ratio
图 4 椭圆拟合迭代前（a）后（b）变化示意图
Figure 4. Schematic diagrams of ellipse fitting iteration, before(a) and after(b)
图 2 应力、应变初始（（a）、（b））及滤波后（（c）、（d））的时间曲线
Figure 2. Initial time series of stress (a) and strain (b), filtered time series of stress (c) and strain (d)
图 3 手动删除异常点前（a）后（b）应力应变曲线
Figure 3. Stress-strain curves before (a) and after (b) deleted abnormity point manually
图 5 不同动剪应变下的G/Gmax及动阻尼比λd曲线
Figure 5. Curves of G/Gmax and λd at different dynamic shear strain levels
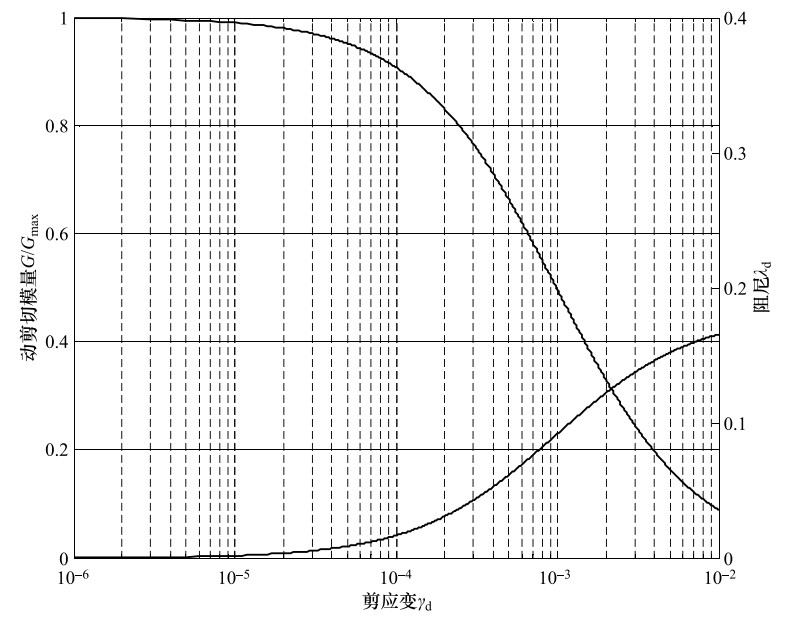
表 1 试样动三轴试验结果，不同动剪应变下的G/Gmax及λd
Table 1. The dynamical tri-axial test results of G/Gmax and λd at different shear strain levels
施加围压/kPa 土动力特性参数 动剪应变 5×10－6 1×10－5 5×10－5 1×10－4 5×10－4 1×10－3 5×10－3 1×10－2 200 G/Gmax 0.9937 0.9895 0.9505 0.9058 0.6592 0.4930 0.1633 0.0894 λd 0.0028 0.0049 0.0210 0.0372 0.0989 0.1246 0.1582 0.1641 
下载: 导出CSV
-
陈国兴, 庄海洋, 2005.基于Davidenkov骨架曲线的土体动力本构关系及其参数研究.岩土工程学报, 27(8):860-864. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=ytgc200508003&dbname=CJFD&dbcode=CJFQ 陈基伟, 2007a.椭圆直接拟合算法研究.工程勘察, (6):49-51. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=gckc200706011&dbname=CJFD&dbcode=CJFQ 陈基伟, 2007b.工程测量中一类参数曲线的拟合.大地测量与地球动力学, 27(1):100-103. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=dkxb200701021&dbname=CJFD&dbcode=CJFQ 郭可骍, 2015. 非饱和黄土的动三轴试验研究. 西安: 长安大学. 郭婷婷, 秦梅梅, 2016.土动三轴试验参数选取的理论分析与计算.工程抗震与加固改造, 38(2):144-149. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=gckz201602021&dbname=CJFD&dbcode=CJFQ 李松林, 1990.动三轴试验的原理与方法.北京:地质出版社. 南京水利科学研究院土工研究所, 2003.土工试验技术手册.北京:人民交通出版社. 彭青玉, 2003.木星土星边缘的椭圆拟合.云南天文台台刊, (4):43-48. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=ytwt200304007&dbname=CJFD&dbcode=CJFQ 申权, 李明俊, 蒋文明等, 2013.动三轴试验测试土阻尼的影响因素与不足.江西科学, 31(1):84-89. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=jskx201301023&dbname=CJFD&dbcode=CJFQ 孙静, 袁晓铭, 孙锐, 2004.土动剪切模量和阻尼比的推荐值和规范值的合理性比较.地震工程与工程振动, 24(2):125-133. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=dggc200402022&dbname=CJFD&dbcode=CJFQ 吴世明, 周健, 杨挺, 2001.土动力学理论与计算.北京:中国建筑工业出版社. 许正文, 姚连璧, 2008.基于稳健估计的直接最小二乘椭圆拟合.大地测量与地球动力学, 28(1):77-80. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=dkxb200801018&dbname=CJFD&dbcode=CJFQ 闫蓓, 王斌, 李媛, 2008.基于最小二乘法的椭圆拟合改进算法.北京航空航天大学学报, 34(3):295-298. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=bjhk200803011&dbname=CJFD&dbcode=CJFQ 杨淑莹, 张桦, 2015.模式识别与智能计算-MATLAB技术实现.3版.北京:电子工业出版社. 张茹, 何昌荣, 费文平等, 2006.固结应力比对土样动强度和动孔压发展规律的影响.岩土工程学报, 28(1):101-105. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=ytgc200601020&dbname=CJFD&dbcode=CJFQ 张涛, 2004. 中型动三轴仪的研制及城市垃圾土动力特性试验研究. 大连: 大连理工大学. 赵红芬, 何昌荣, 王莉娜, 2009.动模量阻尼的动三轴试验研究.路基工程, (4):158-160. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=ljgc200904081&dbname=CJFD&dbcode=CJFQ Hardin B. O., Black W. L., 1968. Vibration modulus of normally consolidated clay. American Society of Civil Engineers, 94(2):353-370. http://www.mendeley.com/catalog/vibration-modulus-normally-consolidated-clay/ Hardin B. O., Drnevich V. P., 1972. Shear modulus and damping in soils. Journal of the Soil Mechanics and Foundations Division, 98(7):667-692. Martin P. P., Seed H. B., 1982. One-dimensional dynamic ground response analyses. Journal of the Geotechnical Engineering Division, 108(7):935-952. http://cedb.asce.org/cgi/WWWdisplay.cgi?34463 Seed H. B., Idriss I. M., 1970. Soil moduli and damping factors for dynamic response analyses. Report No EERC70-10. Berkeley:Earthquake Engineering Research Center, University of California Berkeley. -
点击查看大图
计量
- 文章访问数: 115
- HTML全文浏览量: 55
- PDF下载量: 5
- 被引次数: 0
