TMD Control and Analysis of Cranes under Earthquake
-
摘要: 虽然建筑施工周期内地震致险概率并不高,但是由于塔吊使用极其广泛,塔吊致险概率并不低于建筑结构,故而针对塔吊的减震措施亟需研究。本文以某实际超高层建筑施工使用的动臂式塔吊为研究对象,根据塔吊自身和附着于超高层建筑后的动力特性,研究了TMD装置的不同方案对塔吊地震响应的控制效果。结果表明:① TMD装置对于属于高耸结构的塔吊减震控制非常有效;② 设置在塔身顶部的双向TMD不仅可以有效减小塔身偏摆,也可以间接有效地控制起重臂的竖向振动;③ 由于超高层建筑-塔吊结构高阶振型影响明显,此TMD装置对塔吊塔身控制效果不稳定,但对于起重臂仍能起到良好的控制作用,故而此TMD装置可以使用在附着在超高层建筑上的施工塔吊,对于塔身的振动控制仍需进一步研究。Abstract: Due to the universality and the characteristics of cranes, cranes risk probability is not lower than building structure, so It's nessesary to research the crane shock absorption measures although during the construction period, the earthquake risk probability is not high. Based on its dynamic characteristics of cranes and attached to the high-rise building, the dynamic characteristics of the TMD of different schemes on the earthquake response of the tower crane control effect. The results show that:① TMD for tall structures of cranes seismic vibration control is effective. ② In order to control cranes tower deflection of lateral and vertical vibration boom, set up in the tower at the top of the two-way TMD can't only effectively reduce the deflection of the tower, but also can indirectly effectively control the crane boom vertical vibration. ③ The TMD device has a good control effect on the tower crane body, but it also has a good control effect for the boom, so the TMD device can be used in the super high-rise building on the construction tower crane, but for the tower body's vibration control still need further study.
-
Key words:
- Cranes /
- TMD /
- Super high-rise building /
- Analysis on seismic response
-
表 1 结构周期和振型质量参与系数
Table 1. Natural period and participation mass ratio of structures
模态/阶 周期/s UX UY SX SY 1 6.24 5.40E-07 0.3829 5.4E-07 0.3829 2 4.72 0.3353 8.31E-05 0.3353 0.3830 3 2.61 0.0003 0.3923 0.3356 0.7753 4 2.14 0.5070 4.32E-05 0.8426 0.7753 5 0.92 7.57E-05 4.46E-05 0.8427 0.7754 注:UX、UY分别为某一振型在X、Y方向的质量参与比;SX、SY为X、Y方向的质量参与比振型顺序累积值。 表 2 Sadek法TMD参数表
Table 2. TMD parameters of the table by Sadek
参数 数值 单位 结构总质量 198.83 t 一阶振型质量参与系数 0.383 m1* 76.15 t μ 0.05 mTMD 3.8 t TMD个数 1 单个TMD质量 3.8 t ε1* 0.03 δ 0.9461 εTMD 0.2468 结构振型频率f* 0.1656 Hz 结构振型圆频率ω* 1.0397 rad/s ωTMD 0.9837 rad/s KTMD 3677.1296 N/m CTMD 1845.106 N·s/m 表 3 结构周期对比(单位:s)
Table 3. Periods of model
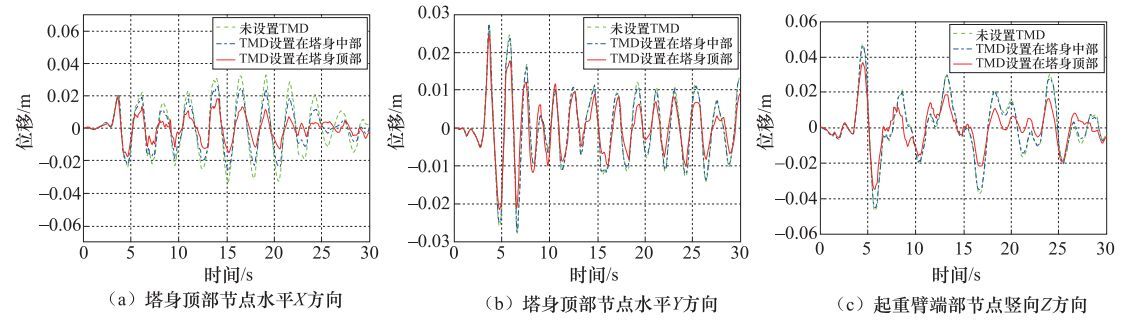
方案 第一阶 第二阶 第三阶 未设置TMD 6.24391 4.72713 2.61045 TMD设置在塔身中部 6.24397 4.72714 2.60781 TMD设置在塔身顶部 6.24402 4.73268 2.59619 表 4 控制位移最大值及减震率汇总
Table 4. Maximum displacement and shock absorption rate
输入地震波 方向 减震前最大位移/m 方案1 方案2 最大位移/m 减震率/% 最大位移/m 减震率/% Taft波 X 0.031 0.024 22.58 0.020 35.48 Y 0.029 0.028 3.45 0.026 10.34 Z 0.048 0.047 2.08 0.036 25.00 RSN164-147波 X 0.027 0.024 11.11 0.011 59.26 Y 0.023 0.022 4.34 0.015 34.78 Z 0.060 0.052 13.33 0.041 31.67 El-Centro波 X 0.052 0.046 11.54 0.013 75.00 Y 0.077 0.069 10.39 0.048 3.66 Z 0.153 0.150 1.96 0.092 39.87 注:表中X、Y、Z分别对应与塔身顶部X方向、塔身顶部Y方向和起重臂端部Z方向位移。方案1指塔身中部安装TMD装置;方案2指塔身顶部安装TMD装置。 表 5 控制位移最大值及减震率汇总
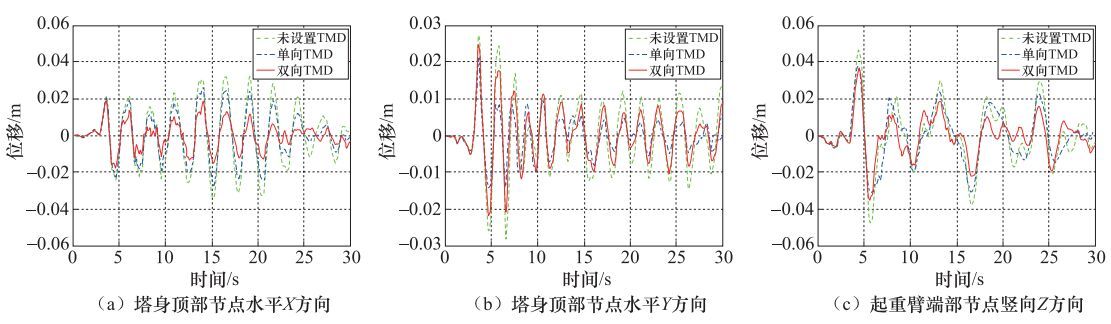
Table 5. Maximum displacement and shock absorption rate
输入地震波 方向 减震前最大位移/m 方案1 方案2 最大位移/m 减震率/% 最大位移/m 减震率/% Taft波 X 0.031 0.020 35.48 0.027 12.90 Y 0.029 0.026 10.34 0.021 27.59 Z 0.048 0.036 25.00 0.039 18.75 RSN164-147波 X 0.027 0.011 59.26 0.024 11.11 Y 0.023 0.015 34.78 0.012 47.83 Z 0.060 0.041 31.67 0.058 3.33 El-Centro波 X 0.052 0.013 75.00 0.043 17.31 Y 0.077 0.048 37.66 0.026 66.23 Z 0.153 0.092 39.87 0.133 13.07 注:表中X、Y、Z分别对应与塔身顶部X方向、塔身顶部Y方向和起重臂端部Z方向位移。方案1指塔身顶部安装双向TMD装置;方案2指塔身顶部安装单向TMD装置。 表 6 70层建筑-塔吊模型周期对比(单位:s)
Table 6. Periods of model by 70 layer building-crane
方案 第一阶 第二阶 第三阶 未设置TMD 6.1721 6.0437 5.3924 设置TMD 6.1743 6.0451 5.3931 表 7 TMD参数表
Table 7. TMD parameters of the table by Sadek
参数 方案1 方案2 单个TMD质量/t 3.8 3.8 结构振型阻尼比取值ε1* 0.05 0.05 TMD与振型频率最佳频比δ 0.9420 0.9420 TMD阻尼比εTMD 0.2658 0.2658 结构振型频率f*/Hz 0.1633 0.1854 结构振型圆频率ω*/rad·s-1 1.0226 1.1643 TMD最佳圆频率ωTMD/rad·s-1 0.9633 1.0965 TMD刚度KTMD/N·m-1 3526.20 4568.79 TMD阻尼系数CTMD/N·s·m-1 1945.94 2215.02 表 8 控制位移最大值及减震率汇总
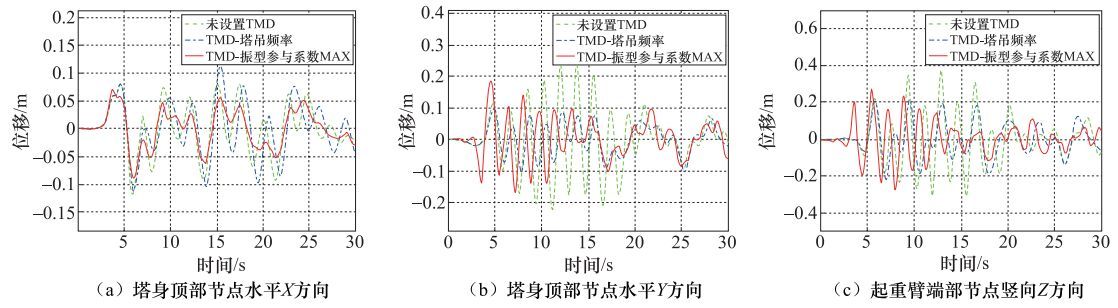
Table 8. Maximum displacement and shock absorption rate
输入地震波 方向 减震前最大位移/m 方案1 方案2 最大位移/m 减震率/% 最大位移/m 减震率/% Taft波 X 0.075 0.119 -58.67 0.069 8.00 Y 0.237 0.097 59.07 0.192 18.99 Z 0.389 0.205 47.31 0.278 28.53 RSN164-147波 X 0.153 0.153 0 0.149 2.61 Y 0.178 0.165 7.30 0.164 7.87 Z 0.227 0.227 0 0.163 28.19 El-Centro波 X 0.151 0.158 -4.64 0.103 31.79 Y 0.513 0.382 25.54 0.523 -1.95 Z 0.579 0.579 0 0.491 15.20 注:表中X、Y、Z分别对应与塔身顶部X方向、塔身顶部Y方向和起重臂端部Z方向位移。方案1指计算时对应超高层建筑-塔吊模型第一阶自振周期;方案2指计算时对应超高层建筑-塔吊模型第三阶自振周期。 -
何银晖, 谷立臣, 姬鹏斌, 2012.基于ANSYS的塔式起重机抗震分析.机械设计与制造, (7):188-190. http://www.cnki.com.cn/Article/CJFDTOTAL-JSYZ201207069.htm 何志军, 丁洁民, 陆天天, 2014.上海中心大厦巨型框架-核心筒结构竖向地震作用反应分析.建筑结构学报, 35(1):27-33. http://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201401004.htm 吉军, 张辉, 张顺利等, 2009.塔式起重机地震响应研究.西北师范大学学报(自然科学版), 45 (4):43-47. http://cdmd.cnki.com.cn/Article/CDMD-10141-1012395206.htm 李云岭, 艾兵, 李博, 2011.塔式起重机在地震作用下的受损原因及动态分析现状.特种结构, 28 (2):66-68. http://www.cnki.com.cn/Article/CJFDTOTAL-TZJG201102031.htm 刘小萌, 张长会, 卢志强等, 2015.黏滞阻尼器在煤矿井塔结构抗震加固中的应用.震灾防御技术, 10(1):126-134. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?flag=1&file_no=20150113&journal_id=zzfyjs 卿龙邦, 姚雄, 肖成志等, 2013.外爬式塔吊对高层钢板剪力墙结构影响的分析.华北地震科学, 31(S):24-27. http://www.cnki.com.cn/Article/CJFDTOTAL-HDKD2013S1007.htm 王武奇, 2009. QTZ630型塔式起重机结构有限元分析及地震影响研究. 西安: 长安大学. 谢瑞, 田太明, 田奇, 2009.汶川地震中西安市塔式起重机的损毁分析.起重运输机械, (4):1-3. http://www.cnki.com.cn/Article/CJFDTOTAL-QZJJ200904001.htm 阎红霞, 杨庆山, 张丽英, 2010. ABAQUS在超高层结构动力弹塑性分析中的应用.震灾防御技术, 5(1):108-115. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?flag=1&file_no=20100113&journal_id=zzfyjs 闫维明, 纪金豹, 蒋华戈等, 2010.新型悬吊式TMD及其在某标志塔风振控制中的应用.建筑结构学报, 31(2):55-60. http://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201002007.htm 姚佳琳, 张家伟, 王泽云, 2014.超高层"框-筒"结构中内爬式塔吊附着节点力学性能分析.四川建筑科学研究, 40(2):345-349, 360. http://www.cnki.com.cn/Article/CJFDTOTAL-ACZJ201402086.htm 殷伟希, 谭平, 周福霖等, 2010.近场地震动下偏心结构的减震控制研究.震灾防御技术, 5(2):199-207. http://zzfy.eq-j.cn/zzfyjs/ch/reader/view_abstract.aspx?flag=1&file_no=20100206&journal_id=zzfyjs 章崇任, 2007.日本内爬式塔式起重机的发展趋势.工程机械, 38(4):73-75. http://www.cnki.com.cn/Article/CJFDTOTAL-GCJA200704022.htm 张俊卫, 2014. 超高层建筑的风致横风向响应分析和TMD控制. 大连: 大连理工大学. http://cdmd.cnki.com.cn/Article/CDMD-10141-1015572495.htm Kim J., Lee S., Choi H., 2013. Progressive collapse resisting capacity of moment frames with viscous dampers. The Structural Design of Tall and Special Buildings, 22(5):399-414. doi: 10.1002/tal.v22.5 Longarini N., Zucca M., 2014. A chimney's seismic assessment by a tuned mass damper. Engineering Structures, 79:290-296. doi: 10.1016/j.engstruct.2014.05.020 Mijailović R., Kastratović G., 2009. Cross-section optimization of tower crane lattice boom. Meccanica, 44(5):599-611. doi: 10.1007/s11012-009-9204-4 Otani A., Nagashima K., Suzuki J., 2002. Vertical seismic response of overhead crane. Nuclear Engineering and Design, 212(1-3):211-220. doi: 10.1016/S0029-5493(01)00483-6 Sadek F., Mohraz B., Taylor A. W., et al., 1997. A method of estimating the parameters of tuned mass dampers for seismic applications. Earthquake Engineering & Structural Dynamics, 26(6):617-635. doi: 10.1002/%28SICI%291096-9845%28199706%2926%3A6%3C617%3A%3AAID-EQE664%3E3.0.CO%3B2-Z Wang P., Scherler D., Liu-Zeng J., et al., 2014. Tectonic control of Yarlung Tsangpo Gorge revealed by a buried canyon in Southern Tibet. Science, 346(6212):978-981. doi: 10.1126/science.1259041 -




 下载:
下载: