Effect of Random Numbers of Bedrock Input Time Histories on the PGA from Site Response Analyses
-
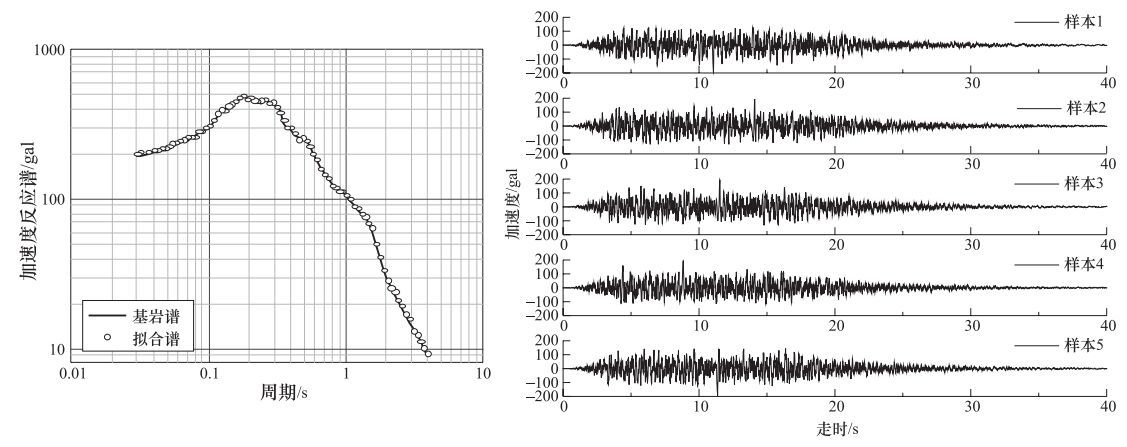
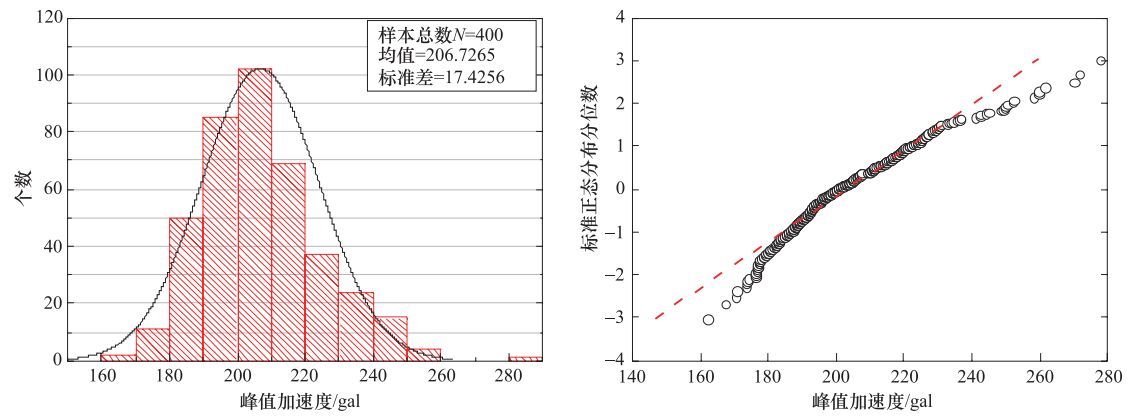
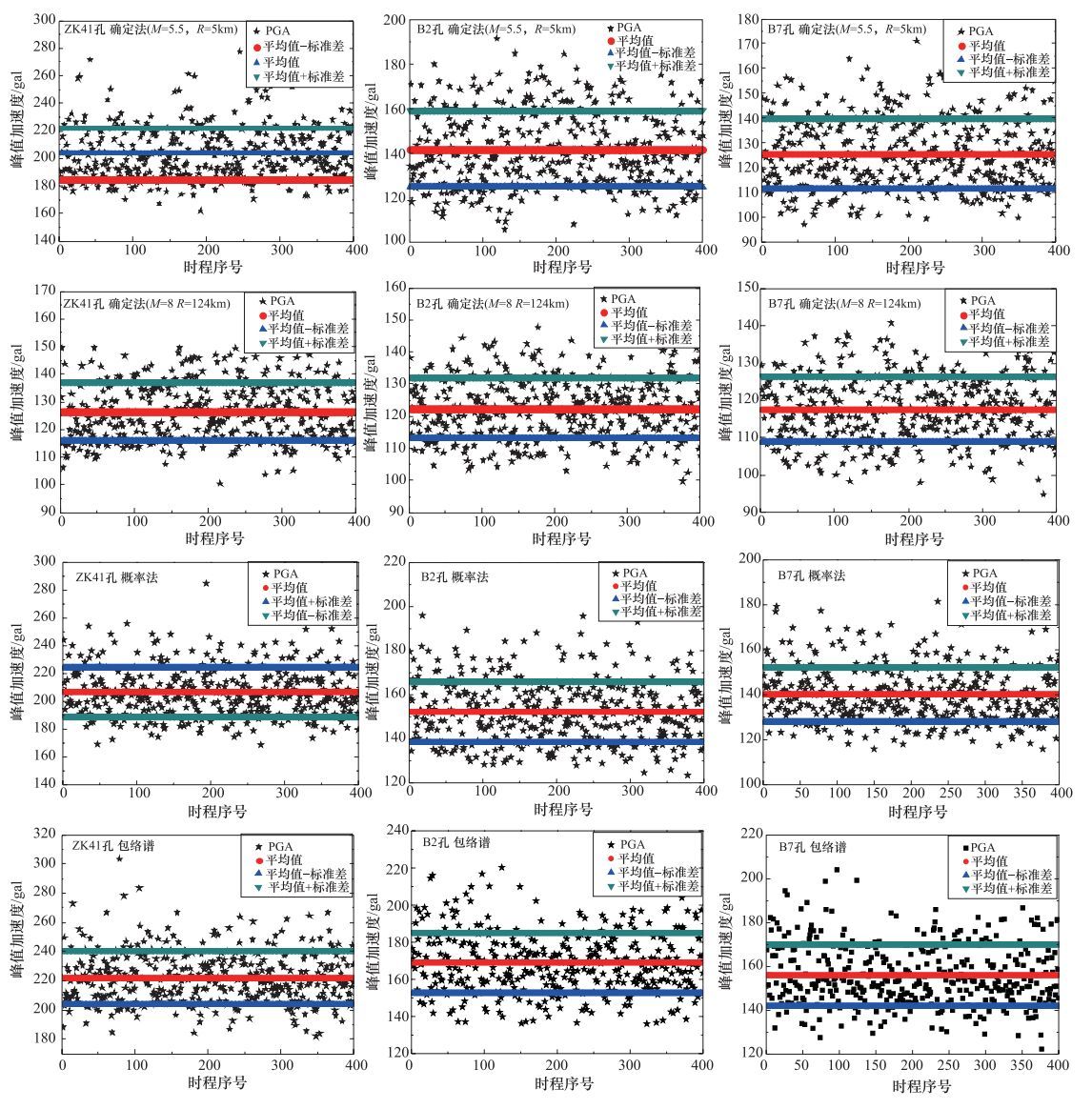
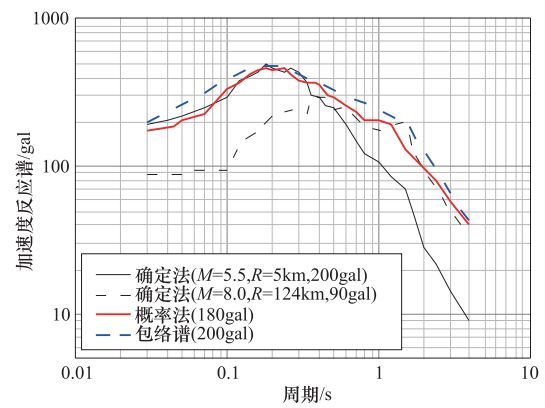
摘要: 研究基岩输入时程随机数对场地峰值加速度的影响，对核电厂设计地震动参数的合理确定具有重要意义。本文选取了某重要核电站场地具有代表性的3个钻孔，建立了场地计算模型。根据确定性方法、概率性方法得到的基岩反应谱及其包络谱，基于不同随机数，分别合成了400条基岩输入时程。采用LSSRLI-1程序进行了场地地震反应，根据4800个计算结果，研究了不同随机数对地表峰值加速度的影响，给出了自然对数下峰值加速度标准差的估计，揭示了峰值加速度的分布规律，提出了对核电厂设计地震动参数合理确定的建议。Abstract: It is important to study the influence of the random numbers of bedrock input time histories on the peak ground acceleration (PGA) from site response, analyses and is of great significance for the determination of design ground motion parameters for nuclear power plants. Three representative boreholes of an nuclear power plant site were selected, and the site calculation models were established. Respectively, according to deterministic methods and probabilistic methods, the bedrock response spectra and the envelope spectra were determined. Based on different random numbers, 400 bedrock input time histories were respectively synthesized. Based on the LSSRLI-1 program, the seismic responses of the sites were studied. According to the results of 4800 calculations, we analyzed the effects of different random numbers on the surface PGA. The estimation of the standard deviation of peak acceleration under natural logarithm was given, and the distribution of PGA was revealed. Suggestions on reasonable determination of design ground motion parameters of nuclear power plant are put forward.
-
Key words:
- Random number /
- Artificial ground motion /
- Peak ground acceleration /
- Nuclear power plant
-
引言
悬索桥结构主要由锚碇、索塔、缆索系统、加劲梁和附属结构组成，具有结构简单、轻便、易于标准化、构件易运输、方便悬吊拼装、施工限制较少等特点（铁道部大桥工程局桥梁科学研究所，1996；钱炜，2007），是特大桥梁的主要类型（李光军，2012）。地震是造成桥梁结构破坏的主要原因之一，桥梁是联系外界与地震灾区的重要纽带，桥梁一旦破坏，将中断通往灾区的通道，影响救灾工作进展，造成较大损失（刘润舟，2008）。因此，对悬索桥结构进行地震响应分析具有重要意义。国内外学者已开展了大跨度桥梁多点激励地震响应研究，如许基厚等（2019）对非对称单侧混合梁斜拉桥多点激励地震响应进行研究，分析了行波效应对塔顶、主梁、塔底等关键位置动力响应的影响，并研究了不同入射角对桥梁动力响应的影响，认为多点激励下主塔内力计算结果偏小，而主梁内力计算结果偏大，地震激励对非对称大跨度斜拉桥内力产生较大影响，内力变化可达20%；张凡等（2016）对不同波速下斜拉桥地震响应进行了分析，认为波速的影响显著；王再荣等（2016）分析行波效应下斜拉桥地震响应，得出辅助墩耗能降低、桥塔损伤增大的结论；刘旭政等（2018）考虑2种地震波和3种视波速的不同组合，以一座实际工程高桩大跨度连续刚构桥为例，研究行波效应对桥梁地震响应的影响，认为随着视波速的增大，行波效应对桥梁内力的影响程度减小；梅泽洪等（2017）研究了考虑局部场地效应桥梁结构在非一致激励下地震响应的特点，认为下部结构响应所受影响较小，而上部结构所受影响明显，考虑行波效应的非一致激励对桥梁地震响应有减弱效果；黎璟等（2019）以铁路工程实际桥梁为例，研究了非一致激励下大跨度铁路斜拉桥地震响应规律，认为在非一致激励下塔顶位移响应峰值与墩底弯矩响应峰值均随着相位差呈周期性变化，且变化周期与结构一阶自振周期基本一致。
本文选取某三跨两铰连续体系悬索桥，已有研究结果表明线性分析方法和非线性分析方法得到的该桥地震响应结果相近（Fleming等，1980；李丽等，2018a）。因此利用大型通用有限元软件ANSYS建立三维弹性有限元模型，分析一致激励与多点激励下悬索桥地震响应，研究其抗震性能。
1. 桥梁结构动力响应分析方法
桥梁结构动力响应分析方法主要包括一致激励动态时程分析方法及多点激励动态时程分析方法，目前多点激励动态时程分析方法的应用较多，该方法考虑地震行波效应和局部场地效应，对各独立基础或支撑结构输入不同的设计反应谱或加速度时程进行计算（张沧海，2011），主要包括相对运动法和大质量法（范立础等，2001；Leger等，1990）。相对运动法通过支撑点的加速度时程计算非支撑点的动力响应。大质量法是对结构模型进行动力等效的分析方法，在处理多点激励问题时需解除支撑点沿地震作用方向的约束，并赋予节点大质量，其值通常远大于结构体系的总质量（苏成等，2008）。本文采用相对运动法计算悬索桥在多点激励下的响应。
2. 桥梁结构概况
三跨连续悬索桥主跨124m，主梁设计为连续加劲梁，加劲梁采用正交异性板流线形扁平钢箱梁，梁高1.88m，宽（含风嘴）10.8m；纵向分配梁宽0.16m，厚0.28m；纵向斜腹杆，横向内侧竖杆，横向内、外侧斜腹杆截面宽度均为0.16m，厚度均为0.2m；纵向上、下弦杆截面宽度均为0.3m，厚度均为0.2m；纵向竖杆截面宽0.2m，厚0.18m；横向外侧竖杆截面宽0.2m，厚0.24m；横向上弦杆截面宽0.18m，厚0.24m；横向下弦杆截面宽0.18m，厚0.2m；抗风桁架截面宽0.12m，厚0.12m。主塔为H形，塔高36m，南、北桥塔未设置上、下横梁。塔柱截面宽2m，厚4m；柱间连接件截面宽4m，厚2m。桥面以上有3根主缆，南、北边跨吊索各12根，主跨共30根，索间距4m。主缆截面直径为0.079m，吊索截面直径为0.039m。桥梁结构各构件材料物理参数见表 1。
表 1 桥梁结构材料物理参数Table 1. The material physical parameters of bridge structure构件 材料 弹性模量/Pa 泊松比 密度/kg·m-3 主缆 钢丝绳 21.0×1010 0.167 7850 吊索 钢丝绳 21.0×1010 0.167 7850 加劲桁架、纵梁 C30混凝土 3.0×1010 0.300 2500 桥塔、桥面板 C20混凝土 2.8×1010 0.300 2500 3. 输入地震动
选取常用的Kobe地震波对悬索桥进行地震响应分析，顺桥向输入的加速度时程曲线如图 1，加速度峰值为0.345g，持时为24.79s。
图 1 输入Kobe波加速度时程曲线（顺桥向）Figure 1. The input Kobe wave of acceleration time history curve (Along the bridge)对于大跨度悬索桥，输入地震动时常将水平地震系数的1/2或2/3作为竖向地震系数，组合方式通常为顺桥向与竖向组合、横桥向与竖向组合（李国豪，2003），因此，进行一致激励下的地震响应分析时，本文将竖向地震系数取为水平地震系数的1/2，并选取顺桥向与竖向组合；进行多点激励下的地震响应分析时，将竖向地震系数取为水平地震系数的1/2，先对加速度时程曲线进行2次积分，第1次积分得到速度时程曲线，并将其进行基线校正，将校正后的速度时程曲线再次积分并进行基线校正，得到位移时程曲线，如图 2。
图 2 Kobe波位移时程曲线（顺桥向）Figure 2. The input Kobe wave of displacement time history curve (Along the bridge)多点激励位移输入位置为图 3中①-④桥梁支座位置，计算时考虑不同支座输入波形相位滞后现象，采用对不同支座延迟输入位移时程的方法考虑行波效应（刘春城等，2004；王蕾等，2006；严琨等，2017），根据大跨建筑结构多点输入地震响应计算结果（李丽等，2018b；景鹏旭等，2017）与抗震设计方法研究结果（江洋，2010），取视波速为1000m/s，根据支座间距计算各支座位移输入延迟时间，见表 2。
图 3 桥梁结构立面图及荷载激励点布置Figure 3. The elevation and load excitation point layout of the bridge表 2 输入位移时程延迟时间（s）Table 2. The delay time of input displacement time history (s)支座编号 ① ② ③ ④ 时间间隔 0.000 0.050 0.174 0.224 4. 有限元模型的建立
应用大型通用有限元软件ANSYS建立悬索桥三维有限元模型（图 4），应用link10单元模拟主缆及吊索，应用beam4单元模拟加劲桁架、纵向分配梁、抗风桁架、桥塔，应用shell63单元模拟桥面板。主缆及吊索初应变设为0.0043，先对结构进行重力分析，得到结构初始应力，然后对其进行模态分析，计算桥梁结构前2阶振型圆频率，应用APDL语言编制求解瑞利阻尼系数α和β：
ALPHAD, 2*DAMPRATIO*FREQ1*2*3.1415926
BETAD, 2*DAMPRATIO/(FREQ1*2*3.1415926)
5. 地震响应分析结果
计算得到主梁位移及南、北桥塔塔柱沿柱高方向的位移、轴力、剪力及弯矩包络图，如图 5-7。
图 5 主梁顺桥向最大位移包络图Figure 5. Envelope diagram of maximum displacement of main beam along bridge direction
图 6 南桥塔纵向位移、轴力、剪力及弯矩包络图Figure 6. The envelope of displacement, axial force, shearing force and bending moment of the occurrence bridge tower longitudinal
图 7 北桥塔纵向位移、轴力、剪力及弯矩包络图Figure 7. The envelope of displacement, axial force, shearing force and bending moment of the north bridge tower longitudinal由图 5可知，多点激励下主梁最大位移略高于一致激励下主梁最大位移，总体变化不大。由图 6、图 7可知，一致激励下南、北桥塔沿塔高的位移、轴力、剪力及弯矩计算结果相同，这符合有限元计算基本原理。多点激励下南、北桥塔计算结果不对称，说明地震波输入方式对计算结果具有一定影响，由于本研究中悬索桥跨度不大，所以一致激励和多点激励下计算结果差别不大。
6. 结语
本文对某对称悬索桥在一致激励及视波速1000m/s的多点激励下的地震响应进行分析，并对计算结果进行分析。计算结果表明地震波输入方式对模拟结果具有一定影响，计算结果存在一定差异，主梁在多点激励下的位移计算结果略高于一致激励下的计算结果，桥塔最大位移发生在塔中与塔顶之间，最大弯矩、轴力、剪力均发生在塔根处。
-
图 2 基岩反应谱拟合情况和样本时程（确定法：M=5.5，R=5km）
Figure 2. The fitting of bedrock response spectrum and the sample time histories (deterministic method: M=5.5, R=5km)
图 3 基岩地震动反应谱对目标谱拟合情况和样本时程（概率法）
Figure 3. The fitting of bedrock response spectrum and the sample time histories (probabilistic method)
图 5 不同钻孔不同输入下的地表PGA分布图
Figure 5. Distribution of the surface PGA for different boreholes with different inputs
表 1 ZK41钻孔计算参数
Table 1. Calculation parameters of ZK41 borehole
土层序号 土性描述 层厚/m 动三轴序号 剪切波速/m·s-1 密度/kg·m-3 1 粉质粘土 3.9 1 105 1810 2 粉砂 3.1 2 156 1940 3 粉砂 3.0 2 254 1940 4 粉砂 3.4 2 289 1940 5 粉质粘土 3.6 3 264 1920 6 粉质粘土 4.0 3 224 1920 7 粉质粘土 4.2 3 218 1920 8 粉质粘土 6.8 3 248 1920 9 粉质粘土 5.0 3 320 1920 10 粉质粘土 5.7 3 344 1920 11 粉砂 1.6 2 357 1940 12 玄武岩 29.9 7 1410 2430 13 玄武岩 16.0 7 2169 2500 14 玄武岩 2.7 7 1500 2430 15 火山角砾岩 18.1 7 1463 2100 16 火山角砾岩 18.0 7 1552 2150 17 火山角砾岩 24.0 7 1588 2200 18 火山角砾岩 18.0 7 1552 2150 19 火山角砾岩 12.0 7 1605 2200 20 火山角砾岩 15.0 7 1552 2150 21 粉质黏土 18.0 4 582 2060 22 粉质黏土 18.0 4 608 2060 23 粉质黏土 18.0 4 635 2060 24 粉质黏土 15.0 5 667 2070 25 粉质黏土 12.0 5 688 2070 26 粉质黏土 18.0 5 706 2070 27 粉质黏土 12.8 5 715 2070 28 粉细砂 1.3 6 715 2060 29 粉质黏土 9.9 5 724 2080 30 粉质黏土 16.5 5 730 2100 31 计算基底 7 730 2200 
下载: 导出CSV
表 2 土层样品动力非线性曲线参数
Table 2. Parameters of dynamic nonlinear curve of the soil
序号 模量比与阻尼比 剪应变γ/10-4 0.05 0.1 0.5 1 5 10 50 100 1 G/Gmax 0.993 0.987 0.937 0.881 0.718 0.560 0.203 0.113 λ 0.004 0.007 0.028 0.045 0.060 0.098 0.204 0.236 2 G/Gmax 0.992 0.984 0.925 0.861 0.664 0.497 0.165 0.090 λ 0.004 0.007 0.025 0.036 0.074 0.120 0.239 0.273 3 G/Gmax 0.994 0.989 0.946 0.897 0.728 0.572 0.211 0.118 λ 0.005 0.009 0.030 0.041 0.062 0.086 0.189 0.228 4 G/Gmax 0.993 0.986 0.943 0.905 0.834 0.763 0.439 0.281 λ 0.005 0.010 0.034 0.048 0.068 0.081 0.157 0.179 5 G/Gmax 0.995 0.991 0.955 0.915 0.746 0.595 0.227 0.128 λ 0.002 0.004 0.018 0.031 0.056 0.094 0.203 0.238 6 G/Gmax 0.992 0.985 0.934 0.897 0.831 0.757 0.453 0.293 λ 0.001 0.003 0.012 0.018 0.035 0.050 0.104 0.120 7 G/Gmax 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 λ 0.050 0.050 0.050 0.050 0.050 0.050 0.050 0.050
下载: 导出CSV
表 3 不同钻孔峰值加速度的统计值
Table 3. The statistical values of PGA from different boreholes
钻孔 基岩谱 PGA平均值 PGA标准差 PGA最大值 85%分位数 90%分位数 95%分位数 ZK41 M5.5 204 18.9 278 222 227 237 M8.0 127 10.7 158 139 142 146 概率法 207 17.4 285 225 231 239 包络谱 222 18.3 303 240 246 254 B2 M5.5 142 17.1 192 163 166 172 M8.0 123 9.5 148 133 136 139 概率法 152 14.0 196 166 172 178 包络谱 169 16.5 220 186 192 197 B7 M5.5 126 14.3 171 142 147 151 M8.0 118 8.7 141 128 130 133 概率法 140 12.4 182 153 158 163 包络谱 154 14.3 204 172 177 182
下载: 导出CSV
表 4 不同钻孔峰值加速度对数的统计值
Table 4. The statistical values of logarithmic PGA from different boreholes
钻孔 基岩谱 对数平均值 σln σlnAmax σlnA85 σlnA90 σlnA95 ZK41 M5.5 5.312 0.090 0.315 0.091 0.114 0.155 M8.0 4.838 0.084 0.225 0.096 0.116 0.145 概率法 5.329 0.083 0.322 0.088 0.116 0.146 包络谱 5.401 0.081 0.314 0.081 0.104 0.135 B2 M5.5 4.948 0.119 0.309 0.145 0.167 0.200 M8.0 4.807 0.077 0.191 0.083 0.106 0.129 概率法 5.021 0.091 0.258 0.092 0.124 0.159 包络谱 5.125 0.097 0.270 0.101 0.131 0.159 B7 M5.5 4.827 0.113 0.316 0.128 0.161 0.192 M8.0 4.767 0.074 0.182 0.082 0.097 0.123 概率法 4.939 0.086 0.262 0.092 0.122 0.157 包络谱 5.046 0.090 0.272 0.100 0.128 0.156 平均值 5.034 0.091 0.269 0.098 0.123 0.154
下载: 导出CSV
表 5 峰值加速度的估计值
Table 5. List of estimated PGA
钻孔 基岩谱 序号 PGA最大值 85%分位数 90%分位数 95%分位数 ZK41 M5.5 1 267 225 230 237 M8.0 2 166 140 143 148 概率法 3 271 229 233 240 包络谱 4 291 245 250 258 B2 M5.5 5 186 157 160 165 M8.0 6 161 136 139 143 概率法 7 199 168 171 177 包络谱 8 221 187 191 196 B7 M5.5 9 165 139 142 146 M8.0 10 155 130 133 137 概率法 11 183 155 158 163 包络谱 12 202 170 174 179
下载: 导出CSV
表 6 输入时程数量对峰值加速度的影响及估计
Table 6. Influence and estimation of the number of input time histroies on PGA
时程序号 地表PGA/gal PGAm PGAs PGAmax 1—5 222 188 249 203 208 214 249 280 6—10 212 229 210 227 199 215 238 282 11—15 208 220 243 210 273 231 273 302 16—20 212 214 223 212 229 218 241 286 21—30 208 206 219 255 233 227 255 297 220 223 231 251 220 31—40 224 242 191 202 219 221 249 289 202 222 227 249 230 41—50 234 217 237 203 209 218 243 286 225 205 200 243 210 51—70 199 227 224 208 215 219 267 287 208 209 234 209 227 267 231 229 225 226 210 217 196 185 235 71—90 220 212 228 241 236 229 303 303 200 207 226 303 221 201 207 239 243 278 224 215 247 236 201
下载: 导出CSV
-
曹均锋, 冯伟栋, 孟凡月等, 2013.剪切波速对场地地表地震动参数的影响.震灾防御技术, 8 (3):252-260. doi: 10.11899/zzfy20130304 国家地震局, 1998. GB 50267-97核电厂抗震设计规范. 北京: 中国计划出版社. 李建亮, 李福海, 彭晋川等, 2015.不同的地震动输入面对地震反应分析结果的影响.震灾防御技术, 10(3):522-530. doi: 10.11899/zzfy20150305 李小军, 2006.工程场地地震安全性评价工作及相关技术问题.震灾防御技术, 1(1):15-24. doi: 10.11899/zzfy20060103 卢寿德, 2006. GB 17741-2005《工程场地地震安全性评价》宣贯教材.北京:中国标准出版社. 吕悦军, 彭艳菊, 兰景岩等, 2008.场地条件对地震动参数影响的关键问题.震灾防御技术, 3 (2):126-135. doi: 10.11899/zzfy20080203 沈得秀, 王庆民, 许洪泰等, 2014.土层剪切波速测试中的不确定性对场地地震动参数的影响分析——以Ⅲ类场地为例.震灾防御技术, 9(2):244-251. doi: 10.11899/zzfy20140209 孙锐, 袁晓铭, 刘晓键, 2009.动剪切模量比与剪切波速对地震动影响及等量关系研究.岩土工程学报, 31(8):1267-1274. http://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200908021.htm 王冲, 薄景山, 齐文浩等, 2011.输入界面对地表加速度峰值的影响.地震工程与工程振动, 31(6):55-61. http://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201106008.htm 张海, 李帆, 阳芳, 2011.土层参数随机性对多层土模型传递函数的影响.山东农业大学学报(自然科学版), 42(4):555-560. http://www.cnki.com.cn/Article/CJFDTOTAL-SCHO201104018.htm 赵松戈, 胡聿贤, 廖旭, 2000.土层参数的随机性对场地传递函数的影响.地震工程与工程振动, 20(2):7-12. http://cdmd.cnki.com.cn/Article/CDMD-10056-2004075399.htm 中国地震局地质研究所, 中国地震灾害防御中心, 广西工程防震研究院, 2013a. 国核广西合浦核电项目初步可行性研究阶段地震地质专题报告. 北京. 中国地震局地质研究所, 中国地震灾害防御中心, 江苏省地质勘察技术院, 2013b. 中电投广东湛江核电项目初步可行性研究阶段地震地质专题报告. 北京. 中国地震局地质研究所, 中国地震灾害防御中心, 2014. 河北海兴核电厂可行性研究阶段工程场地地震安全性评价. 北京. 中国地震局地质研究所, 中国地震灾害防御中心, 2016. 中电投广东湛江项目可行性研究阶段工程场地地震安全性评价. 北京. 周春海, 2014.基岩人造地震动随机数对地表地震动参数的影响.世界地震工程, 30(4):89-93. http://www.cnki.com.cn/Article/CJFDTOTAL-SJDC201404013.htm EPRI, 2012. Seismic evaluation guidance:screening, prioritization and implementation details (SPID) for the resolution of fukushima near-term task force recommendation 2.1:seismic. Palo Alto, California, U.S.A.:EPRI. Newmark N. M., Blume J. A., Kapur K. K., 1973. Seismic design spectra for nuclear power plants. Journal of the Power Division, 99(2):287-303. http://cedb.asce.org/CEDBsearch/record.jsp?dockey=0020760 Rathje E. M., Kottke A. R., Trent W. L., 2010. Influence of input motion and site property variabilities on seismic site response analysis. Journal of Geotechnical and Geoenvironmental Engineering, 136(4):607-619. doi: 10.1061/(ASCE)GT.1943-5606.0000255 U.S. Atomic Energy Commission, 1973. Regulatory guide 1.60:design response spectra for seismic design of nuclear power plants. Washington, DC, USA:U.S. Atomic Energy Commission. -
下载:
点击查看大图
计量
- 文章访问数: 107
- HTML全文浏览量: 18
- PDF下载量: 19
- 被引次数: 0
