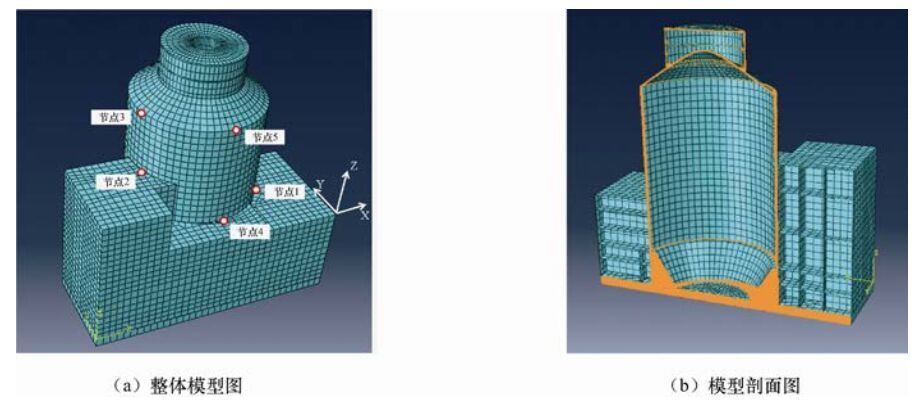
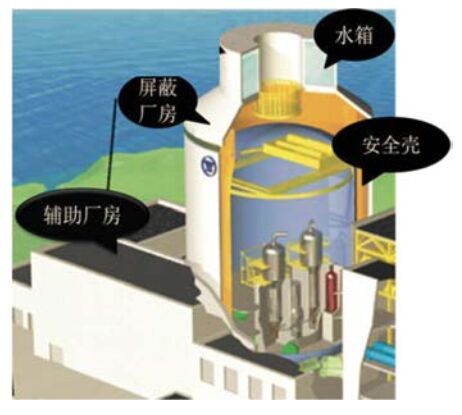
The Seismic Response Effect Analysis of Scaled Models of CAP1400 Nuclear Island Structure
-
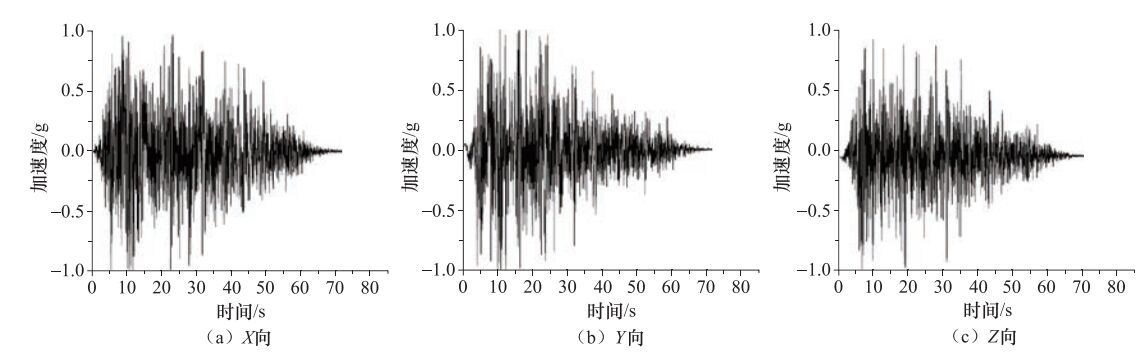
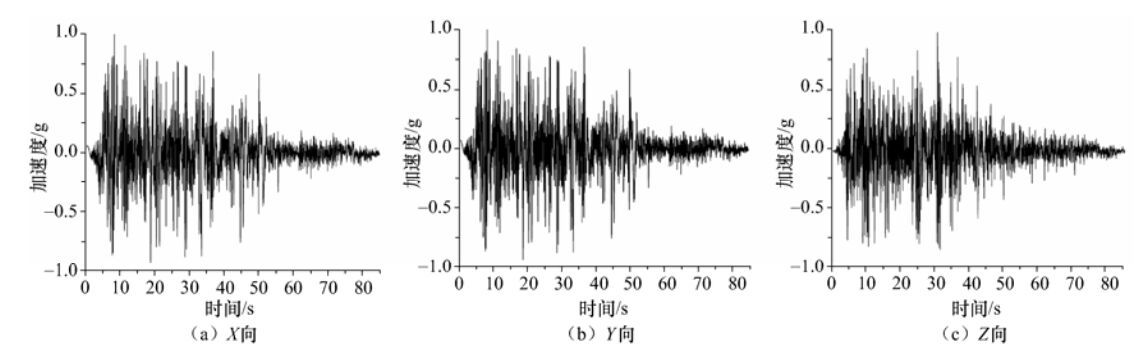
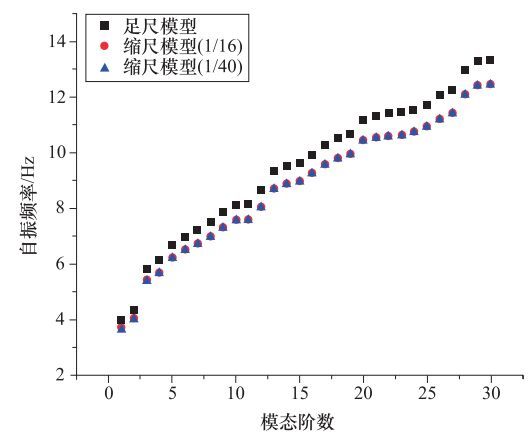
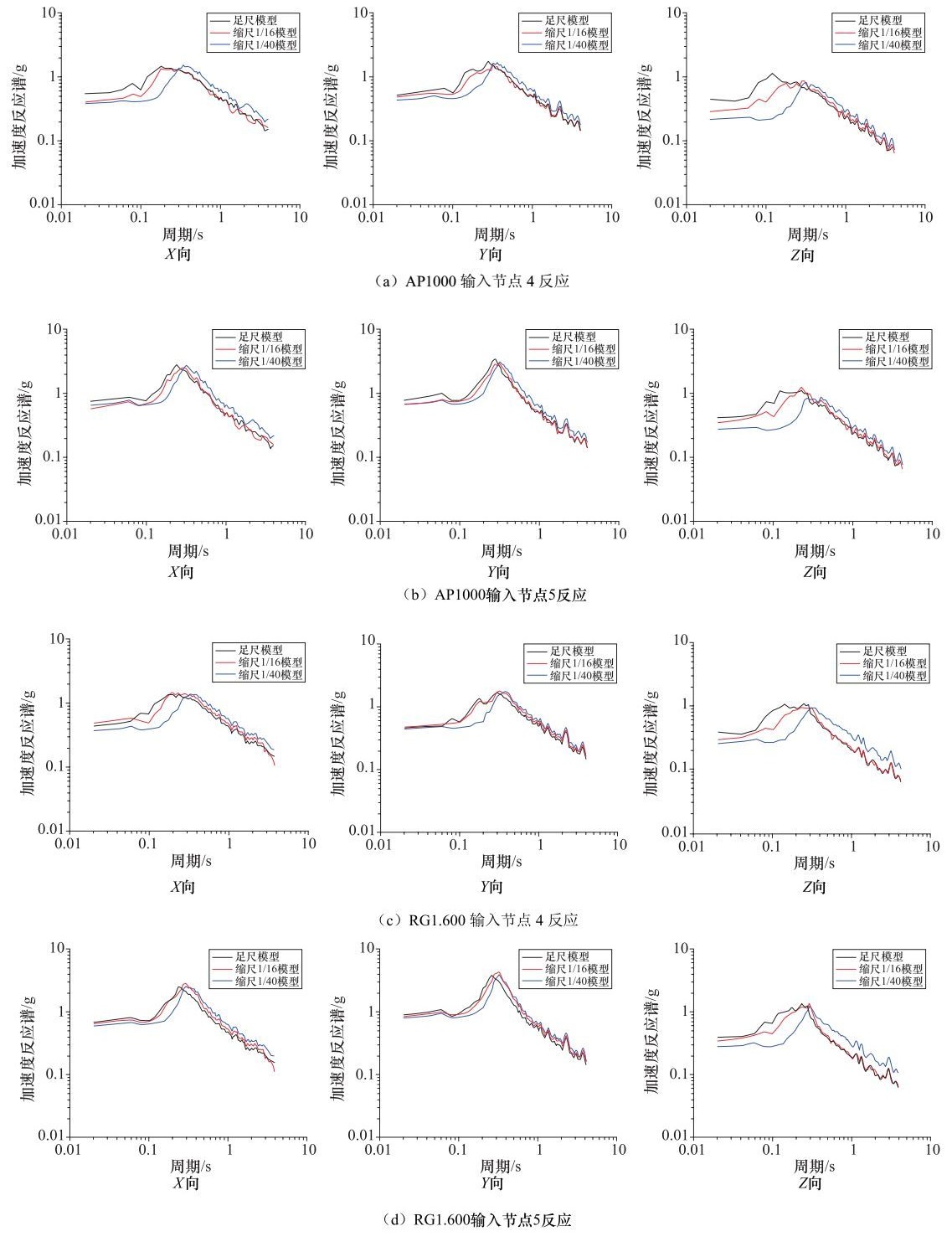
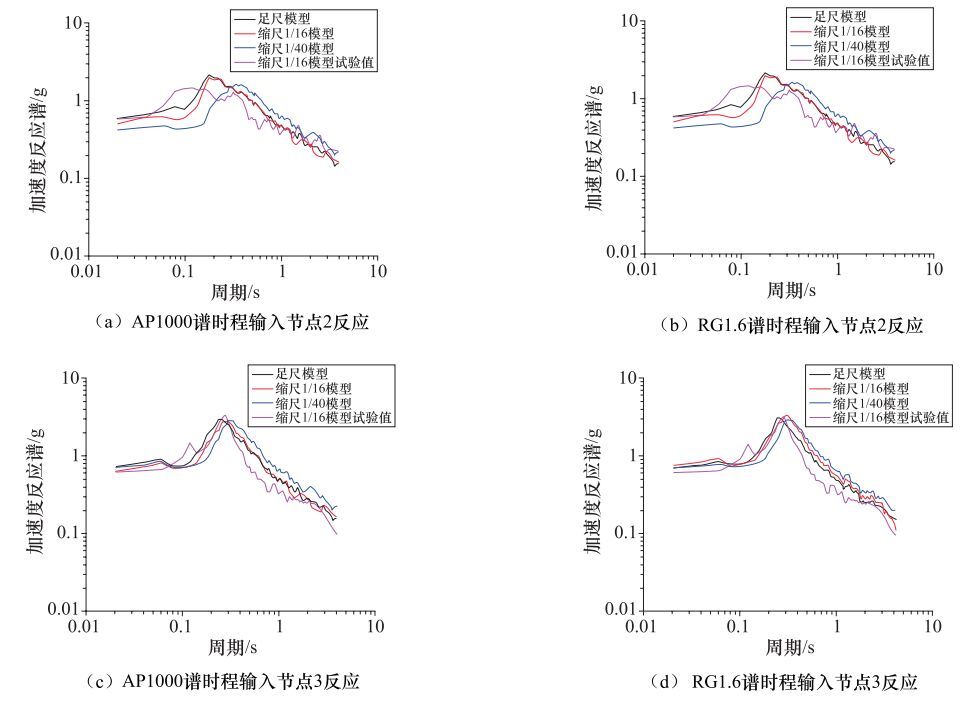
摘要: 针对核电厂CAP1400核岛结构地震反应问题，构建了核岛屏蔽厂房和辅助厂房整体结构的3个分析模型：原型和1/16、1/40缩尺模型，并在AP000谱和RG1.60谱地震动输入下进行了有限元模拟对比分析，探讨了振动台试验模型缩尺处理的合理性和精确性。研究表明，基于缩尺模型得到的结构自振频率相对于原型结构模型有所降低，降低幅度在8.5%以内；结构模型的缩尺对结构反应峰值加速度和高频（大于3Hz）加速度反应谱的影响较为显著，但对较低频（小于3Hz）的加速度反应谱影响较小；模型缩尺对结构不同方向反应的影响中，刚度越大的方向其影响越大。进一步将结构模型数值模拟结果与1/16缩尺模型的振动台试验结果进行了比较分析，试验给出的结构自振频率远低于模型数值模拟结果，但原型和1/16缩尺模型数值模拟得到的结构反应均与试验结果较为接近。基于模型数值模拟和振动台试验研究，认为对于缩尺比1/16或更大的模型可以忽略模型的缩尺效应。Abstract: Aiming at the seismic response problem of CAP1400 nuclear island structure of the nuclear power plant 3 analytical models, prototype and 1/16, 1/40 scale models, were constructed for the whole structure of the shielding and auxiliary factory, and comparative analysis of the seismic responses of the 3 models was done by finite element method under the ground motions matching AP000 spectrum and the RG1.60 spectrum, the rationality and accuracy were discussed on the scaled model for the shaking table testing. The research shown that natural frequencies of structure response from scaled models are smaller than that produced in the prototype structure model, the reduction was within 8.5%; the effect of scaled models is obviously on the peak acceleration and high frequency (more than 3Hz) spectral accelerations of structure response, but less on the low frequency (less than 3Hz) spectral accelerations; the effect of scaled model on the structure response is larger in direction of larger stiffness. In addition, the contrastive analysis between numerical simulation of different scale models and a shaking table testing of 1/16 scale model was carried out, which indicates that the natural frequencies from the shaking table testing is far lower than those from numerical simulation, but the simulated structure responses of the prototype and 1/16 scale models and the test results of 1/16 scale model were relatively close. The study reveals that scale effect of analysis and testing models can be ignored for scaled models of 1/16 or greater.
-
Key words:
- Nuclear power plant /
- Scaled model /
- Numerical analysis /
- Shaking table test /
- Spectral acceleration
-
图 1 CAP1400核岛结构屏蔽厂房与辅助厂房示意图
Figure 1. A diagram of the shielding and auxiliary factory structure of nuclear power plant CAP1400
图 2 CAP1400核岛结构有限元模型
Figure 2. The finite element model of nuclear power plant CAP1400 structure
图 4 AP1000谱人工地震动加速度时程
Figure 4. Artificial acceleration time-history corresponding to AP1000 spectra
图 5 RG1.60谱人工地震动加速度时程
Figure 5. Artificial acceleration time-history corresponding to RG1.60 spectra
图 6 不同缩尺比模型计算得到的结构反应前30阶自振频率
Figure 6. The first 30 natural frequencies of structure response from different scale structure models
图 7 制控节点处结构反应峰值加速度放大系数
Figure 7. Peak acceleration amplification factor of structural response at control points
图 8 控制性节点处结构反应加速度反应谱（一）
Figure 8. Spectral accelerations of structural response at control points
图 8 控制性节点处结构反应加速度反应谱（二）
Figure 8. Spectral accelerations of structural response at control points
图 9 结构反应加速度反应谱的数值计算结果与试验结果的比较
Figure 9. Comparison of spectral accelerations between the numerical analysis and model testing
表 1 核岛结构缩尺模型设计相似关系
Table 1. Similitude relation of scaled models of nuclear power plant structure
物理量 量纲 相似系数（1/16模型） 相似系数（1/40模型） 尺寸L [L] 1/16 1/40 线位移δ [L] 1/16 1/40 角位移β 1 1 弹性模量E [FL-2] 0.340 0.233 密度ρ [FL-4T2] 1 1 泊松比μ 1 1 应变ε 1 1 应力σ [FL-2] 0.340 0.233 等效质量密度ρε [FL-4T2] 1.74 1.74 集中荷载F [F] 1.328×10-3 1.458×10-4 弯矩M [FL] 8.300×10-5 3.645×10-6 时间t [T] 1.414×10-1 6.827×10-2 自振频率ω [T-1] 7.072 14.647 阻尼比ξ 1 1 加速度幅值ɑ [LT-2] 3.126 5.363 加速度频率υ [T-1] 7.072 14.647 结构刚度k [FL-1] 2.125×10-2 5.832×10-3 结构自重m [FL-1T2] 4.248×10-4 2.719×10-5 
下载: 导出CSV
表 2 不同缩尺比模型计算得到的结构反应前4阶自振频率
Table 2. The first 4 natural frequencies of structure response from different scaled structure models
振型序号 1 2 3 4 1/1模型自振频率/Hz 3.99 4.35 5.82 6.14 1/16模型自振频率 计算值/Hz 26.34 28.70 38.38 40.60 反推值/Hz 3.72 4.05 5.42 5.74 与1/1模型的相对误差/% -6.77 -6.90 -6.70 -6.51 1/40模型自振频率 计算值/Hz 53.49 58.88 79.18 83.41 反推值/Hz 3.65 4.02 5.41 5.69 与1/1模型的相对误差/% -8.52 -7.59 -7.04 -7.33
下载: 导出CSV
表 3 控制性节点处结构反应的峰值加速度（单位：g）
Table 3. Peak accelerations of structural response at the control points
节点 输入地震动：AP1000时程 输入地震动：RG1.60时程 缩尺比 1/1 1/16 1/40 缩尺比 1/1 1/16 1/40 1 X向 0.489 0.474（-3.1） 0.351（-28.2） X向 0.539 0.526（-2.4） 0.359（-33.3） Y向 0.482 0.481（-2.1） 0.408（-15.3） Y向 0.500 0.470（-6.0） 0.388（-22.4） Z向 0.386 0.292（-24.4） 0.220（-43.0） Z向 0.376 0.306（-18.6） 0.258（-31.4） 2 X向 0.546 0.54（-1.1） 0.478（-12.5） X向 0.574 0.652（13.6） 0.449（-21.8） Y向 0.561 0.596（6.2） 0.554（-1.2） Y向 0.522 0.562（7.7） 0.540（34.5） Z向 0.378 0.298（-21.2） 0.248（-34.4） Z向 0.348 0.301（-13.5） 0.258（-25.8） 3 X向 0.756 0.569（-24.7） 0.652（-13.8） X向 0.770 0.817（6.1） 0.704（-8.6） Y向 0.817 0.708（-13.3） 0.717（-12.2） Y向 0.789 0.704（-10.8） 0.737（-6.6） Z向 0.396 0.328（-17.2） 0.267（-32.6） Z向 0.410 0.354（-13.7） 0.264（-35.6） 4 X向 0.511 0.380（-25.6） 0.378（-26.0） X向 0.420 0.504（20.0） 0.386（-8.1） Y向 0.520 0.486（-6.5） 0.444（-14.6） Y向 0.448 0.464（35.7） 0.435（-2.9） Z向 0.414 0.292（-29.5） 0.223（-46.1） Z向 0.348 0.283（-18.7） 0.257（-26.1） 5 X向 0.554 0.520（-6.1） 0.565（19.9） X向 0.659 0.642（-2.6） 0.595（-9.7） Y向 0.920 0.830（-9.8） 0.789（-14.2） Y向 0.897 0.850（-5.2） 0.811（-9.6） Z向 0.381 0.328（-13.9） 0.242（-36.5） Z向 0.402 0.346（-13.9） 0.289（-28.1）
下载: 导出CSV
-
蔡新江, 田石柱, 2011.振动台试验方法的研究进展.结构工程师, 27(S):42-46. http://www.cnki.com.cn/Article/CJFDTOTAL-JGGC2011S1010.htm 杜修力, 韩俊艳, 李立云, 2013.长输埋地管道振动台试验设计中相似关系的选取.防灾减灾工程学报, 33(3):246-252. http://www.cnki.com.cn/Article/CJFDTOTAL-DZXK201303003.htm 侯春林, 李小军, 潘蓉等, 2016.地震动持时对核岛结构设计地基场地非线性地震响应影响分析.工业建筑, 46(10):9-12, 21. http://www.cnki.com.cn/Article/CJFDTOTAL-GYJZ201610003.htm 黄思凝, 郭迅, 孟庆利等, 2013.地震模拟试验中单质点体系小比例尺模型的分级相似关系.应用基础与工程科学学报, 21(1):71-77. http://www.cnki.com.cn/Article/CJFDTOTAL-YJGX201301009.htm 姜忻良, 徐炳伟, 李竹, 2010.土-桩-结构振动台模型试验相似理论及其实施.振动工程学报, 23(2):225-229. http://www.cnki.com.cn/Article/CJFDTOTAL-ZDGC201002016.htm 李勇, 闫维明, 刘晶波等, 2013.桥梁结构缩尺模型模拟地震振动台试验研究进展.工程抗震与加固改造, 35(5):1-10. http://www.cnki.com.cn/Article/CJFDTOTAL-GCKZ201305001.htm 李振宝, 李晓亮, 唐贞云等, 2010.土-结构动力相互作用的振动台试验研究综述.震灾防御技术, 5(4):439-450. doi: 10.11899/zzfy20100406 林皋, 2011.核电工程结构抗震设计研究综述(Ⅰ).人民长江, 42(19):1-6. doi: 10.3969/j.issn.1001-4179.2011.19.001 柳春光, 孙国帅, 韩亮等, 2012.桥梁水下桩墩结构振动台模型试验相似律验证.地震工程与工程振动, 32(4):13-18. http://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201204003.htm 刘红彪, 李宏男, 2016.地震模拟振动台试验模型相似设计中的材料弹性模量取值问题研究.振动与冲击, 35(3):114-120. http://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201603019.htm 吕西林, 沈德建, 2008.不同比例钢-混凝土混合结构高层建筑动力相似关系试验研究.地震工程与工程振动, 28(4):50-57. http://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200804008.htm 孟庆利, 黄思凝, 郭迅, 2008.钢筋混凝土结构小比例尺模型的相似性研究.世界地震工程, 24(4):1-6. http://cdmd.cnki.com.cn/Article/CDMD-85406-2009057338.htm 钱德玲, 李元鹏, 刘杰, 2013.高层建筑结构振动台模型试验与原型对比的研究.振动工程学报, 26(3):436-442. http://www.cnki.com.cn/Article/CJFDTOTAL-ZDGC201303019.htm 权登州, 王毅红, 井彦林等, 2015.黄土地区地铁车站数值模型及测试位置研究.震灾防御技术, 10(1):108-115. doi: 10.11899/zzfy20150111 宋二祥, 武思宇, 王宗纲, 2008.地基-结构系统振动台模型试验中相似比的实现问题探讨.土木工程学报, 41(10):87-92. doi: 10.3321/j.issn:1000-131X.2008.10.013 杨树标, 李荣华, 刘建平等, 2007.振动台试验模型和原型相似关系的理论研究.河北工程大学学报(自然科学板), 24(1):8-11. http://www.cnki.com.cn/Article/CJFDTOTAL-HJXU200701002.htm 杨树标, 杜广辉, 李荣华等, 2008.结构动力模型相似关系研究及验证.河北工程大学学报(自然科学板), 25(3):4-7. http://www.cnki.com.cn/Article/CJFDTOTAL-HJXU200803001.htm 张佳, 王毅红, 权登州等, 2016.黄土地区地铁地下车站地震变形特性研究.震灾防御技术, 11 (2):272-282. doi: 10.11899/zzfy20160210 张敏政, 1997.地震模拟实验中相似律应用的若干问题.地震工程与工程振动, 17(2):52-58. http://www.cnki.com.cn/Article/CJFDTOTAL-DGGC702.006.htm 赵作周, 管桦, 钱稼茹, 2010.欠人工质量缩尺振动台试验结构模型设计方法.建筑结构学报, 31 (7):78-85. http://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201007013.htm 郑升宝, 蒋树屏, 王晓雯等, 2010.隧道振动台模型试验的相似关系.重庆交通大学学报(自然科学板), 29(6):875-879. http://www.cnki.com.cn/Article/CJFDTOTAL-CQJT201006011.htm 周颖, 吕西林, 卢文胜, 2006.不同结构的振动台试验模型等效设计方法.结构工程师, 22(4):37-40. http://www.cnki.com.cn/Article/CJFDTOTAL-JGGC200604008.htm Dai Z. J., Li X. J., Hou C. L., 2014. An optimization method for the generation of ground motions compatible with multi-damping design spectra. Soil Dynamics and Earthquake Engineering, 66:199-205. doi: 10.1016/j.soildyn.2014.06.032 Paolucci R., Shirato M., Yilmaz M. T., 2008. Seismic behaviour of shallow foundations:shaking table experiments vs numerical modelling. Earthquake Engineering & Structural Dynamics, 37(4):577-595. doi: 10.1002/eqe.773 Pitilakis D., Dietz M., Wood D. M., et al., 2008. Numerical simulation of dynamic soil-structure interaction in shaking table testing. Soil Dynamics and Earthquake Engineering, 28(6):453-467. doi: 10.1016/j.soildyn.2007.07.011 Severn R. T., 2011. The development of shaking tables-A historical note. Earthquake Engineering & Structural Dynamics, 40(2):195-213. doi: 10.1002/eqe.1015/epdf Shi T. H., Cheng S. G., 2013. Dynamic similitude law design of shaking table model test for high-rise steel structures. In:5th International Conference on Advances in Experimental Structural Engineering. Taipei, Taiwan:NCREE. Žarnić R., Gostič S., Crewe A. J., et al., 2001. Shaking table tests of 1:4 reduced-scale models of masonry infilled reinforced concrete frame buildings. Earthquake Engineering & Structural Dynamics, 30(6):819-834. -
点击查看大图
计量
- 文章访问数: 92
- HTML全文浏览量: 5
- PDF下载量: 22
- 被引次数: 0
