The Influence of Surface Wave Condition on Hydrodynamic Pressures of Seawater under Earthquake and Waves
-
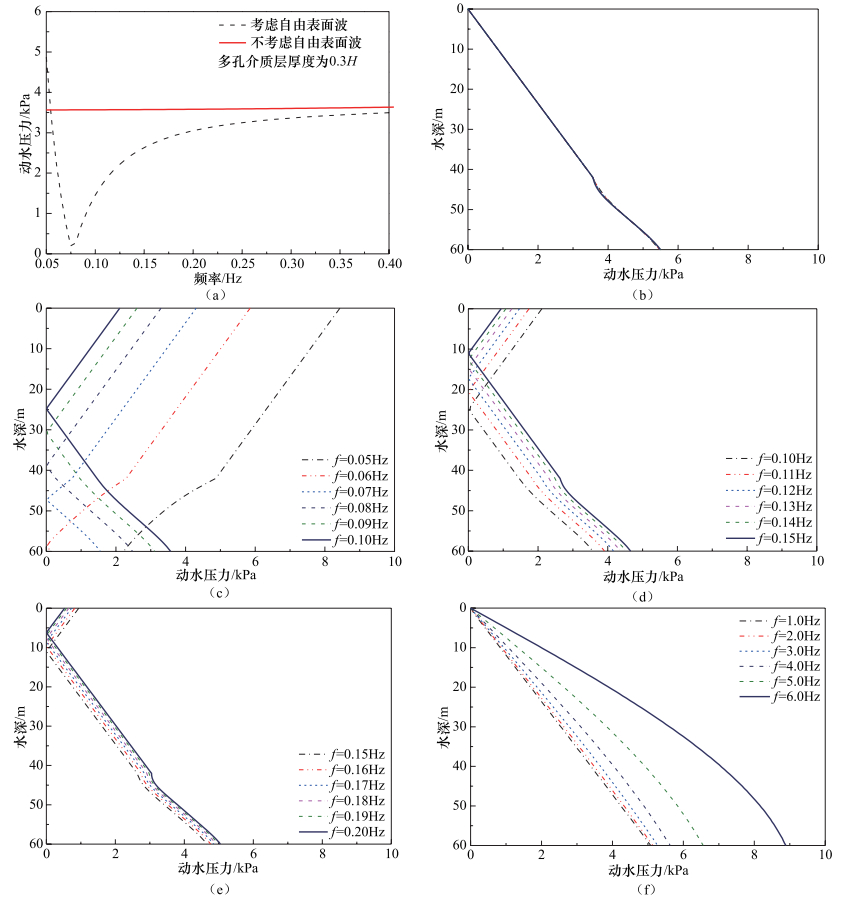
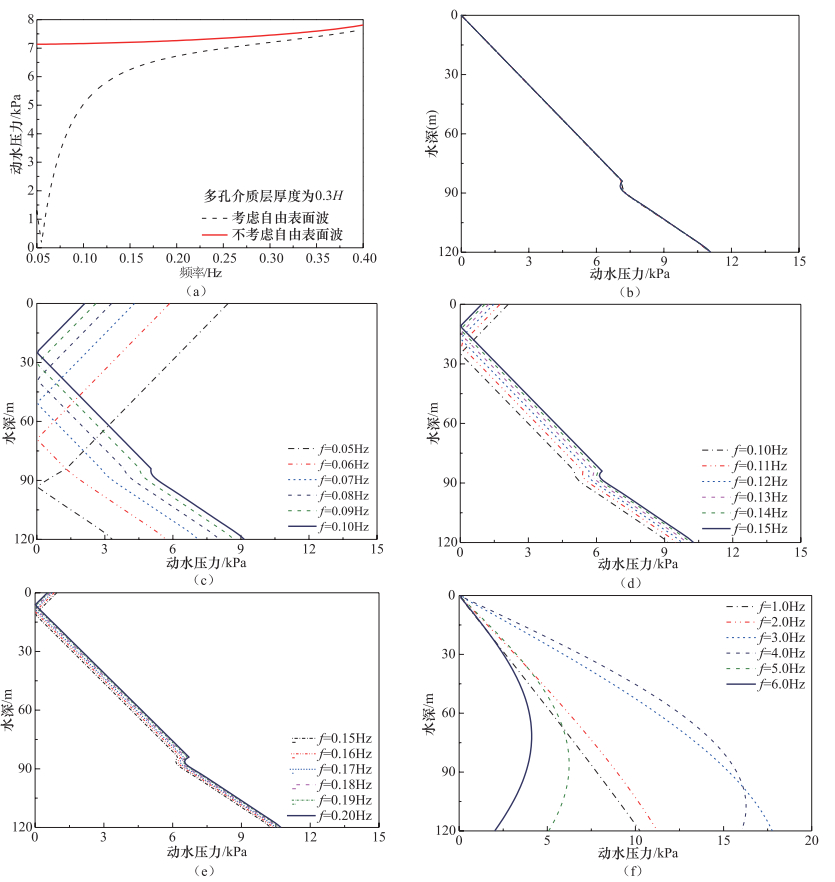
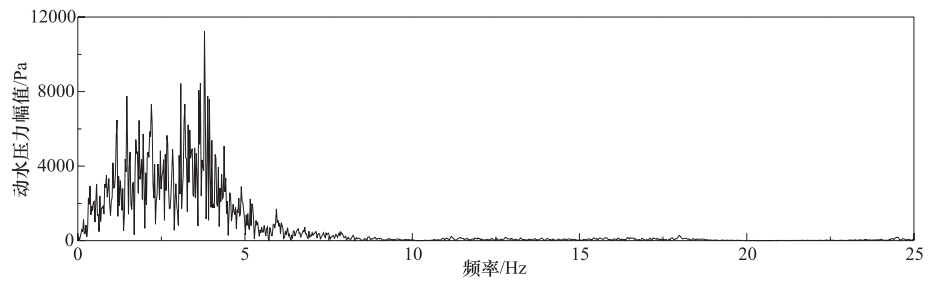
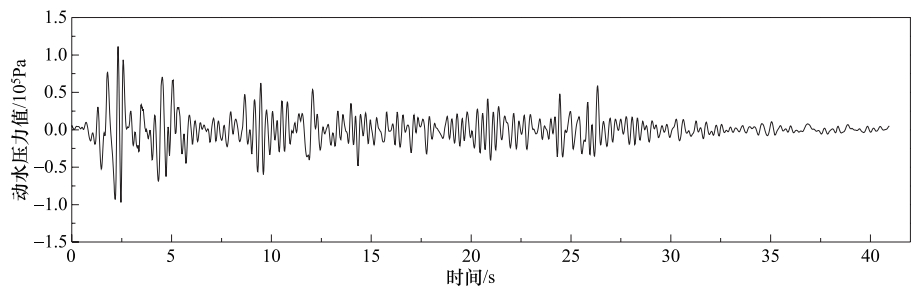
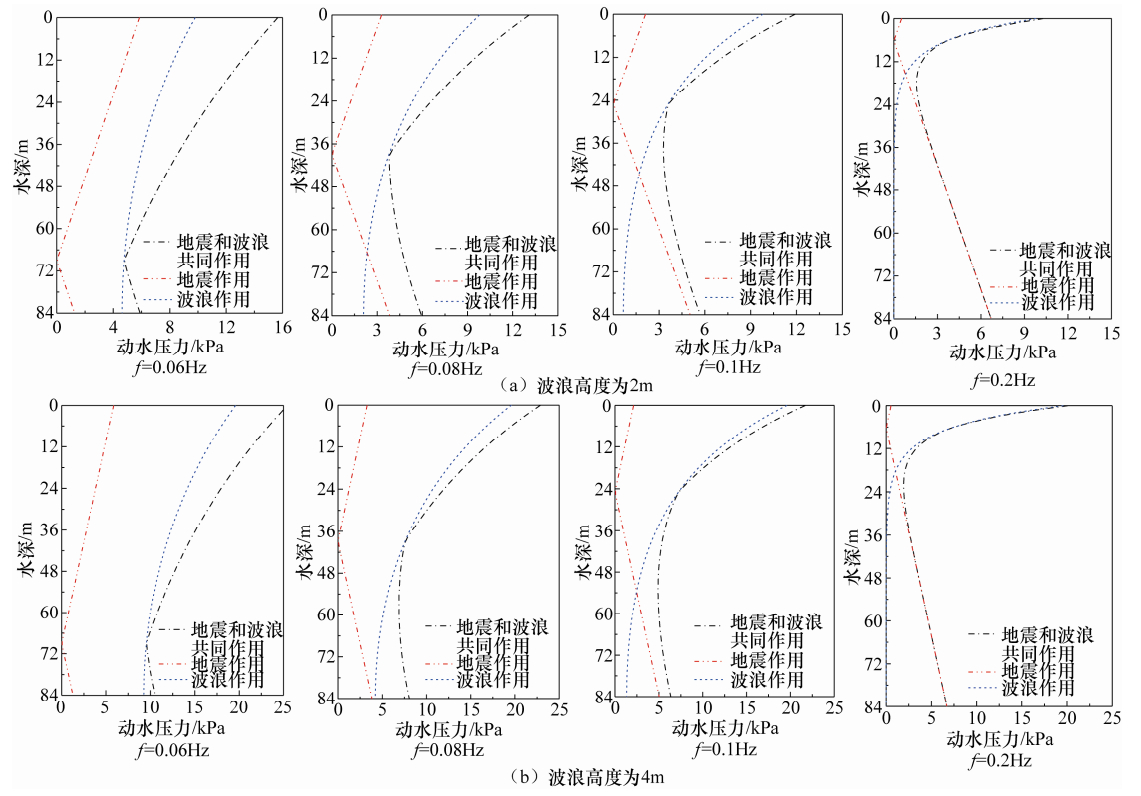
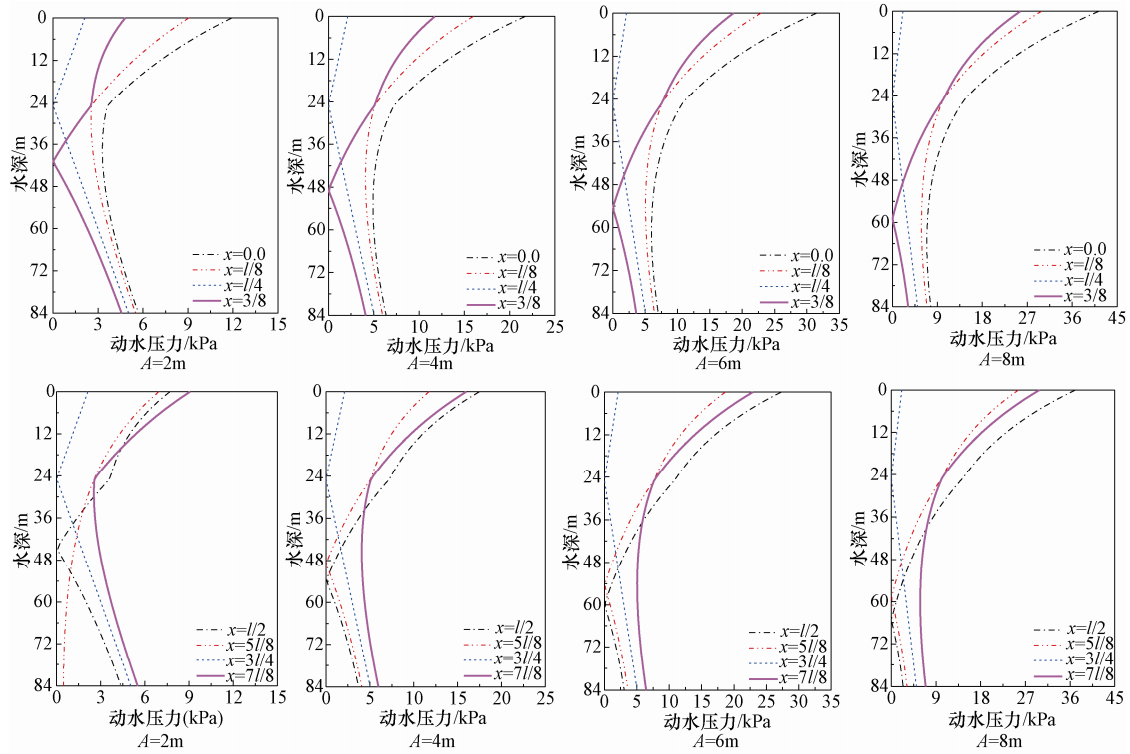
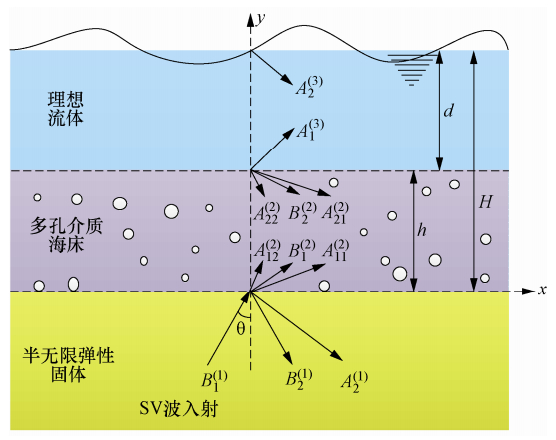
摘要: 地震动斜入射条件下海洋场地简化为理想流体海水-两相介质海床-弹性固体基岩系统模型，通常假定为静水液面条件。本文以地震动SV波为例，推导了表面波条件下海洋场地动力反应解析解，研究了表面波条件对海水动水压力的影响。研究表明，表面波频率在大于0.5Hz时对海水动水压力几乎无影响，在小于0.5Hz范围内有影响，且越接近水面、频率越低时影响越显著。实际地震动卓越频率通常大于0.5Hz，因而地震动作用下采用忽略表面波条件的静水液面假定是合理的。进一步结合线性波浪理论，研究SV波和波浪联合作用下表面波条件对海水动水压力的影响。研究表明，由于波浪属于低频荷载且频率通常小于0.5Hz，在地震和波浪联合作用下表面波条件的影响较地震单独作用更为显著。Abstract: The ocean site is usually simplified as the seawater-seabed-bedrock system under the obliquely incident earthquake, where the seawater is ideal fluid, the seabed is poroelastic media, and the bedrock is elastic solid. In this paper, the analytical solution to the dynamic responses of the ocean site with the surface wave condition is derived. The influence of the surface wave condition on the ground motion hydrodynamic pressures of seawater is studied. Our results show that when the frequency is higher than 0.5 Hz, the surface wave condition is almost no effect. If the frequency is lower than 0.5 Hz, the effect is significant. The closer to the surface position and the lower frequency will enhance such effect. Because the excellent frequency of actual ground motion is generally larger than 0.5 Hz, the assumption of the rest surface condition is reasonable. However, since the wave is low frequency load and its frequency usually is less than 0.5Hz, the effect of the surface wave condition is more significant under the action of earthquake and wave than under only earthquake.
-
Key words:
- Surface wave condition /
- Earthquake /
- Waves /
- Hydrodynamic pressure of seawater
-
引言
地震前兆观测主要关注观测数据随时间的相对变化，装置系数误差不影响观测数据的相对变化，但不正确的装置系数可能导致地电阻率观测结果出现系统误差（王兰炜等，2014），因此，正确的装置系数有利于不同区域观测数据的对比和地震前兆数据的研究。自2009年起，河北大柏舍台，甘肃天水台、武都台、平凉台，陕西合阳台实施了井下地电阻率垂直观测试验，井孔深100—225m，供电极距60—120m，测量极距20—60m（刘君等，2015；王兰炜等，2015）。上述台站地电阻率垂向观测通常为1个钻孔，供电电极和测量电极均布设于1个钻孔中，部分垂向观测的供电电极A接近地表，如天水台、武都台、合阳台的供电电极A埋深仅4—5m；部分垂向观测的供电电极A埋深为40m左右，如大柏舍台。垂向地电阻率观测中的装置系数与电流的空间分布及电极位置有关，现有垂向观测装置系数计算方法依据地下点、地表点电流源产生的电场计算得出，忽略了供电电极A的埋深。江宁台深井垂向地电阻率观测装置为在2口深井进行垂向观测的试验装置，与传统垂向地电阻率观测装置不同。本文根据地下点电流源产生的电场讨论装置系数计算方法，并比较计算方法对江宁台垂向地电阻率观测的影响。
1. 台址概况
江宁台地处南京市江宁区禄口街道水荆墅村，地形开阔平坦，周围无大中型工矿企业，测区位于南京-湖熟断裂南西盘和方山-小丹阳断裂西盘的楔形地块上，东距茅山断裂带30km，西北距长江36km。测区内现有垂向地电阻率观测装置为在2口深井进行垂向观测的试验装置，井距5.17m，供电电极A、测量电极M分别布设在深275m的2号井内200m和275m处，供电电极B、测量电极N分别布设在深400m的1号井内400m和325m处（图 1）。该垂向观测系统采用ZD8BI型地电仪，根据《地震台站建设规范（地电台站第1部分）》（DB/T.18.1—2006）中关于地电阻率台站的技术要求，对新建垂向观测装置的场地进行高密度电法、电测深等测试。高密度电法探测和电测深报告中NW—SE和NS测线结果表明，观测区域电测深曲线具有K形特征，电性结构等效为3层（樊晓春等，2018），场地电性层参数见表 1。
表 1 江宁台场地电性层参数Table 1. The underground electrical structure of Jiangning geoelectric stationNW—SE测线 NS测线 层厚/m 电阻率/Ω·m 层厚/m 电阻率/Ω·m 29.40 39.29 24.56 18.71 220.94 143.06 203.42 274.52 ∞ 60.39 ∞ 54.79 2. 点电流源在非全空间产生的电场
点电流处于不完全全空间时，对点电流源位于地下和地表 2种情况进行讨论。地下点电流源产生的电场指点电流源的电流I在地下一定深度时流入地下介质中产生的电场，为不完全全空间。假设地下介质电性均匀，介质电阻率为ρ，电流I从地下A点流入（图 2），采用镜像法计算（刘昌谋等，1994；刘国兴，2005），见式（1）。地表点电流源产生的电场指地表点电流源电流I流入地下介质，从无限远处流出时在介质中产生的电场，为半无限空间。假设地下介质电性均匀，介质电阻率为ρ，电流I从地表A点流入地下，电流线的分布以A为中心向周围呈辐射状，该情况为图 2的特例（王兰炜等，2014），见式（2）。
图 2 地下点电源产生的电场示意图Figure 2. The schematic diagram of the electric field generated by underground point power supply（1）地下点电流源产生的电场（不完全全空间）
$$ {V_{{\rm{MN}}}} = \frac{{\rho I}}{{4{\rm{ \mathsf{ π} }}}}\left({\frac{1}{{\overline {AM} }} + \frac{1}{{\overline {{A_1}M} }} - \frac{1}{{\overline {{A_1}N} }} - \frac{1}{{\overline {AN} }}} \right) $$ (1) （2）地表点电流源产生的电场（半无限空间）
$$ {V_{{\rm{MN}}}} = \frac{{\rho I}}{{2{\rm{ \mathsf{ π} }}}}\left({\frac{1}{{\overline {AM} }} - \frac{1}{{\overline {AN} }}} \right) $$ (2) 3. 装置系数计算方法
装置系数是地电阻率观测中特有的参数，通常用K表示，与观测装置中电极分布情况有关，表征地电阻率是视电阻率（王兰炜等，2014）。当测区区域介质电阻率均匀分布时，地电阻率ρs与介质真实的电阻率ρ数值相同。
根据奥斯定理和镜像原理（钱家栋等，1985），假设测区为均匀介质，垂向观测中的装置系数计算方法如下：
（1）方法Ⅰ：传统垂向观测装置系数计算方法（王兰炜等，2014）
传统方法井下垂向观测装置忽略电极A的埋深，在点电源B与地面对称的位置设镜像点B1，见图 3（a）。根据式（1）和式（2），则K为：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\left({\frac{2}{{\overline {AM} }} - \frac{2}{{\overline {AN} }}} \right) - \left({\frac{1}{{\overline {BM} }} + \frac{1}{{\overline {{B_1}M} }} - \frac{1}{{\overline {{B_1}N} }} - \frac{1}{{\overline {BN} }}} \right)}} $$ (3) 不考虑江宁台垂向观测电极A埋深时，因江宁台垂向观测AM=BN，AN=BM，则：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\frac{3}{{\overline {AM} }} - \frac{3}{{\overline {AN} }} - \frac{1}{{\overline {{B_1}M} }} + \frac{1}{{\overline {{B_1}N} }}}} $$ (4) （2）方法Ⅱ：采用全空间方式的装置系数计算方法（钱家栋等，1985；王兰炜等，2014）
当电极埋深h远大于供电极长度AB时，为全空间，则K为地表观测装置系数的2倍，即：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\frac{1}{{\overline {AM} }} - \frac{1}{{\overline {AN} }} - \frac{1}{{\overline {BM} }} + \frac{1}{{\overline {BN} }}}} $$ (5) （3）方法Ⅲ：采用不完全全空间方式的装置系数计算方法
江宁台垂向观测的电极A、M、N、B分别位于埋深200m、275m、325m、400m处，应按地下点电源产生的电场模型计算（不完全全空间），如图 3（b）所示。在点电源A、B与地面对称的位置设镜像点A1、B1，忽略1号井和2号井的水平距离l，根据式（1），则供电电流I（+I和-I）在M、N间产生的电位差为：
$$ {V_{MN}} = \frac{{\rho I}}{{4{\rm{ \mathsf{ π} }}}}\left[ {\left({\frac{1}{{\overline {AM} }} + \frac{1}{{\overline {{A_1}M} }} - \frac{1}{{\overline {{A_1}N} }} - \frac{1}{{\overline {AN} }}} \right) - \left({\frac{1}{{\overline {BM} }} + \frac{1}{{\overline {{B_1}M} }} - \frac{1}{{\overline {{B_1}N} }} - \frac{1}{{\overline {BN} }}} \right)} \right] $$ (6) 则K为：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\left({\frac{1}{{\overline {AM} }} + \frac{1}{{\overline {{A_1}M} }} - \frac{1}{{\overline {AN} }} - \frac{1}{{\overline {{A_1}N} }}} \right) - \left({\frac{1}{{\overline {BM} }} + \frac{1}{{\overline {{B_1}M} }} - \frac{1}{{\overline {BN} }} - \frac{1}{{\overline {{B_1}N} }}} \right)}} $$ (7) 因江宁台垂向观测AM=BN，AN=BM，则：
$$ K = \frac{{4{\rm{ \mathsf{ π} }}}}{{\frac{2}{{\overline {AM} }} - \frac{2}{{\overline {AN} }} + \frac{1}{{\overline {{A_1}M} }} - \frac{1}{{\overline {{A_1}N} }} - \frac{1}{{\overline {{B_1}M} }} + \frac{1}{{\overline {{B_1}N} }}}} $$ (8) （4）方法Ⅳ：采用不完全全空间方式（考虑井距l）的装置系数计算方法
按照地下点电源产生电场的模型计算（不完全全空间），在点电源A、B与地面对称的位置设镜像点A1、B1，h1、h2、h3表示供电电极A、B、M的电极埋深，井距l表示2口井孔水平距离（图 3（c）），则：
$$ \overline {AM} = {h_3} - {h_1} $$ (9) $$ \overline {AN} = \sqrt {{l^2} + {{({h_2} - {h_3})}^2}} $$ (10) $$ \overline {{A_1}M} = {h_1} + {h_3} $$ (11) $$ \overline {{A_1}N} = \sqrt {{l^2} + {{({h_2} + 2{h_1} - {h_3})}^2}} $$ (12) $$ \overline {{B_1}M} = \sqrt {{l^2} + {{({h_2} + {h_3})}^2}} $$ (13) $$ \overline {{B_1}N} = 2{h_2} - {h_3} + {h_1} $$ (14) 将式（9）至式（14）代入式（8），则K变为：
$$ K = \frac{{4\pi }}{{\frac{2}{{{h_3} - {h_1}}} - \frac{2}{{\sqrt {{l^2} + {{({h_2} - {h_3})}^2}} }} + \frac{1}{{{h_1} + {h_3}}} - \frac{1}{{\sqrt {{l^2} + {{({h_2} + 2{h_1} - {h_3})}^2}} }} - \frac{1}{{\sqrt {{l^2} + {{({h_2} + {h_3})}^2}} }} + \frac{1}{{2{h_2} - {h_3} + {h_1}}}}} $$ (15) 4. 江宁台垂向地电阻率观测装置系数计算
采用方法Ⅰ—Ⅳ分别计算江宁台垂向地电阻率观测的装置系数K，结果见表 2。考虑江宁台垂向地电阻率观测的电极布设不同于传统垂向观测装置，所有电极埋深均在200m以上，本文认为应以方法Ⅳ为参考值，采用式（16）计算不同装置系数计算方法的相对误差。方法Ⅰ、Ⅱ、Ⅲ相对误差分别为-32.01%、1.37%、0.43%，可知方法Ⅰ不适用于江宁台垂向地电阻率观测，该计算方法通常仅适用于供电电极A埋深小于5m的垂向观测，如天水台、合阳台。方法Ⅱ相对误差较小，江宁台垂向观测于2018年4月25日至2018年11月22日曾采用该方法。考虑仅当电极埋深远大于供电极距时称为全空间，而江宁台垂向装置最小电极埋深仅与供电极距相当，因此，方法Ⅱ同样不适用于江宁台垂向观测。除江宁台外，大部分台站观测装置电极埋深明显小于供电极距，均不宜采用方法Ⅱ。方法Ⅲ相对误差最小，江宁台垂向地电阻率观测于2018年11月23日至2019年10月30日曾采用该方法，2018年11月出现的台阶是由调整装置系数导致的（图 4）。由于江宁台垂向地电阻率观测为多孔观测，须考虑井距才能准确计算其装置系数，因而最终采用方法Ⅳ进行计算。
$$ \sigma = \frac{{k_{方法}} - {k_{方法Ⅳ}}}{{{k_{方法Ⅳ}}}} $$ (16) 表 2 江宁台垂向观测的装置系数Table 2. The configuration coefficient of vertical geo-resistivity observation in Jiangning earthquake station计算方法 AM/m AN/m B1M/m B1N/m A1M/m A1N/m 装置系数K Ⅰ 75.000 125.000 675.000 725.000 — — 790.000 Ⅱ 75.000 125.000 — — — — 1178.000 Ⅲ 75.000 125.000 675.000 725.000 475.000 525.000 1167.000 Ⅳ 75.000 125.374 675.020 725.000 475.000 525.292 1162.000 
图 4 江宁台垂向观测整点值曲线Figure 4. The hourly observational value curves of vertical geo-resistivity observation at Jiangning Seismic Station5. 结论
本文以江宁台垂向地电阻率观测为例，提出2种以不完全全空间方式计算的新方法，并与现有垂向观测装置计算方法进行比较。研究结果表明，方法Ⅳ最符合江宁台垂向地电阻率观测装置。考虑方法Ⅳ中部分参数存在小数部分，认为保留小数点后三位能满足装置系数精度要求。方法Ⅳ除适用于2口井垂向观测装置外，同样适用于忽略井距时供电电极A埋深超过5m的单口井垂向观测装置。
致谢: 衷心感谢中国地震局地壳应力研究所王兰炜研究员对本文提出的建议和意见。 -
图 1 SV波斜入射下半无限弹性固体-多孔介质-理想流体系统海洋场地示意图
Figure 1. Ocean site as half-space elastic solid-poroelastic medium-ideal fluid system under obliquely incident earthquake
图 2 水深60m时地震作用下的动水压力
Figure 2. Hydrodynamic water pressure caused by earthquake (H=60m)
图 3 水深120m时地震作用下的动水压力
Figure 3. Hydrodynamic water pressure caused by earthquake (H=120m)
图 6 地震和波浪联合作用下的动水压力
Figure 6. The hydrodynamic pressures under the coaction of earthquake and waves
-
雷枝, 2014. 地震和波浪联合作用下自由场海水动水压力反应研究. 北京工业大学. 王进廷, 金峰, 张楚汉, 2003.位于弹性半空间上的理想流体层动力反应——平面P波入射.工程力学, 20(6):12-17. http://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200306002.htm 王进廷, 张楚汉, 金峰, 2004.位于弹性半空间上的理想流体层动力反应——平面SV波入射.工程力学, 21(1):15-20. http://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200401002.htm 王进廷, 张楚汉, 金峰, 2008.淤砂层模型对上层理想流体动力反应的影响——平面SV波入射.岩土力学, 29(9):2359-2364. http://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200809012.htm 王忠涛, 2008. 随机和非线性波浪作用下海床动力响应和液化分析. 大连: 大连理工大学. 郑东升, 2013.波浪和海床交互作用的多孔介质原理 (英文版).上海:上海交通大学出版社. 竺艳蓉, 1991.海洋工程波浪力学.天津:天津工业大学出版社. Wang J. T., Zhang C. H. and Jin F., 2004. Analytical solutions for dynamic pressures of coupling fluid-soild-porous medium due to P wave incidence. Earthquake Engineering and Engineering Vibration, 3(2):263-271. doi: 10.1007/BF02858240 Wang J. T., Zhang C. H. and Jin F., 2009. Analytical solutions for dynamic pressures of coupling fluid-porous medium-solid due to SV wave incidence. International Journal for Numerical and Analytical Methods in Geomechanics, 33(12):1467-1484. doi: 10.1002/nag.v33:12 -
下载:
下载:
点击查看大图
计量
- 文章访问数: 143
- HTML全文浏览量: 23
- PDF下载量: 5
- 被引次数: 0
