Study of Simplified Calculation Method for Seismic Settlement of Soft Soil Based on Triaxial Test
-
摘要: 本文通过对天津滨海新区典型软土的静、动力学试验，分析了软土残余应变的变化规律，提出了结合地区震陷经验系数的软土震陷简化计算方法，并利用1976年唐山7.8级地震中天津塘沽地区软土震陷观测资料对计算方法进行了验证。结果表明，本方法用于估算自由地表震陷量是可行的，对中小工程中软土震陷量的估算具有一定的参考价值。Abstract: Based on the static and dynamic mechanical test of soft soil in Tianjin, we analyzed change law of residual strain of soft soil. The estimation method based on static algorithm and empirical coefficient is developed to compute the seismic settlement of soft soil. By comparing the calculated results with the measured data in the 1976 Tangshan earthquake, we proved that this method is feasible. It can be used to estimate the seismic settlement of soft soil in small and middle scale engineering project.
-
Key words:
- Soft soil /
- Dynamic triaxial test /
- Residual stain /
- Calculation method
-
引言
桥梁是为保证道路的连续性而专门建造的人工构筑物，也是城市生命线工程中极其重要的一部分。随着我国国民经济的不断发展，桥梁已成为城市正常运行的不可或缺的建筑物。我国是多地震国家，地震的突发性和强破坏性，往往给我国城市桥梁带来巨大的损害。桥梁是城市生命线工程和城市交通系统的重要组成部分，在交通系统防震减灾工作中处于核心地位 (王东升等，2001)，如果桥梁在地震中受到严重的破坏，将会严重阻碍地震应急和灾区的救援，从而严重影响人们的生产生活和灾后的恢复重建工作。有效的桥梁震害预测可以提高城市综合抗震救灾能力，为城市抗震防灾规划提供科学依据，因此具有重要的现实意义。
国内外对桥梁震害预测的方法主要有4类 (王东升等，2001；2003；姜淑珍等，2004)：经验统计法 (包括久保庆三郎方法、日本土木工程学会方法、朱美珍方法、Buckle方法、回归统计法等)，规范校核法，Pushover (推覆分析) 法和大跨度桥梁定性与定量相结合的震害预测方法。庄丽等 (2007)基于VB语言和经验统计公式对青岛市桥梁做出了震害预测，并将该方法运用到青岛市地震应急指挥系统；柳春光等 (2008)将遗传算法和BP神经网络相结合，克服了BP神经网络容易陷入局部最优、运算速度慢等弱点，建立了遗传优化BP神经网络的桥梁震害预测方法；谭潇等 (2013)用支持向量机 (SVM) 原理建立了桥梁震害评估的SVM模型，同时也证明了SVM模型对桥梁震害的预测优于基于人工神经网的预测模型。本文充分利用粒子群算法和支持向量机的优点，借助Matlab软件和Libsvm工具箱，结合桥梁的震害影响因素，建立基于PSO-SVM的城市桥梁震害模型，使桥梁的震害预测方法更加完善和多元。
1. PSO的基本知识
1.1 粒子群算法的基本原理
粒子群算法 (Particle Swarm Optimization，PSO) 是一种结构简单、易于实现、通用的智能算法。通常粒子群 (田雨波，2104) 的数学描述为：假设在一个n维的搜索空 间中由m个粒子组成的种群，其中第i个粒子位置${x_i} = {({x_{i, 1}}, {x_{i, 2}}, \ldots, {x_{i, m}})^{\rm{T}}} $，其粒子速度${v_i} = {({v_{i, 1}}, {v_{i, 2}}, \ldots, {v_{i, n}})^{\rm{T}}}$。它的一个极值为${P_i} = {({p_{i, 1}}, {p_{i, 2}}, \ldots, {p_{i, n}})^{\rm{T}}}$，种群的全局极值为${P_{\rm{g}}} = {({p_{{\rm{g}}, 1}}, {p_{{\rm{g}}, 2}}, \ldots, {p_{{\rm{g}}, n}})^{\rm{T}}}$。粒子群算法在找到以上的2个极值后，根据公式 (1) 和 (2) 不断更新自己的速度和位置：
$$ v_{i, d}^{k + 1} = v_{i, d}^k + {c_1} \cdot \;{r_1} \cdot \;(p_{i, d}^k - x_{i, d}^k) + {c_2} \cdot {r_2} \cdot \;(p_{g, d}^k - x_{i, d}^k) $$ (1) $$ x_{i, d}^{k + 1} = x_{i, d}^k + v_{i, d}^{k + 1} $$ (2) 其中，c1和c2常被称为学习因子或加速常数；r1、r2为介于0和1之间的随机数；$v_{i, d}^k$和$x_{i, d}^k$是粒子在第k次迭代中第d维的速度和位置；$p_{i, d}^k$是粒子在第k次迭代中第d维的个体极值的位置；与个体极值相对应的$p_{g, d}^k$是群体在第k次迭代中第d维的全局极值的位置。
1.2 粒子群的优化及其SVM的参数设置
支持向量机 (Support Vector Machine，SVM) 在解决小样本和非线性高维模式识别中具有明显优势。一个非线性的SVM模型主要通过把原始空间的低维非线性数据映射到高维空间，将其转化为线性可分问题 (王建国等，2015)，这样在高维的空间中就对应其低维的非线性回归问题，其本质就是在训练样本中来寻找一个最优超平面，是一个二次规划问题，可以通过对偶问题来求解。
其具体的步骤是通过一定的映射关系φ(·)，在一定的条件下构成核函数$K({x_i}, {x_j}) = (\varphi ({x_i}) \cdot \varphi ({x_j}))$以避免高维空间的复杂计算。设样本集 (王雪刚，2014；王书舟，2009)：$\{ (xi, yi), i = 1, 2, \cdots, l, xi \in {R^n}, yi \in R\} $，R为欧式空间，n为样本输入维数，对于引入松弛因子${\xi _i}、{\zeta _i}$的二次优化问题：
$$ \min [\frac{1}{2}{\left\| \omega \right\|^2} + C\sum\limits_{i = 1}^l {({\xi _i} + {\zeta _i})} ] $$ (3) $$ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ \begin{array}{l} yi - [{\omega ^{\rm T}}\varphi (xi) + {\rm{b}}] \le \varepsilon + {\xi _i}\\ {\omega ^{\rm T}}\varphi (xi) + {\rm{b}} - yi \le \varepsilon + {\zeta _i}\\ \xi i, \zeta i \ge 0 \end{array} \right. $$ (4) 通过引入Lagrange乘子α, β, η，定义Lagrange函数的二次规划方程为：
$$ \begin{array}{l} \;\;L(\omega, b, \alpha, \beta) = \frac{1}{2}{\left\| \omega \right\|^2} + C\sum\limits_{i = 1}^l {({\xi _i} + {\zeta _i}) - \sum\limits_{i = 1}^l {{\alpha _i}({\xi _i} + \varepsilon - {y_i} + (\omega \cdot \varphi ({x_i})) + b)} } \\ - \sum\limits_{i = 1}^l {{\beta _i}} ({\zeta _i} + \varepsilon - {y_i} - (\omega \cdot \varphi ({x_i})) - b) - \sum\limits_{i = 1}^l {{\eta _i}({\xi _i} + {\zeta _i})} \end{array} $$ (5) 其中，$\alpha {\rm{, }}\beta {\rm{, }}\eta \ge 0$；xi，yi为模型的输入和输出；ω为权重向量，b为偏值；i=1，2，…，l，l为样本个数；C为惩罚参数，用于控制模型的复杂度和逼近误差；ε主要用于控制误差和模型的泛化能力。其函数的值条件为：
$$ \frac{{\partial L}}{{\partial \omega }} = 0 \to \omega = ({\beta _i} - {\alpha _i}) \cdot \varphi ({x_i}) $$ (6) $$ \frac{{\partial L}}{{\partial b}} = 0 \to \sum\limits_{i = 1}^l {({\beta _i} - {\alpha _i})} = 0 $$ (7) $$ \frac{{\partial L}}{{\partial {\xi _i}}} = 0 \to \gamma - {\alpha _i} - {\eta _i} = 0\;\;\;(i = 1, 2, \cdots, l) $$ (8) $$ \frac{{\partial L}}{{\partial {\zeta _i}}} = 0 \to \gamma - {\beta _i} - {\eta _i} = 0\;\;\;(i = 1, 2, \cdots, l) $$ (9) 解得：
$$ b = {y_i} - \sum\limits_{j = 1}^l {({\alpha _j} - {\beta _j})\; \cdot K({x_i}, {x_j}) - \varepsilon } $$ (10) 或：
$$ b = {y_i} - \sum\limits_{j = 1}^l {({\alpha _j} - {\beta _j}) \cdot K({x_i}, {x_j}) - \varepsilon } $$ (11) 根据这些条件可以得到引入Lagrange函数的二次规划的对偶问题：
$$ \mathop {{\rm{min}}}\limits_{{a_i}, {\beta _i}} \frac{1}{2}\sum\limits_{i = 1}^l {\sum\limits_{j = 1}^l {({\alpha _i} - {\beta _i})({\alpha _j} - {\beta _j})} } \cdot K({x_i}, {x_j}) - \sum\limits_{i = 1}^l {{y_i} \cdot ({\alpha _i} - {\beta _i}) + \varepsilon \sum\limits_{i = 1}^l {({\alpha _i} + {\beta _i})} } $$ (12) 令：
$$ \sum\limits_{i = 1}^l {({\alpha _i} - {\beta _i}) = 0} \;\;\left({{\alpha _i} \ge 0, C \ge {\beta _i}, i = 1, 2, \cdots l} \right) $$ (13) 在求得对偶问题的最优解，在最优解中对应的非零向量为α, β; $\alpha = (\alpha 1, \alpha 2, \cdot \cdot \cdot, \alpha_l)$, $\beta = (\beta 1, \beta 2, \cdot \cdot \cdot, \beta_l)$；进一步就得到该高维特征空间的最优超平面 (即非线性回归方程)：
$$ f(x) = \sum\limits_{i = 1}^l {({\alpha _i} - {\beta _i})} \cdot K({x_i}, {x_j}) + b $$ (14) 核函数为RBF (径向基函数)，采用其高斯形式 (白春华等，2013)：
$$ K(x, x') = {\rm{exp(}} - \frac{{{{\left\| {x - x'} \right\|}^2}}}{{2{\delta ^2}}}{\rm{)}} $$ (15) 在RBF为核函数的SVM模型中，SVM的性能在一定的方面容易受到惩罚参数C和核函数参数δ2的影响，在下文中核函数参数δ2用Γ表示，因此，结合粒子群算法的优点进行全局寻优来不断的优化惩罚参数C和核函数参数，使得预测结果更加准确。
2. 模型的建立
2.1 模型数据的输入
通过查阅资料，收集了唐山地震、丽江地震、汶川地震、海城地震、通海地震、台湾集集地震中的城市桥梁震害情况 (吴昊，2009；郭恩栋等，2014；刘恢先，1986)，根据经验统计法已有的研究成果，且城市桥梁建设广泛采用桩基础，所以模型中不考虑基础类型因素。模型选择影响桥梁震害等级的8个主要因素主要包括地震烈度、场地土类型、地基失效程度、上部结构、墩台高度、支座型式、桥梁跨数和桥梁的建成年代，用以上8个因素作为特征输入向量，并结合城市桥梁的相关特征。由于PSO-SVM模型只能对已量化的数字信息进行处理，但本文所选择的影响桥梁震害的8个因素都是非量化的，所以采用吴昊 (2009)对桥梁震害的影响因素进行量化的方法得到相应的值。城市桥梁主要震害因素和其量化值如表 1。
表 1 震害影响因素指标及量化值Table 1. Quantitative value of disaster factors影响因素 量化值 地震烈度 7度 1.0 8度 1.1 9度 1.2 10度 1.5 场地土类型 Ⅰ类 0.8 Ⅱ、Ⅲ类 1 Ⅳ类 1.2 场地失效程度 无 1.0 轻 1.5 重 1.8 上部结构 简支梁 1.0 连续梁 1.4 墩台高度 ≤5m 1.0 5-10m 1.1 ≥10m 1.2 支座型式 有防落梁措施 1.0 消能支座 1.2 一般支座 1.4 桥梁长度 跨数≤3 1 跨数＞3 1.2 桥梁的建成年代 1987年以前 1.1 1987-2006年 1.0 2006年以后 0.9 2.2 模型数据的输出
根据国内现有桥梁地震破坏等级的分类标准，通常把桥梁震害分为基本完好、轻微破坏、中等破坏、严重破坏和毁坏5个等级 (王再荣等，2010)，各个震害等级下破坏现象的描述如表 2。由于模型只能对已量化的数字信息进行处理，因此把桥梁震害等级的5种情况--基本完好、轻微破坏、中等破坏、严重破坏和毁坏分别对应模型的输出结果为1、2、3、4、5(如表 3)。输出结果的每一个标识对应着一种桥梁的破坏情况。
表 2 桥梁破坏等级划分Table 2. Classification criterion of bridge damage破坏等级 震害描述 基本完好 承重结构完好，桥面无明显变化，只有个别构件轻微损坏，其他构件无损，可正常通行 轻微破坏 桥台、桥面、桥墩、桥拱、桥塔、主梁等的混凝土部件表面出现细裂缝，非承重构件有破坏，桥面伸缩有变化，梁有轻微的移动，腹拱有细微裂缝，拱身有微裂，拱肋与拱波关系处松脱，墩台轻微变位，台背填土下沉等，可照常使用。 中等破坏 桥墩混凝土出现明显裂缝，梁端混凝土出现明显裂缝，支座与梁连接的螺栓部分剪断，梁移动，桥塔结构轻微变形，墩台轻微移动，出现明显裂缝梁，端混凝土脱落，腹拱错位，拱肋、拱波龟裂，墩台微移动或开裂，经适当修复可使用。 严重破坏 桥墩混凝土出现贯通裂缝、剥落，梁、拱出现贯通裂缝或破碎，桥塔结构变形，主要承重构件破坏、断裂，如梁、拱开裂或破碎，墩台滑移、断裂或严重倾斜，承载能力明显降低，必须大修。 毁坏 发生落梁、塌拱、墩台折断等破坏、倒塔，已不能使用，需重建。 表 3 桥梁震害等级标识Table 3. Classification criterion of bridge damage by earthquake桥梁破坏等级 基本完好 轻微破坏 中等破坏 严重破坏 倒毁 标识 1 2 3 4 5 2.3 粒子群优化算法
上文已经确定了影响支持向量机预测的基本因素是惩罚参数C和核函数的宽度，这两个参数的微妙变化都会影响预测结果的精度，本文主要比较用粒子群优化的前后模型预测准确度的变化，通过对结果的比较来研究更为准确的城市桥梁震害预测的模型。通过粒子群算法来寻找最佳的核函数参数和惩罚参数C，使模型的预测结果不断得到优化，相关的步骤的流程图如下：
图 1 PSO-SVM桥梁震害预测模型的构建Figure 1. Flowchart of PSO-SVM construction for seismic damage prediction model of urban bridge2.4 桥梁数据的归一化处理
在利用PSO-SVM模型进行桥梁震害预测时，需要对已量化的训练数据和测试数据进行归一化处理，这样就使得不同类型的数据之间有一定的可比性，同时在一定的程度上也消除了数据之间的量纲差异，使不同类型的桥梁震害影响因子的量化值处于同一个数量级，有利于对数据进行综合评价。
$$ {\overrightarrow x_{ik}} = \frac{{{X_{ik}} - X_k^{\min }}}{{X_k^{\max } - X_k^{\min }}} $$ (16) 公式 (16) 对数据进行线性转换，将桥梁震害数据的量化值转换到[0，1]，${\overrightarrow x _{ik}}$表示第i个样本、第k个因素归一化指标值，Xik表示第i个样本、第k个因素的量化值，$X_k^{\max }$和$X_k^{{\rm{min}}}$分别为k个因素列中的最大值和最小值。
2.5 PSO-SVM的迭代的收敛过程
利用Libsvm工具箱及Matlab软件设置PSO-SVM的初始参数。设粒子的种群s=40，最大迭代次数kmax=300，学习因子c1，c2取值分别为1.2和1.5。图 2可以看出粒子群的适应度在前期的变化的幅度比较大，这样可以保证粒子群算法具有较好的全局寻优能力，避免寻优结果达到局部最优。后期粒子寻优的最佳适应度的变化幅度较小，则表明粒子快速收敛已达到最优。同样粒子群优化的适应度是判定训练样本位置优化好坏的有力标准，优化后的惩罚参数C和Γ分别取值为53.88和0.01，从图 2中可以看出，经过参数优化的支持向量机预测模型具有较好的收敛效果。
3. 实验仿真结果与分析
PSO-SVM预测模型选择123个具有代表性的桥梁样本，其中103个作为训练样本，20个作为测试样本用于仿真检验。借助Matlab及相关软件对20个测试样本进行预测，将模型的预测结果与实际桥梁震害结果进行比较，更能直接地观测实验结果的准确度。相应的实验预测结果在图 3和图 4中进行了详细的描述。从表 4中得知，PSO-SVM模型预测结果只有序号为4、15、18的3座桥梁的震害与实际震害结果不一致，而SVM模型的预测结果有序号为4、6、9、15、18、20的6座桥梁与实际震害结果有差异。
表 4 模型预测结果差异项比较Table 4. Comparison of predicted results from various models预测模型 预测结果差异项序列号 差异项的预测震害指数 差异项的实际震害指数 模型预测精度 SVM 4 3 5 70% 6 3 4 9 2 3 15 2 3 18 2 4 20 3 4 PSO-SVM 4 4 5 85% 15 2 3 18 3 4 从实验的结果来看，PSO-SVM和SVM的预测结果都和桥梁震害的实际结果进行了比较，PSO-SVM的计算结果的精度高于SVM。为使结果更易于清晰可见，特制作表 4来对比2种模型的预测结果。
从表 4可以看出，PSO-SVM模型对桥梁的预测结果明显优于没有被PSO算法优化过的预测模型，同时模型没有出现过拟合现象，从而可以得知PSO-SVM预测模型用于城市桥梁震害预测和评估是切实可行的。
4. 结论
本文通过对比基于SVM和PSO-SVM的桥梁群体震害预测模型对测试桥梁样本的预测结果，结论显示，PSO-SVM模型不仅提高了城市群体桥梁震害预测的准确率，也给出了一种更为科学有效的桥梁震害评估模型，该模型充分利用粒子群算法和支持向量机算法的优点不断优化惩罚参数C和核函数参数δ2，使桥梁震害预测更准确。
但是，本文所提出的PSO-SVM桥梁群体震害评估模型还存在一定的不足之处：① PSO-SVM的桥梁震害模型的预测结果是相对准确的，但是其计算时间较长，不如SVM模型省时；② 模型训练样本和测试样本都基于小样本系统，没有经过较多样本的检验与测试。
-
图 2 50kPa动应力下试样残余应变与振次关系曲线
Figure 2. Relationship of residual strain and cyclic number under 50kPa
图 3 60kPa动应力下试样残余应变与振次关系曲线
Figure 3. Relationship of residual strain and cyclic number under 60kPa
表 1 天津软土的邓肯参数
Table 1. Duncan parameters of soft soil in Tianjin
土类 Ks/kPa Ns 摩擦角/° 粘聚力/kPa 破坏比 淤泥质土 1237 0.465 12 20 0.478 淤泥质粉质粘土 2930 0.39 12 44 0.687 
下载: 导出CSV
表 2 50kPa动应力下各组拟合成果
Table 2. Fitting result of residual strain under 50kPa
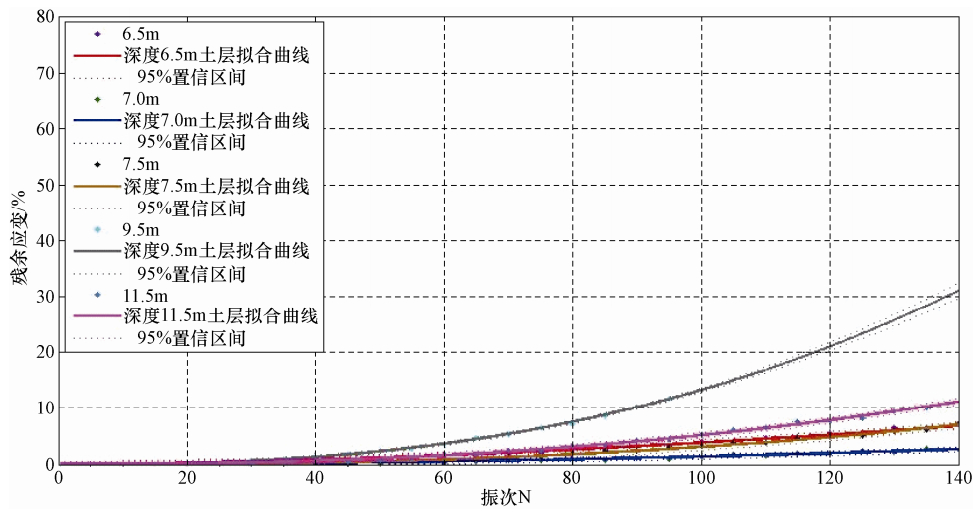
试样深度/m 拟合参数 相关系数 A b 6.5 0.0014 1.72 0.9941 7.0 0.00018 1.95 0.987 7.5 0.000035 2.47 0.997 9.5 0.00010 2.53 0.9987 11.5 0.00010 2.31 0.995
下载: 导出CSV
表 3 60kPa动应力下各组拟合成果
Table 3. Fitting result of residual strain under 60kPa
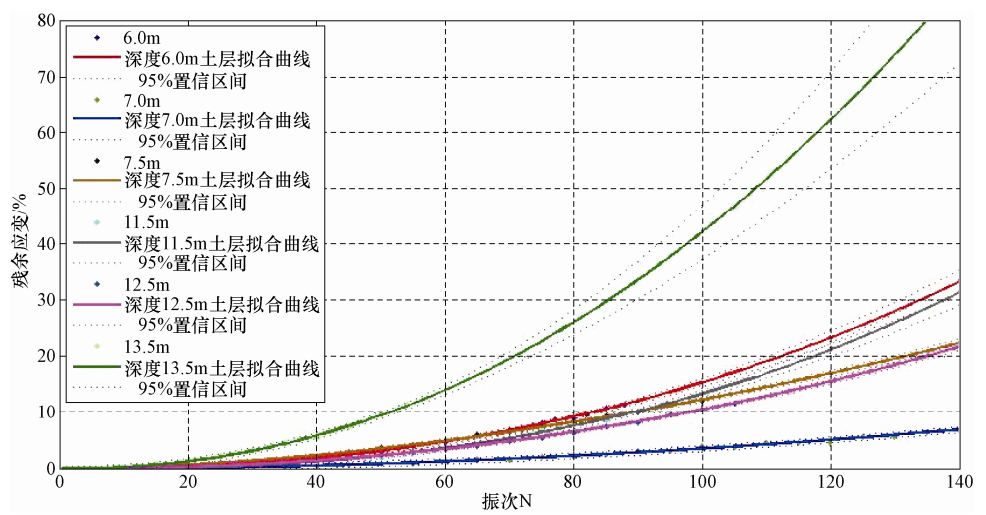
试样深度/m 拟合参数 相关系数 A b 6.0 0.0040 2.28 0.9975 7.0 0.00040 1.96 0.9949 7.5 0.0040 1.77 0.9985 11.5 0.00010 2.52 0.995 12.5 0.00060 2.142 0.9988 13.5 0.0020 2.14 0.997
下载: 导出CSV
表 4 不同震级下等效振动次数
Table 4. Equivalent vibration frequency under different magnitude
震级 6.5 7 7.5 8 振次 8 12 20 30
下载: 导出CSV
表 5 天津地区软土残余应变
Table 5. Residual strain of soft soil in Tianjin
序号 深度 层厚 土类 7.5级地震影响下残余应变 8级地震影响下残余应变 1 4.7 4.7 填土 - - 2 5.5 0.8 填土 - - 3 8.3 2.8 淤粉 0.01 0.2 4 9 0.7 粉粘 0.1 0.3 5 12 3 淤粘 0.1 0.3 6 15.8 3.8 淤粘 0.2 0.35 7 17.5 1.7 粉粘 - - 8 20 2.5 粉粘 - -
下载: 导出CSV
表 6 土层震前模量
Table 6. Soil modulus before earthquake
序号 深度/m 层厚/m 土类 大主应力/kPa 小主应力/kPa 震前模量/kPa 1 4.7 4.7 杂填土 42 28 9571 2 5.5 0.8 素填土 50 34 18103 3 8.3 2.8 淤粉粘 76 50 14632 4 9 0.7 粉粘 81 54 13723 5 12 3 淤粘 103 69 14428 6 15.8 3.8 淤粘 131 88 15186 7 17.5 1.7 粉粘 147 98 16207 8 20 2.5 粉粘 169 113 14232
下载: 导出CSV
表 7 土层震后模量
Table 7. Soil modulus after earthquake
序号 深度/m 层厚/m 土类 震前模量/kPa 7.5级地震影响下割线模量/kPa 8级地震影响下割线模量/kPa 7.5级地震影响下软化模量/kPa 8级地震影响下软化模量/kPa 1 4.7 4.7 杂填土 9571 - 9571 9571 9571 2 5.5 0.8 素填土 18103 - 18103 18103 18103 3 8.3 2.8 淤粉粘 14632 251667 14632 13828 6765 4 9 0.7 粉粘 13723 27033 13723 9103 5439 5 12 3 淤粘 14428 34433 14428 10168 6392 6 15.8 3.8 淤粘 15186 21903 15186 8968 6861 7 17.5 1.7 粉粘 16207 - 16207 16207 16207 8 20 2.5 粉粘 14232 - 14232 14232 14232
下载: 导出CSV
表 8 地震影响下自由地表震陷
Table 8. Seismic settlement of free ground under earthquake motion
序号 深度/m 层厚/m 土类 7.5级地震影响下各层震陷量/m 7.5级地震影响下总沉震陷量/cm 8级地震影响下各层震陷量/m 8级地震影响下总震陷量/m 1 4.7 4.7 填土 - 4.9 - 12.9 2 5.5 0.8 填土 - - 3 8.3 2.8 淤粉 0.001 0.025 4 9 0.7 粉粘 0.003 0.009 5 12 3 淤粘 0.013 0.039 6 15.8 3.8 淤粘 0.032 0.056 7 17.5 1.7 粉粘 - - 8 20 2.5 粉粘 - -
下载: 导出CSV
表 9 不考虑模量软化的自由场地沉降量
Table 9. Free ground settlement without consideration of soften model
序号 深度/m 层厚/m 土类 竖向应力/kPa 动应力/kPa 震前模量/kPa 应变值/% 沉降值/cm 1 4.7 4.7 杂填土 42.3 20.6 9571 0.007 20 2 5.5 0.8 素填土 50.3 24.2 18103 0.004 3 8.3 2.8 淤粉粘 75.5 34.9 14632 0.008 4 9 0.7 粉粘 81.1 37.1 13723 0.009 5 12 3 淤粘 103.3 45.1 14428 0.010 6 15.8 3.8 淤粘 131.42 54.0 15186 0.012 7 17.5 1.7 粉粘 146.72 58.5 16207 0.013 8 20 2.5 粉粘 169.22 64.6 14232 0.016
下载: 导出CSV
表 10 天津滨海地区自由场地软土震陷量修正系数
Table 10. The settlement correction coefficient of free soft soil site in Tianjin
地面峰值加速度/g 震级/M 修正系数C 0.25 7.5 0.2 8 0.6 0.4 7.5 0.25 8 0.5
下载: 导出CSV
-
陈国兴, 李方明, 从卫民, 2004.多层建筑物地基震陷的简化计算方法及其影响因素分析.防灾减灾工程学报, 24(1):47-52. http://www.cnki.com.cn/Article/CJFDTOTAL-DZXK200401008.htm 陈建峰, 俞松波, 叶铁锋等, 2008.软土地基加筋石灰土路堤离心模型试验研究.岩石力学与工程学报, 27(2):287-293. http://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200802012.htm 刘恢先, 1986.唐山大地震震害-第二册.北京:地震出版社. 江席苗, 2009. 汶川地震地基基础震害调查研究. 上海: 同济大学. 李冬, 陈培雄, 吕小飞等, 2011.软土地震震陷研究现状综述.工程抗震与加固改造, 33(2):130-135. http://youxian.cnki.com.cn/yxdetail.aspx?filename=SCSA201704303&dbname=CJFDPREP 孟上九, 袁晓铭, 孙锐, 2002.建筑物不均匀震陷机理的振动台实验研究.岩土工程学报, 24(6):747-751. http://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200206016.htm 吴跃东, 2008. 软土震陷计算方法及影响研究. 南京: 河海大学. 王建华, 要明伦, 1993.饱和软粘土振动弱化特性的研究.水利学报, 12:37-43. doi: 10.3321/j.issn:0559-9350.1993.06.006 谢君斐, 石兆吉, 郁寿松等, 1988.液化危害性分析.地震工程与工程振动, 8(1):61-77. http://www.cnki.com.cn/Article/CJFDTOTAL-DGGC198404006.htm 谢君斐, 石兆吉, 1981.神头电厂地基震陷的初步分析.中国科学院工程力学研究所. 杨石红, 刘静蓉, 刘金珠等, 1997.软弱地基土层震陷简化计算方法研究.世界地震工程, 13(2):53-61. http://www.cnki.com.cn/Article/CJFDTOTAL-SJDC702.007.htm 郁寿松, 石兆吉, 1989.土壤震陷试验研究.岩土工程学报, 11(4):35-44. http://www.cnki.com.cn/Article/CJFDTOTAL-YTGC198904004.htm 中国科学院工程力学研究所, 1979.海城地震震害.北京:地震出版社. 张建毅, 张宇东, 徐国栋, 王强, 2012.软土震陷判别方法分析及工程应用.世界地震工程, 28(3):53-59. http://www.cnki.com.cn/Article/CJFDTOTAL-SJDC201203012.htm 周健, 蔡宏英, 许朝阳, 2000.软粘土地基震陷分析.工程抗震, (1):40-42, 39. http://www.cnki.com.cn/Article/CJFDTOTAL-GCKZ200001011.htm Lee K. L., 1974. Seismic Permanent Deformation in Earth Dams. School of Engineering and Applied Science, University of California, Los Angeles, California, December. Monismith C. L., Ogawa N., Freeme C. R., 1975. Permanent deformation characteristics of subgrade soils due to repeated loading. Transp. Res. Rec. No.537. Transportation Research Board. Washington D.C.:1-17. https://trid.trb.org/view.aspx?id=511499 Narikawa M., Ohshima Y., Nishimura I., et al., 1999. Settlement and seismic behavior of florting foundation on thick cohesive strata. In:Seco e Pointo, ed. Earthquake Geotechnical Engineering. Rotterdam:A A Balkema.421-426. Seed H. B. and Clarence K. C., 1966. Clay Strongth under Earthquake loading Condition, Journal of the Soil Mechanics and Foundation Division, ASCE, 1992, SMZ, March. -
下载:
点击查看大图
计量
- 文章访问数: 149
- HTML全文浏览量: 19
- PDF下载量: 11
- 被引次数: 0
